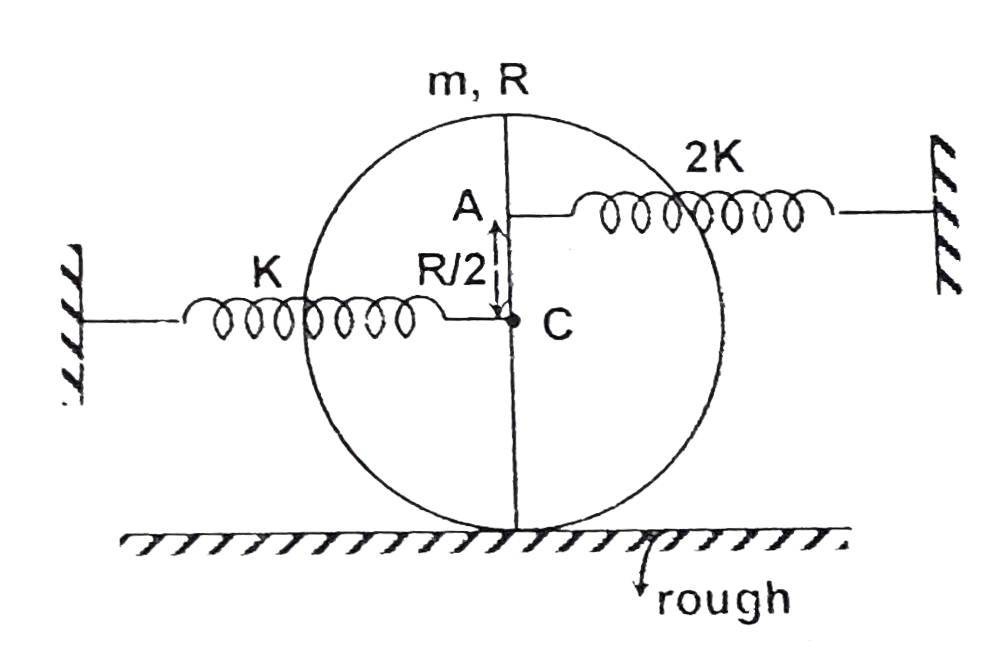
A uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and $2 k$ at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).

A

$2 π \sqrt{\frac{5 m}{7 k}}$

B

$2 π \sqrt{\frac{3 m}{7 k}}$

C

$2 π \sqrt{\frac{5 m}{11 k}}$

D

$2 π \sqrt{\frac{3 m}{11 k}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$\frac{3 m R^{2}}{2} \frac{d^{2} θ}{{d t}^{2}} = - k R^{2} θ - 3 k R θ (\frac{3 R}{2})$
$\frac{3 m R^{2}}{2} \frac{d^{2} θ}{{d t}^{2}} = - \frac{11 k R^{2} θ}{2}$
$\frac{d^{2} θ}{{d t}^{2}} = - (\frac{11 K}{3 m}) θ$
$∴$ Time Period, $T = 2 π \sqrt{\frac{3 m}{11 k}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

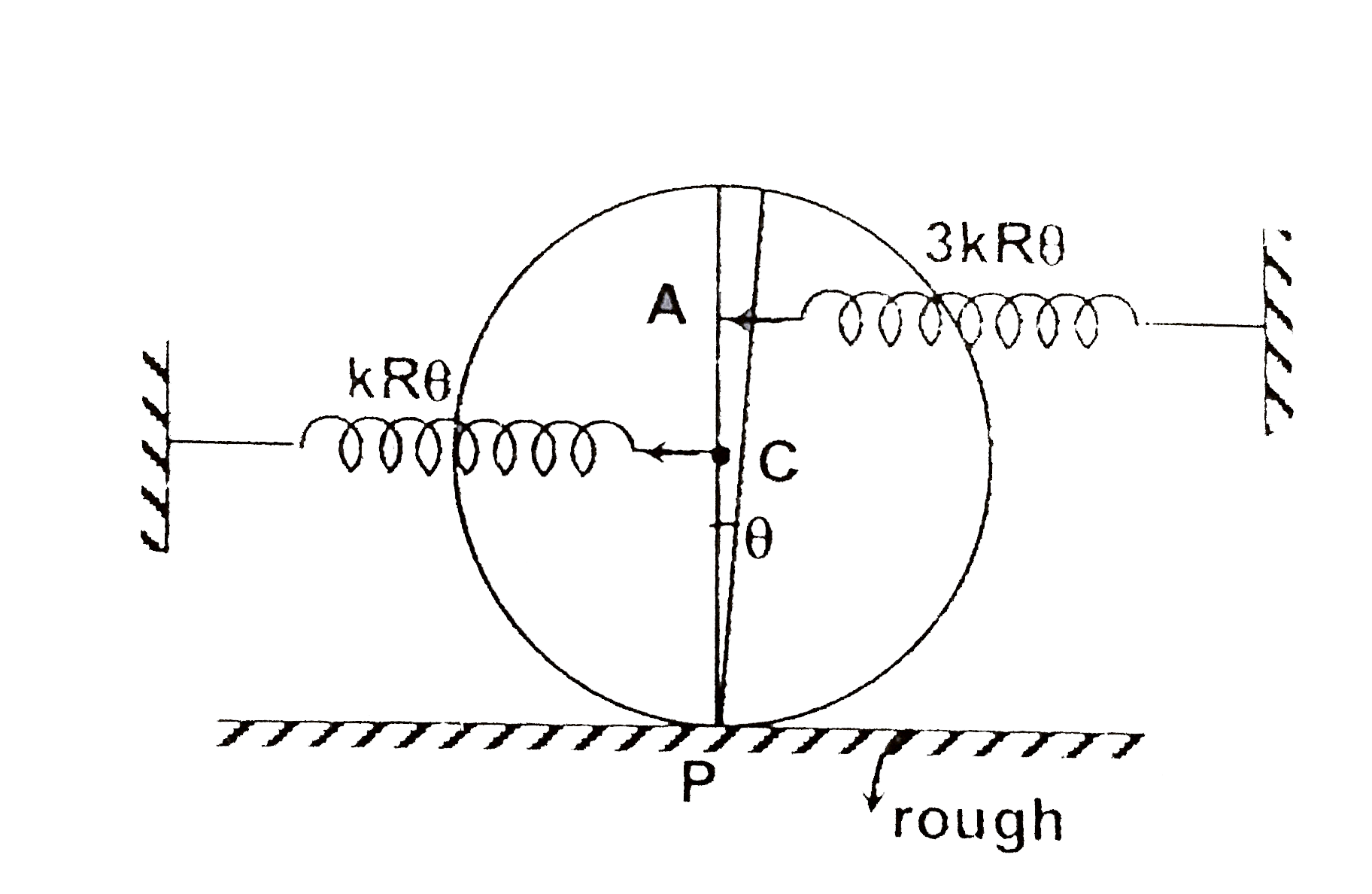
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A disc of mass $m$ and radius $r$ placed on a routh horizontal surface. A cue of mass $m$ hits the disc at a height $h$ from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
A $h < \frac{r}{3}$
B $h = \frac{r}{2}$
C $h > \frac{r}{2}$
D $h \geq \frac{r}{2}$
Question 2 - Select One
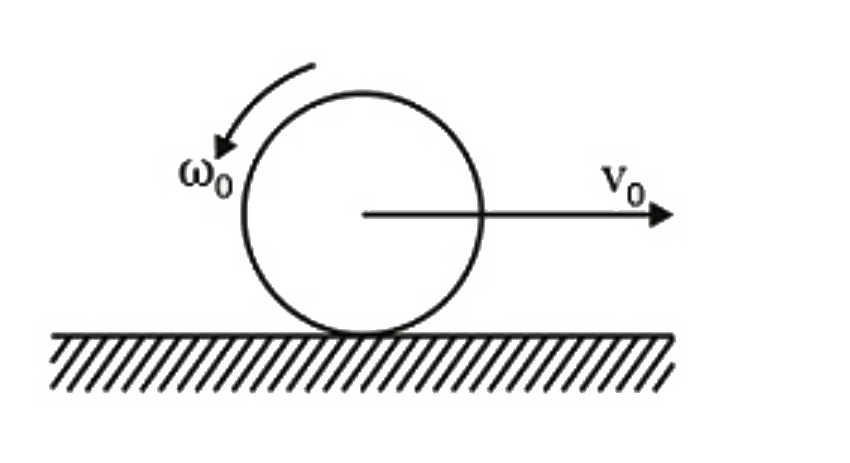
A uniform circular disc of radius $r$ is placed on a rough horizontal surface and given a linear velocity $v_{0}$ and angular velocity $ω_{0}$ as shown. The disc comes to rest after moving some distance to the right. It follows that

A $3 v_{0} = 2 ω_{0} r$
B $2 v_{0} = ω_{0} r$
C $v_{0} = ω_{0} r$
D $2 v_{0} = 3 ω_{0} r$
Question 3 - Select One
A uniform circular disc of mass $M$ and radius $R$ rolls without slipping on a horizontal surface. If the velocity of its centre is $v_{0}$ , then the total angular momentum of the disc about a fixed point $P$ at a height $(3 R) / 2$ above the centre $C$ .

Aincreases continuously as the disc moves away
Bdecreases continuously as the disc moves away
Cis always equal to $2 M R v_{0}$
Dis always equal to $M R v_{0}$

FIITJEE-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile