The end 'A' of a uniform rod AB of length 'l' touches a horizontal smooth fixed surface. Initially the rod makes an angle of 30∘ with the vertical. Find the magnitude of displacement of the end B just before it touches the ground after the rod is released.
The correct Answer is:√13l4
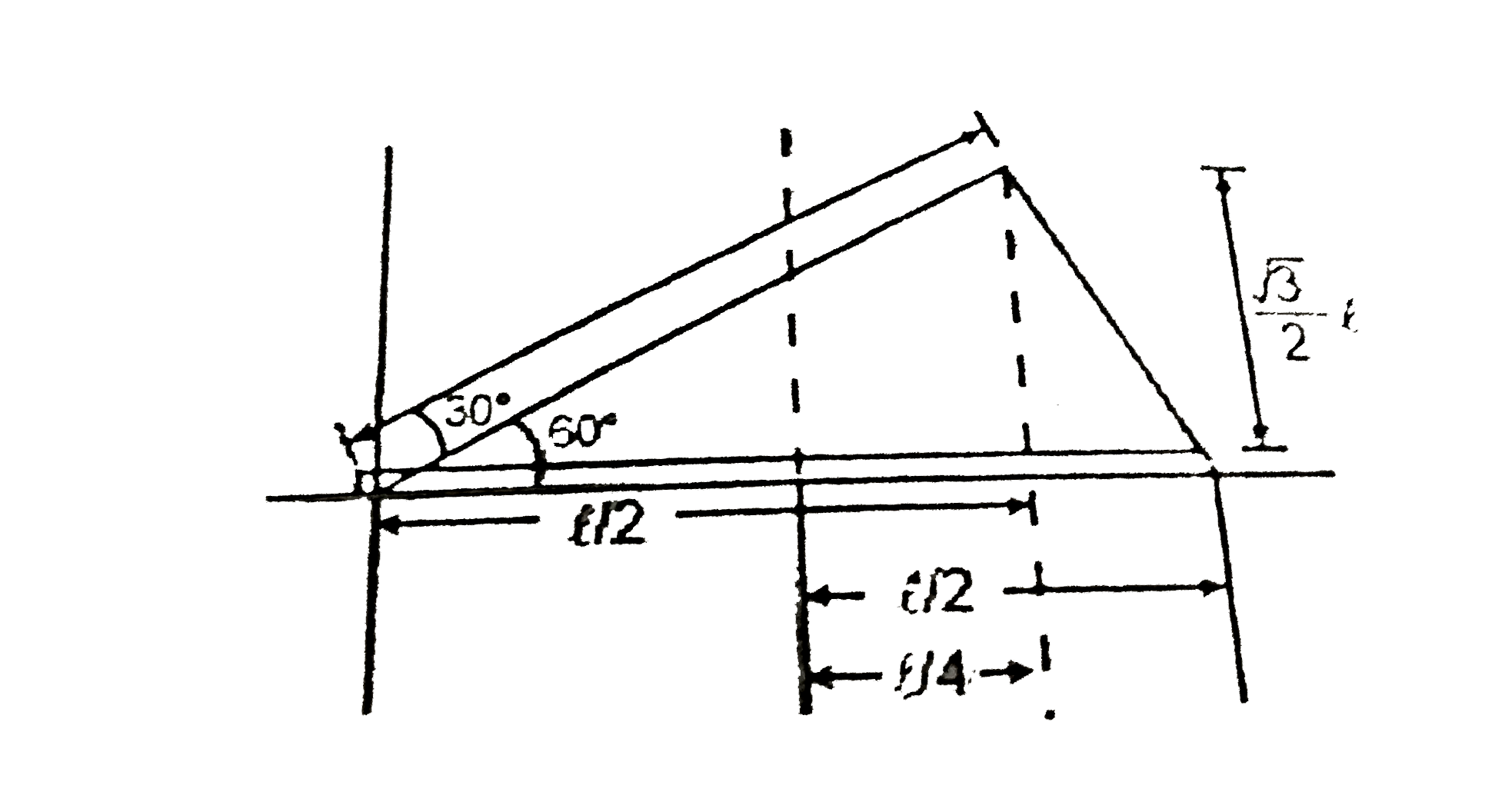
Displacement =√34l2+l216
=12√3+14=√13l4
Alternate solution
Initially the rod is at rest
∴Ucm or rod =0
All forces on rod, acti in vertical direction. Hence acceleration of centre of mass is vertically downwards.
∴ centre of mass of rod moves vertically downwards.
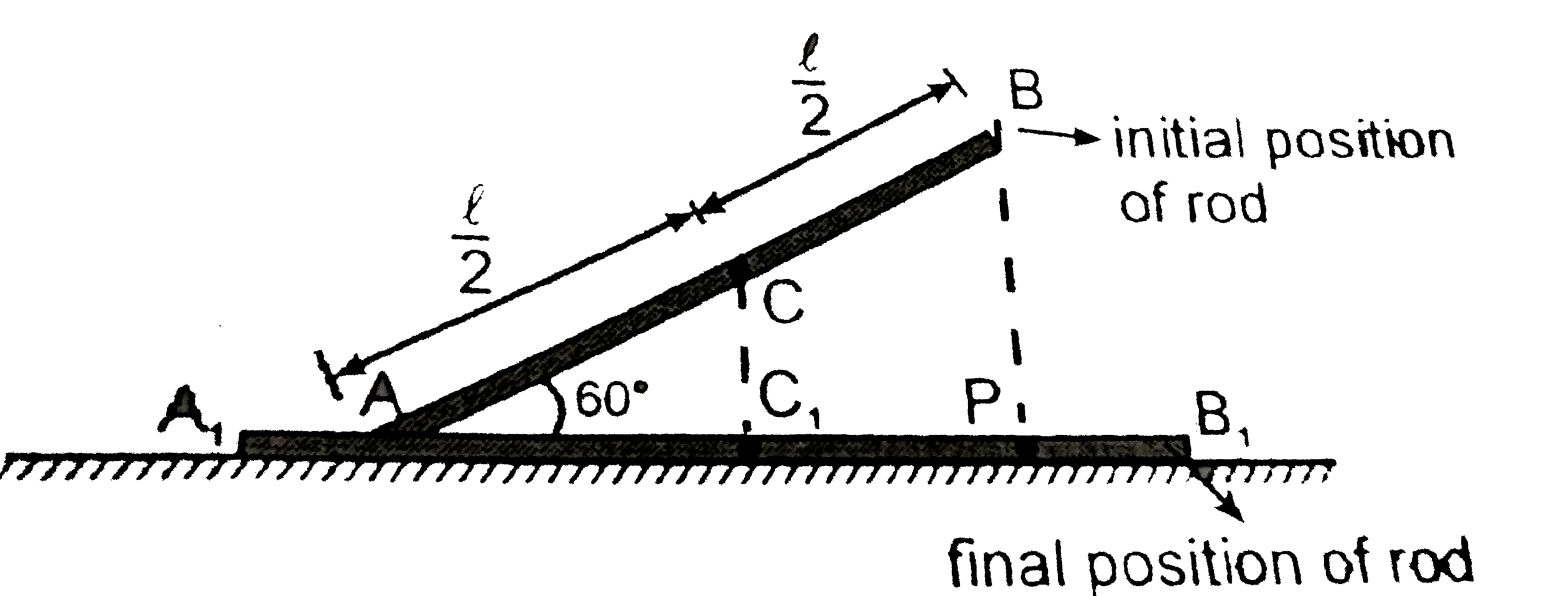
BP=lsin60∘=√32l,C1P=l2cos60∘
∴PB1=B1C1−C1P=l2(1−cos60∘)=l4
∴Displacement of end B is BB1
=√BP2+PB22=
⎷(√32l)2+(l4)2=√13l4
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 548videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 558videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 527videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
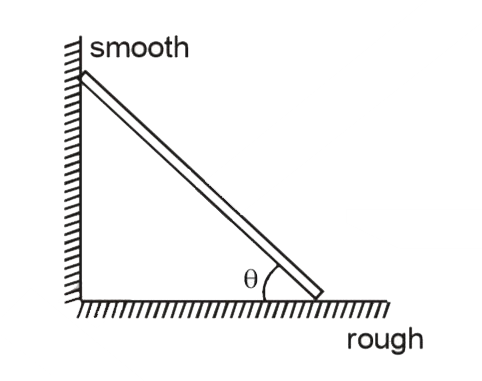
A stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
 View Solution
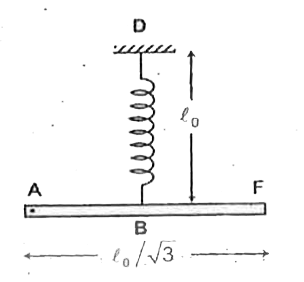
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of length 2a is held with one end resulting on a smooth horizontal table makin an angle α with the vertical. When the rod is released,
Aits center of mass moves vertically downwards on a straight lineBIts center of mass remains in restCthe rod rotates about a vertical axisDBoth a and c are correct - Question 2 - Select One
A uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be
A4mg/7B5mg/9C2mg/5DNone of these - Question 3 - Select One
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpml
A uniform rod of length l is held vertically on a horizontal floor fixing its lower end, the rod is allowed to fall onto the ground. Find (i) its angular velocity at that instant of reaching the ground (ii) The linear velocity with which the tip of rod hits the floor.
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod pivoted at its upper end hangs vertically. It is displaced through anangle of 60∘ and then released. Find the magnitude of the force acting on a particle of mass dm at the tip of the rod when the rod makes an angle of 37∘ with the vertical.
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 View Solution
View Solution

