The circular vertical section of the fixed track shown is smooth with radius and the horizontal straight section is rough with . A block of mass is placed at point and given a horizontal velocity of towards the spring. Distance and maximum compression in the spring is during the motion

The force constant of the spring is
The velcoity with which block returns to point is
At point its velocity will be
At point , the normal reaction on the block is less than
The correct Answer is:A, B, C

.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 54
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:DPP 55
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 52
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
In the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.

View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0Two blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is
 A5cmB2cmC3cmD4cm
A5cmB2cmC3cmD4cmA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
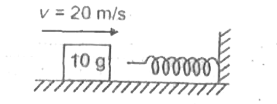 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43m
2 mass of block 2 kg & 4 kg are attached to a stiffness spring 100 N/m. 2 kg mass is given velocity 2 m/s & 4 kg to 4 m/s in same direction. Find maximum elongation in the spring during the motion of two blocks.
View SolutionA body of mass 5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface collides with a nearly weightless spring of force constant k = 5 N/m. The maximum compression of the spring would be

View SolutionA block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
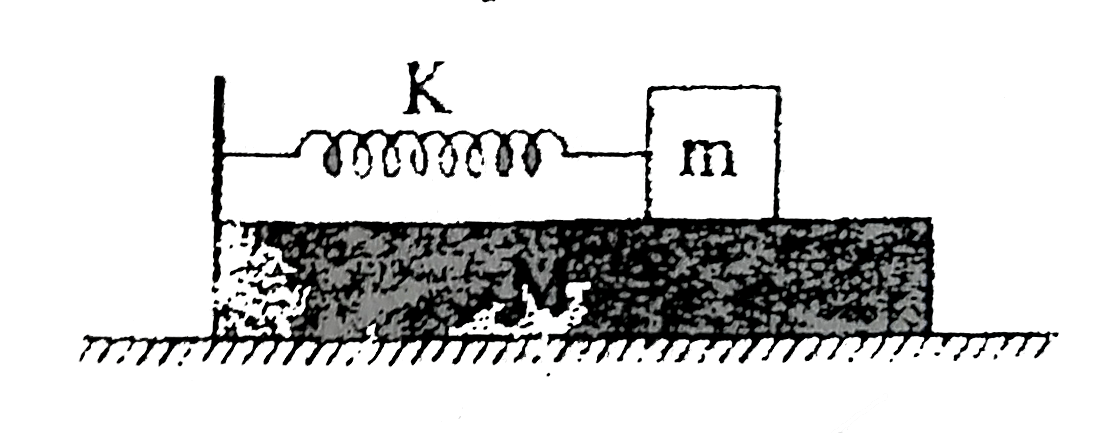
View SolutionA mass of 0.5kg moving with a speed of 1.5m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50N/m The maximum compression of the spring would be.
View SolutionA block of mass 1kg kept over a smooth surface is given velocity 2m/s towards a spring of spring constant 1N/m at a distance of 10m. Find after what time block will be passing through P again
 .
.
View Solution