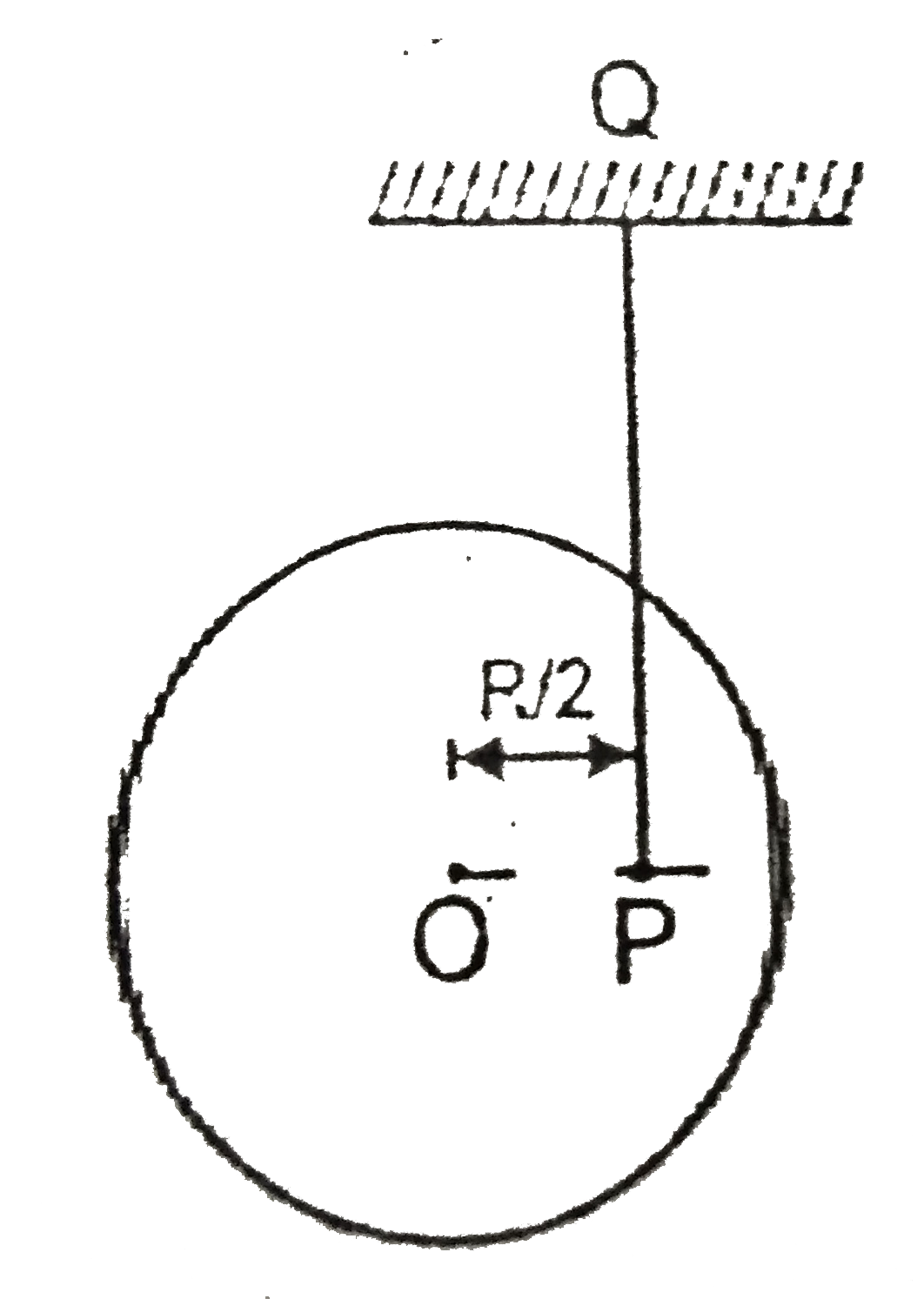
A uniform disc of mass M and radius R is released from the shown position . PQ is s tring , OP is a horizontal line , O is the centre of the disc and distance OP is R/2. The tension in the string just after the disc is released will be :
Mg2
Mg3
2Mg3
none of these
The correct Answer is:C
(C)
Applying Newton's law on the centre of mass O
Mg−T=ma{a= acceleration of centre of mass }
τ=Iα, about centre of mass
T=R2=MR22.α
Also a=R2α from above equations T=2mg3
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 664videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 672videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 645videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
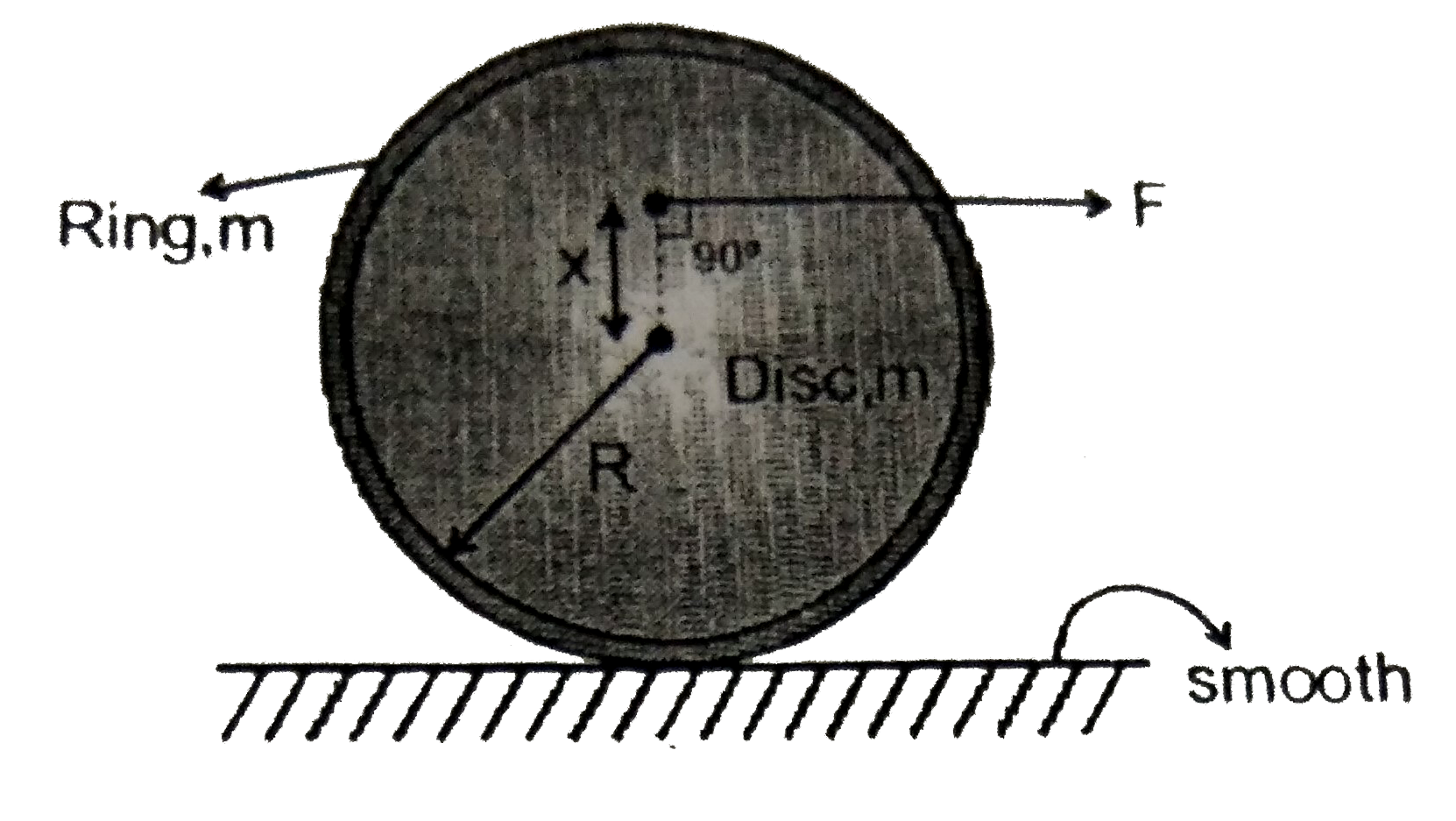
A ring and a disc of same mass m and same radius R are joinged concentrically. This system is placed on a smooth plane with the common axis parallel to the plane as shown in figure. A horizontal force F is applied on the system at a point which is at a distance x from the centre. The value of x so that it starts pure rolling is
08:59View SolutionThere are four arrangements of a solid cylinder and a plank as shown in the figures. Some surfaces are smooth and some are rough as indicated . There is no slipping at each rough surface. The plank and / or centre of cylinder are given a horizontal constant velocity as shown in each of the situations. Usinn this information fill in the blanks.
The speed of center of mass of the cylinder is ..........................
(ii) ,
The angular velocity of the cylinder is ........................
(iii),(RESPHYDPP04_XIE01537_Q03.png width=80%>Thespeedofcenterofmassofthecyl∈dris................<br>(iv),<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_PHY_DPP_04_XI_E01_537_Q04.pngwh=80%mx-autosty≤=background:white;>Theanga––rvelocityofthecyl∈deris.............<br>(a) V<br>(b) V//R<br>(c) 2V//R<br>(d) 4V//R<br>(e)ca∩otbedeterminedomthegiven∈formation<br>(f) Zero.04:28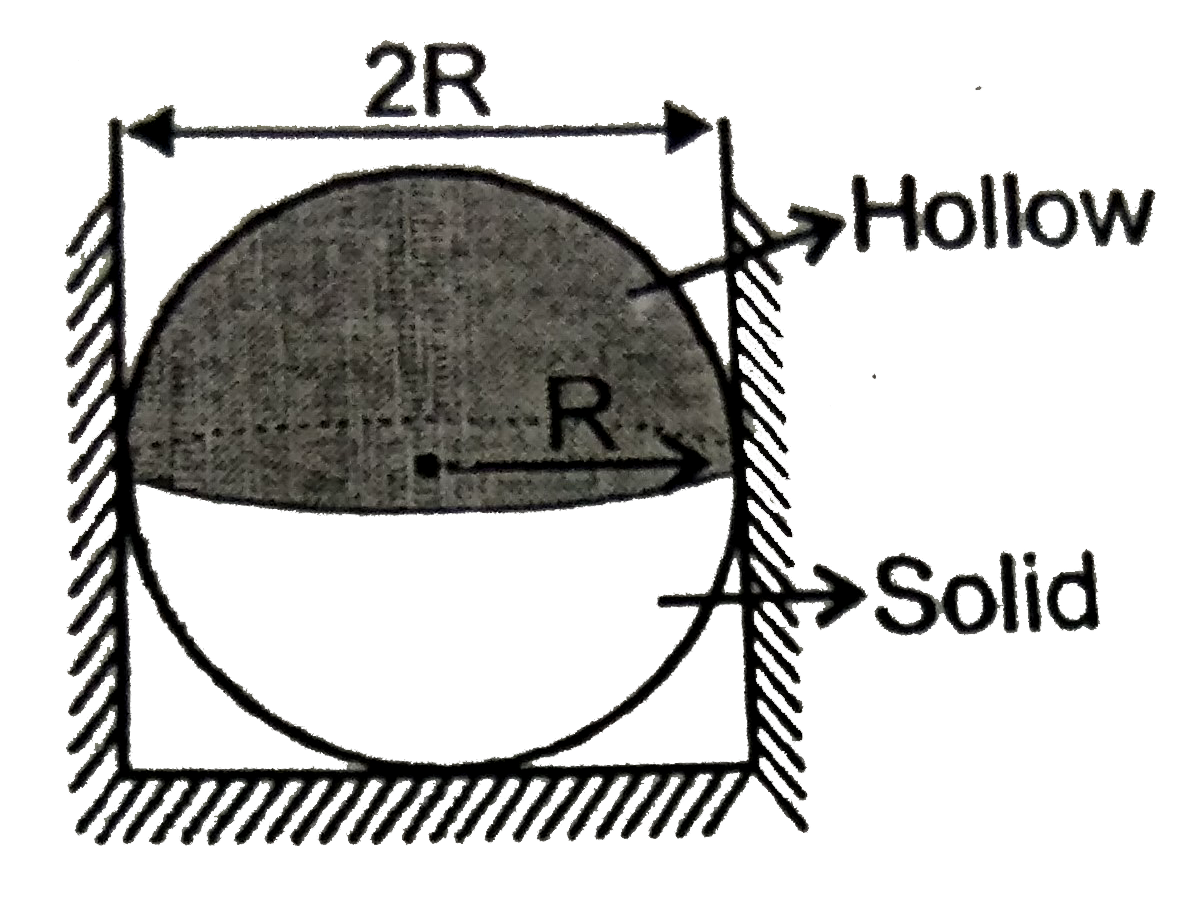View SolutionA compound sphere is made by joining a hemispherical shell and a solid hemisphere of same radius R and same mass as shown in figure. This system is kept between two smooth parallel walls and a smooth floor with the hollow hemisphere on the top as shown in figure. The maximum angular velocity of the compound shere when the system is slightly disturbed is ( all surfaces are smooth )
05:12View SolutionSpecific resistance of a wire depends on its
13:18View SolutionA wire loaded by a weight of density 7.6gcm−3 is found to measure 90cm. On immersing the weight in water, the length decreases by 0.18cm. Find the original length of wire.
02:28View SolutionA uniform circular disc has radius R and mass m . A particle, also of mass m , if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R//4 from the centre C of the disc. The line AC is perpendicular to PQ . Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
04:34View SolutionGiven a uniform disc of mass M and radius R . A small disc of radius R//2 is cut from this disc in such a way that the distance between the centres of the two discs is R//2 . Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
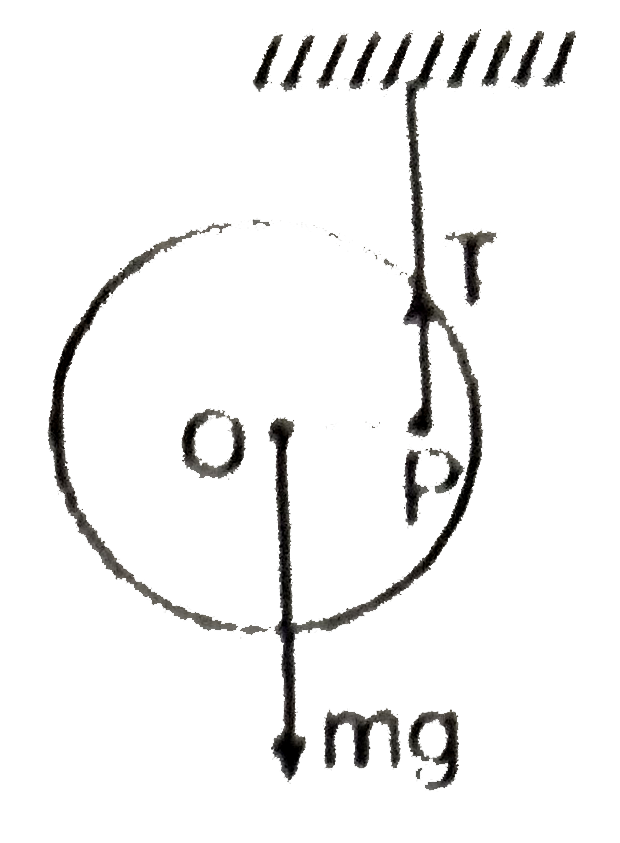
View SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information The angular velocity of the disc in the above described case is
08:59View SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information Reaction force exerted by the hinge on the disc at this instant is
03:03View SolutionA disc of a mass M and radius R can rotate freely in vertical plane about a horizontal axis at O. Distant r from the centre of disc as shown in the figure. The disc is released from rest in the shown position.
The angular acceleration of disc when OC rotates by an angles of 37∘ isView SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius (R)/(2) is removed from it. Then choose the correct option(s)
01:29View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
08:15View Solution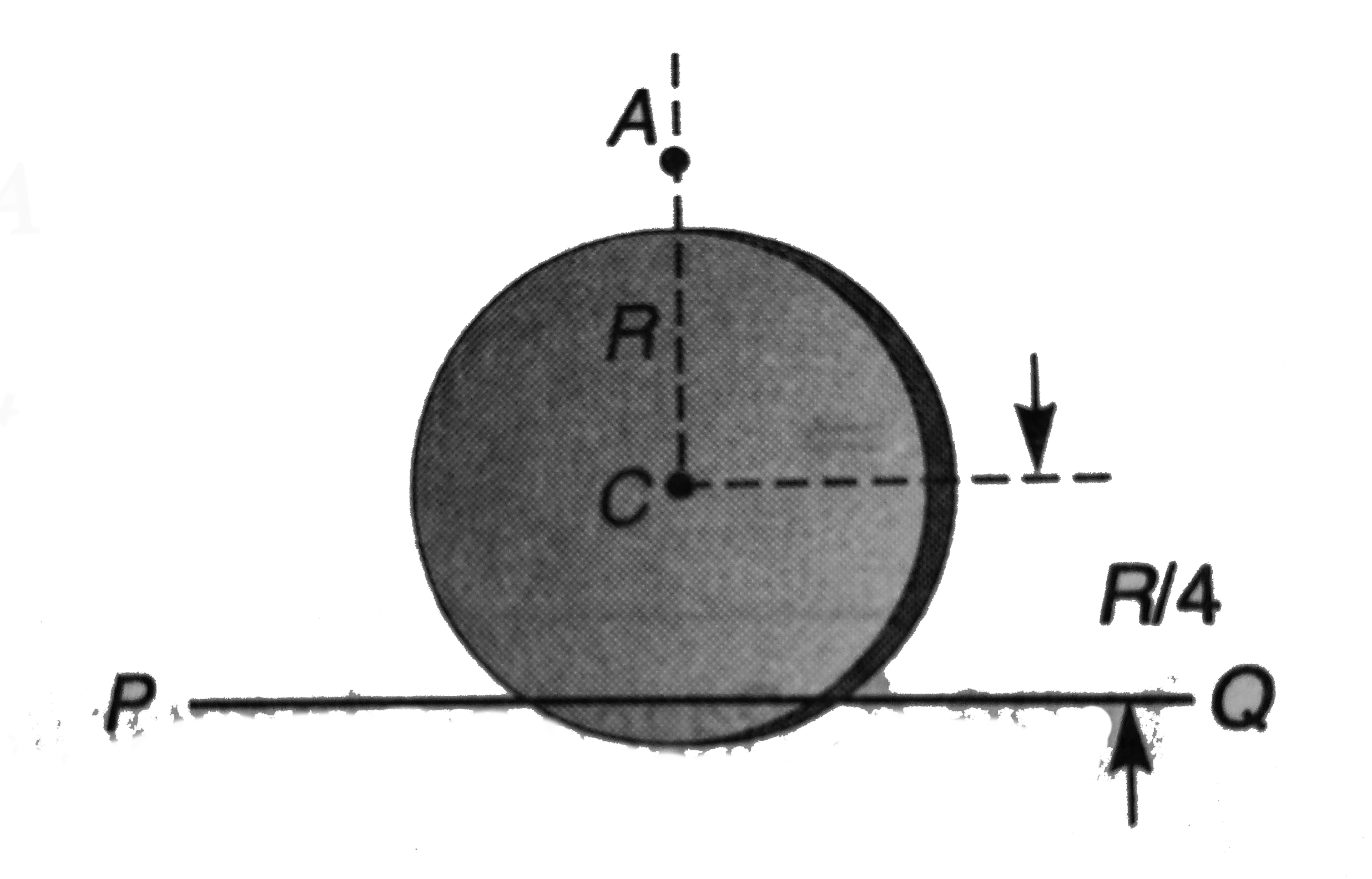
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.04:54View SolutionThe moment of Inertia of a uniform semicircular disc of mass M and radius 'r' about a line perpendicular to the plane of the disc through the centre is :
03:13View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
02:14View Solution