A disc is in the condition of pure rolling on the horizontal surface. The velocity of center of mass isV0 If radius of disc is R then the speed of point P is (OP=R3)
1√3
3√3
√133
13
To solve the problem, we need to determine the speed of point P on the disc when the center of mass is moving with a velocity V0 and the distance from the center of the disc to point P is OP=R3.
1. Understanding Pure Rolling:
In pure rolling motion, the point of contact of the disc with the surface has zero velocity relative to the surface. The center of mass moves with a velocity V0 and the disc rotates about its center.
2. Relating Linear and Angular Velocity:
The relationship between the linear velocity V0 of the center of mass and the angular velocity ω of the disc is given by:
V0=Rω
where R is the radius of the disc.
3. Finding the Speed of Point P:
Point P is located at a distance of R3 from the center of the disc. The speed of any point on the disc can be found using the formula:
vP=V0+(speed due to rotation)
The speed due to rotation at point P is given by:
vrotation=ω⋅r
where r is the distance from the center to point P. Here, r=R3.
4. Substituting for ω:
From the earlier relationship, we can express ω as:
ω=V0R
Now substituting this into the speed due to rotation:
vrotation=(V0R)⋅(R3)=V03
5. Total Speed of Point P:
Now, we can find the total speed of point P:
vP=V0+V03=V0(1+13)=V0⋅43
Thus, the speed of point P is:
vP=4V03
In pure rolling motion, the point of contact of the disc with the surface has zero velocity relative to the surface. The center of mass moves with a velocity V0 and the disc rotates about its center.
The relationship between the linear velocity V0 of the center of mass and the angular velocity ω of the disc is given by:
V0=Rω
where R is the radius of the disc.
Point P is located at a distance of R3 from the center of the disc. The speed of any point on the disc can be found using the formula:
vP=V0+(speed due to rotation)
The speed due to rotation at point P is given by:
vrotation=ω⋅r
where r is the distance from the center to point P. Here, r=R3.
From the earlier relationship, we can express ω as:
ω=V0R
Now substituting this into the speed due to rotation:
vrotation=(V0R)⋅(R3)=V03
Now, we can find the total speed of point P:
vP=V0+V03=V0(1+13)=V0⋅43
vP=4V03
Topper's Solved these Questions
Similar Questions
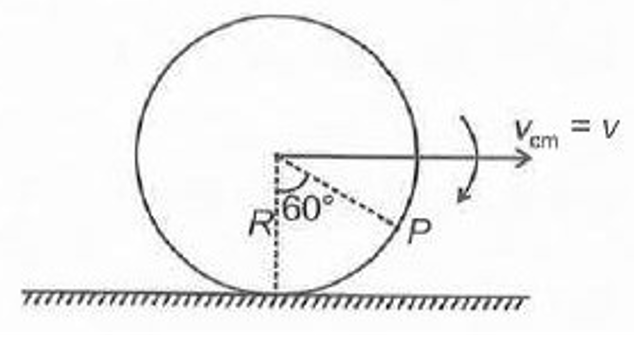
A cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA uniform disc of radius R is in pure rolling on a fixed horizontal surface with constant speed v0 as shown in the figure. For what value of θ, speed of point P will be v02√(5+2√3) ? (OP= R/2 and O is the centre of disc)

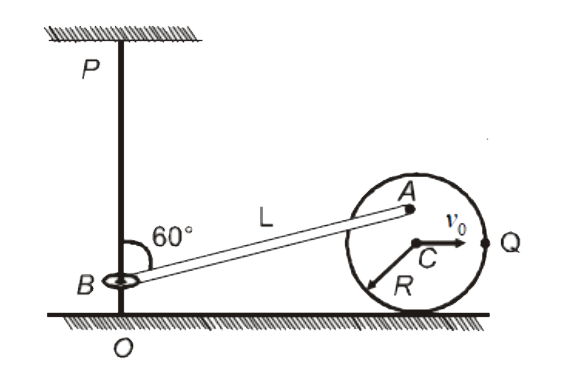
View SolutionA smooth rod OP is fixed vertically. A disc of mass m and radius R is rolling without slipping at the given instant on a rough horizontal surface as shown. Velocity of centre of mass C of disc is v0. A rod AB of length L is connected with disc at A, R/2 distance vertically up from centre of disc with pin joint (about which it can rotate freely), other end of the rod is attached to a small smooth ring B, which can move freely over rod OP. At an instant rod AB makes an angle 60∘ with the vertical. The velocity of ring on the vertical rod at this instant is.
View SolutionIn case of pure rolling what will be velocity of point A of the ring of radius R ?

View SolutionA disc of radius R is rolling without sliding on a horizontal surface with a velocity of center of mass v and angular velocity ω in a uniform magnetic field B which is perpendicular to the plane of the disc as shown in Fig. 3.179. O is the center of the disc and P,Q,R,andS are the four points on the disc. Which of the following statements is true?

View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View SolutionA disc is in pure rolling motion on a rough horizontal surface. It enters into a frictionless horizontal surface. What will happen?
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View Solution
