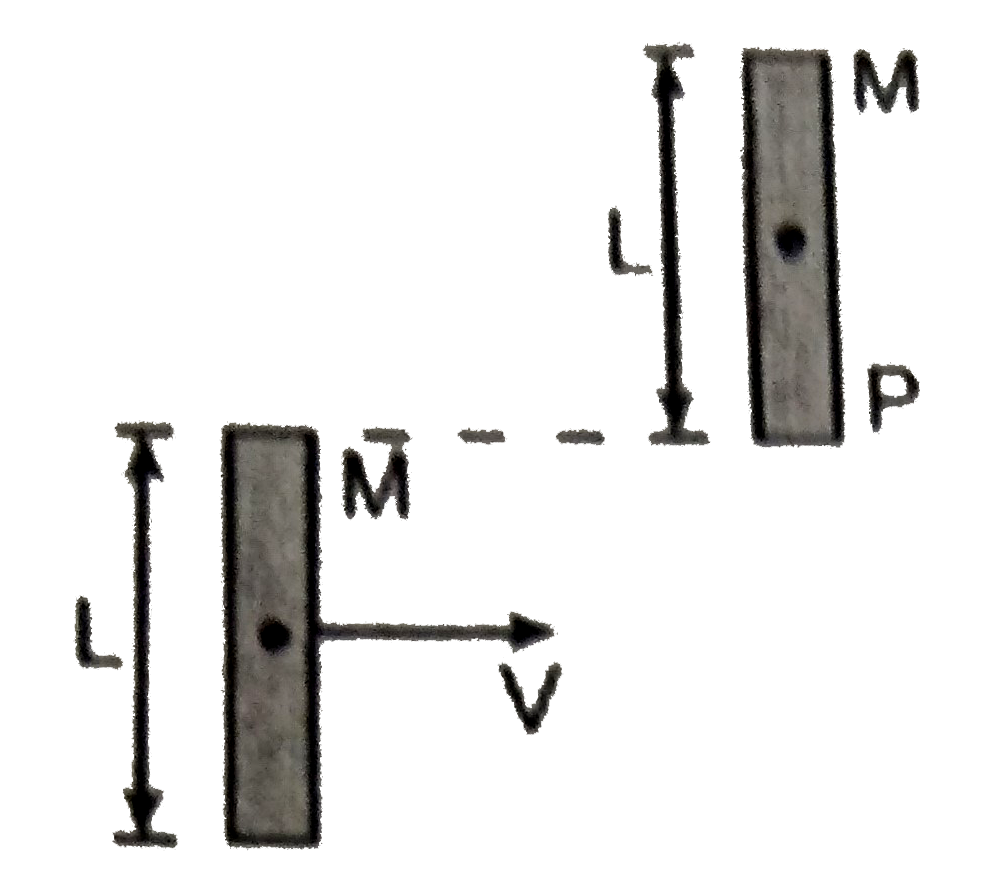
A bar of mass M and length L is in pure traslatory motion with its of mass velocity V . It collides with and sticks to a second identical bar which is initially at rest . ( Assume that it bocomes one composite bar of length 2L). The angular velocity of the composite bar will be
34VL clockwise
43VLL clockwise
34VL counterclockwise
VL counterclockwise
The correct Answer is:C
Cons. Of ang. Momentum about P gives
MVL2=(2M)(2L)212ω
V2=2Lω3
ω=3V4L, counterclockwise Ans.(C)
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 664videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 672videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 645videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
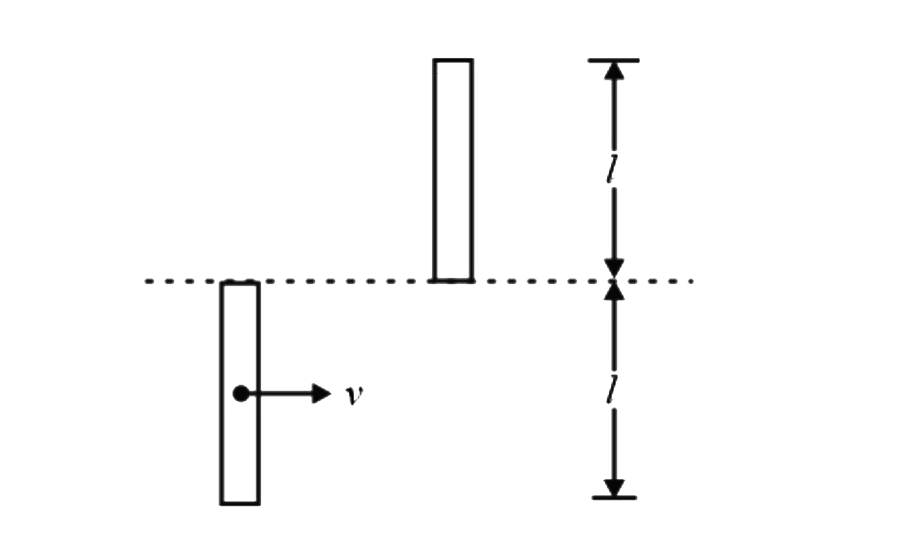
A bar of mass m and length l is in pure translational motion with its centre of mass moving with a velocity v. It collides and sticks to another identical bar at rest as shown in the figure. Assuming that after the collision the system of the two bars becomes one composite bar of length 2l, then the angular velocity of the composite bar will be
 View Solution
View SolutionA wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .A15vlB25vlC35vlDvl
.A15vlB25vlC35vlDvl - Question 2 - Select One
A bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .A15vlB25vlC35vlDvl
.A15vlB25vlC35vlDvl - Question 3 - Select One or More
A thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
Adirectly proportional to its length and inversely proportional to its massBindependent of mass and inversely proportional to the square root of its lengthCdependent only upon the acceleration due to gravity and the length of the barDdirectly proportional to its length and inversely proportional to the acceleration due to gravity
A wodden log mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and strikes with velocity v and sticks to it . Find angular velocity of the system immediately after after the collision about O.
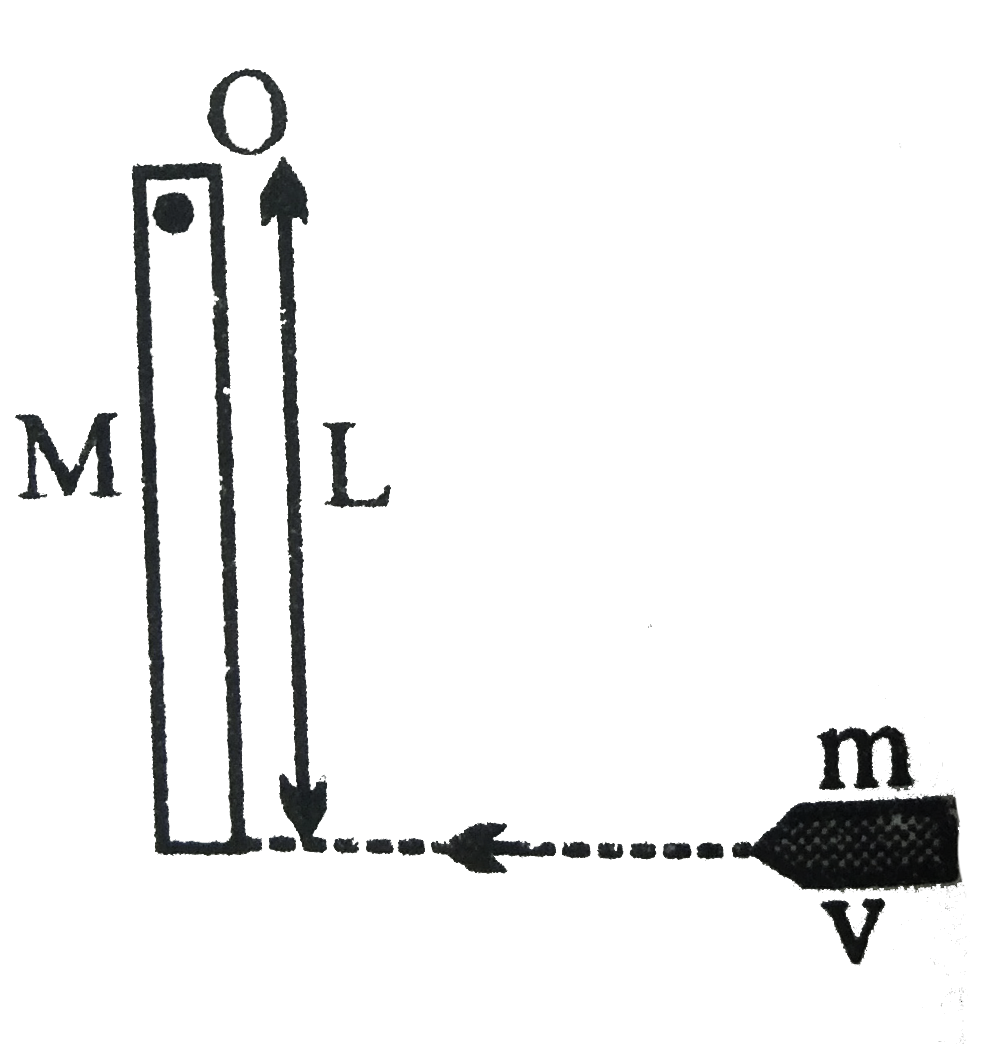 .View Solution
.View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View SolutionA bar of mass m and length l is hanging from point A as shown in the figure . If the Young's modulus of elasticity of the bar is Y and area of cross - section of the wire is A, then the increase in its length due to its own weight will be
 View Solution
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 View Solution
View Solution

