A thin uniform rod $A B$ is sliding between two fixed right angled surfaces. At some instant its angular velocity is $ω$ . If $I_{x}$ represent moment of inertia of the rod about an axis perpendicualr to the plane and passing through the point $X (A, B, C, or D)$ , the kinetic energy of the rod is

A

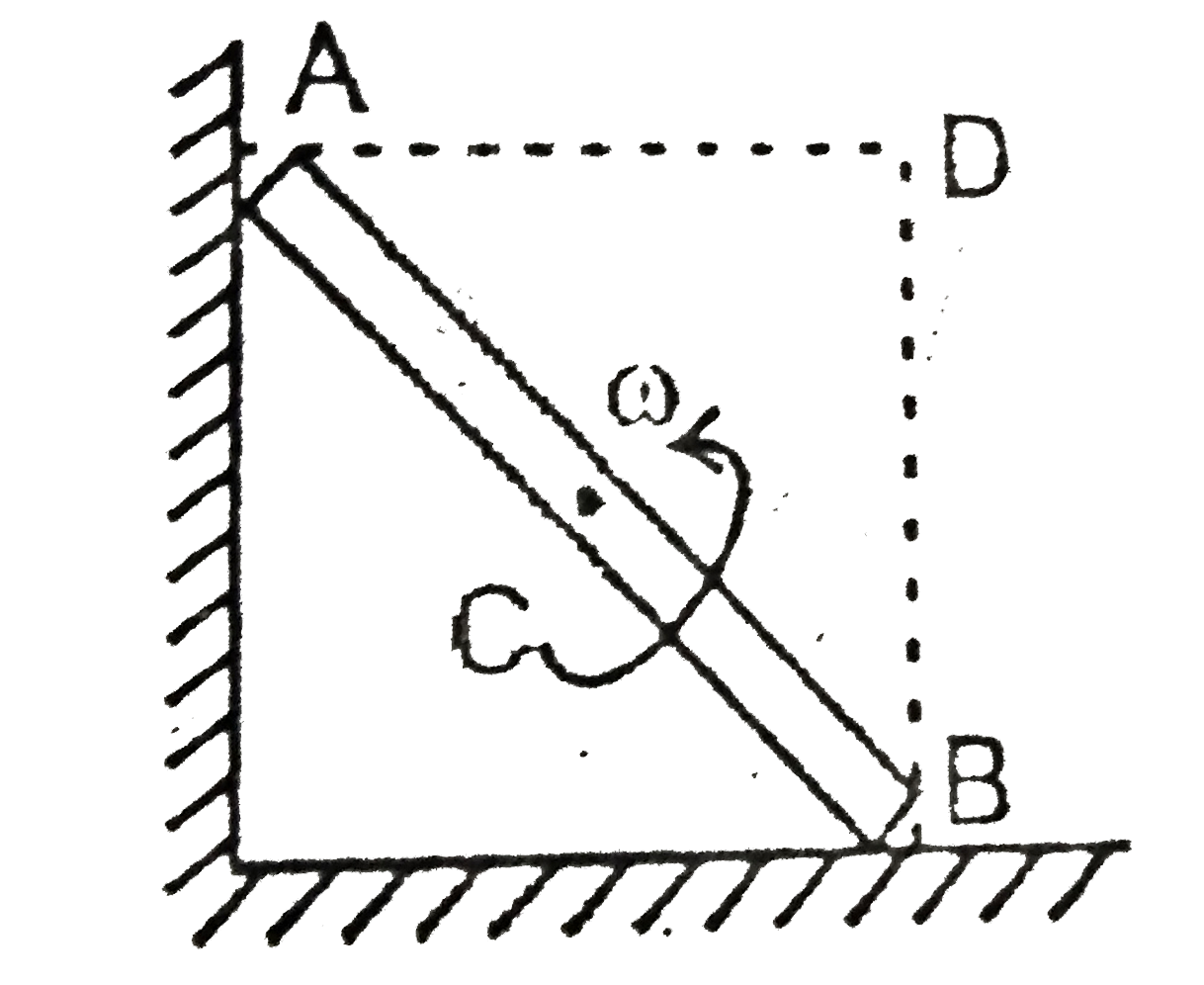
$\frac{1}{2} I_{A} ω^{2}$

B

$\frac{1}{2} I_{B} ω^{2}$

C

$\frac{1}{2} I_{C} ω^{2}$

D

$\frac{1}{2} I_{D} ω^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, D

(Tough) The point $D$ is the instantaneous centre of rotation.
$K . E . = \frac{1}{2} I_{D} ω^{2} = \frac{1}{2} I_{A} ω^{2} = \frac{1}{2} I_{B} ω^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $l_{1}$ is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and $l_{2}$ is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of $I_{1}$ to $I_{2}$ is
A $l : l = 1 : 1$
B $l : l = π : 3$
C $l : l = π : 4$
D $l : l = 3 : 5$
Question 2 - Select One
Moment of inertia of a thin rod of mass 'M' and length 'L' about the axis perpendicular to the rod and passing through its centre is ............
A $M L^{\frac{2}{4}}$
B $M L^{\frac{2}{6}}$
C $M L^{\frac{2}{12}}$
D $M L^{\frac{2}{2}}$
Question 3 - Select One
The moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
A $\frac{I}{4}$
B $\frac{I}{2}$
C $2 I$
D $4 I$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 66

Home
Ask Doubt
Profile