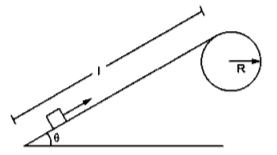
Figure shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. a.Find the minimum projected speed $v_{0}$ for which the particle reaches the top of the track. b. Assuming that the projection speed is $2 v_{0}$ and that the block does not lose contact with the track before reading its top, find the force acting on it when it reaches the top. c. Assuming that the projection speed is only slightly greater than $v_{0}$ where will the block lose contact with the track?

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a) $\sqrt{2 g [R (1 - cos θ) + l sin θ]}$
(b) $6 m g (1 - cos θ + \frac{l}{R} sin θ)$
$(c)$ The radius through the particle makes an angle ${cos}^{- 1} (2 / 3)$ with the vertical

$(a) \frac{1}{2} m v_{0}^{2} = m g l sin θ + m g R (1 - cos θ)$
$v_{0} = \sqrt{2 g R (1 - cos θ) + 2 g l sin θ}$

$(b) C . O . E .$
$= \frac{1}{2} m {(2 v_{0})}_{0}^{2} = m g l sin θ - m g R (1 - cos θ) = \frac{1}{2} m v^{2}$
$= 2 m v_{0}^{2} - m g l sin θ - m g R (1 - cos θ) = \frac{1}{2} m v^{2}$
$= 4 m g R (1 - cos θ) + 4 m g l sin θ - m e l sin θ - m g R (1 - cos θ) = \frac{1}{2} m v^{2}$
$= 6 m g R (1 - cos θ) + 6 m g l sin θ = m v^{2}$
$N = 6 m g (1 - cos θ) + 6 m g$ $\frac{l}{R} sin θ$
$= 6 m g [(1 - cos θ) + \frac{l}{R} sin θ]$

$m g cos θ = \frac{m v^{2}}{R}$
$= \frac{1}{2} m v^{2} = \frac{1}{2} m g R cos θ$
$= m g R (1 - cos θ) = \frac{1}{2} m g R cos θ$
$cos θ = \frac{2}{3} t e h t a = {cos}^{- 1} (\frac{2}{3})$ .

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 69

Home
Ask Doubt
Profile