In the figure shown the acceleration of A is, then the acceleration of B is (A remains in contact in B)

The correct Answer is:D

From wedge constant
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.399videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4020videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.379videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
In fig, the acceleration of A is →aA=15ˆi+15ˆj. Then the acceleration of B is (A remains in constact with B)
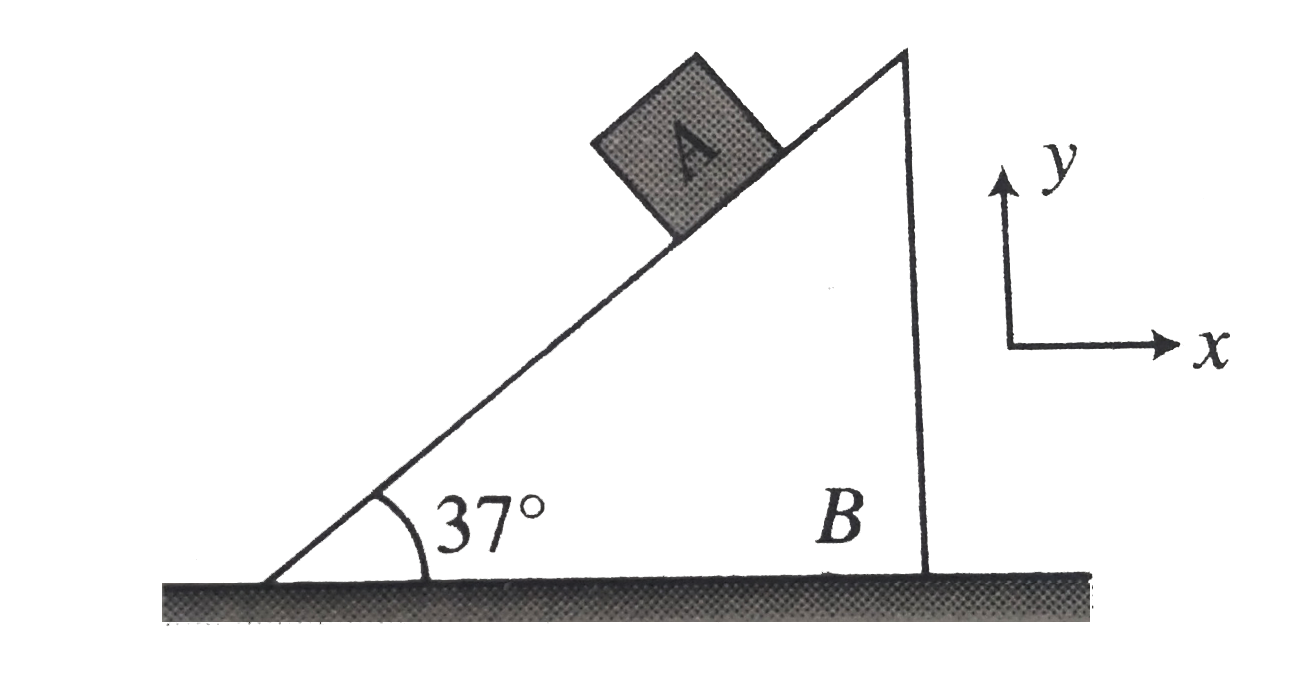 A6ˆiB−15ˆiC−10ˆiD−5ˆi
A6ˆiB−15ˆiC−10ˆiD−5ˆi - Question 2 - Select One
In the figure shown the accelerationof A is aA=(15ˆi+15ˆj). Then the acceleration of B is (A remain in contact with B)
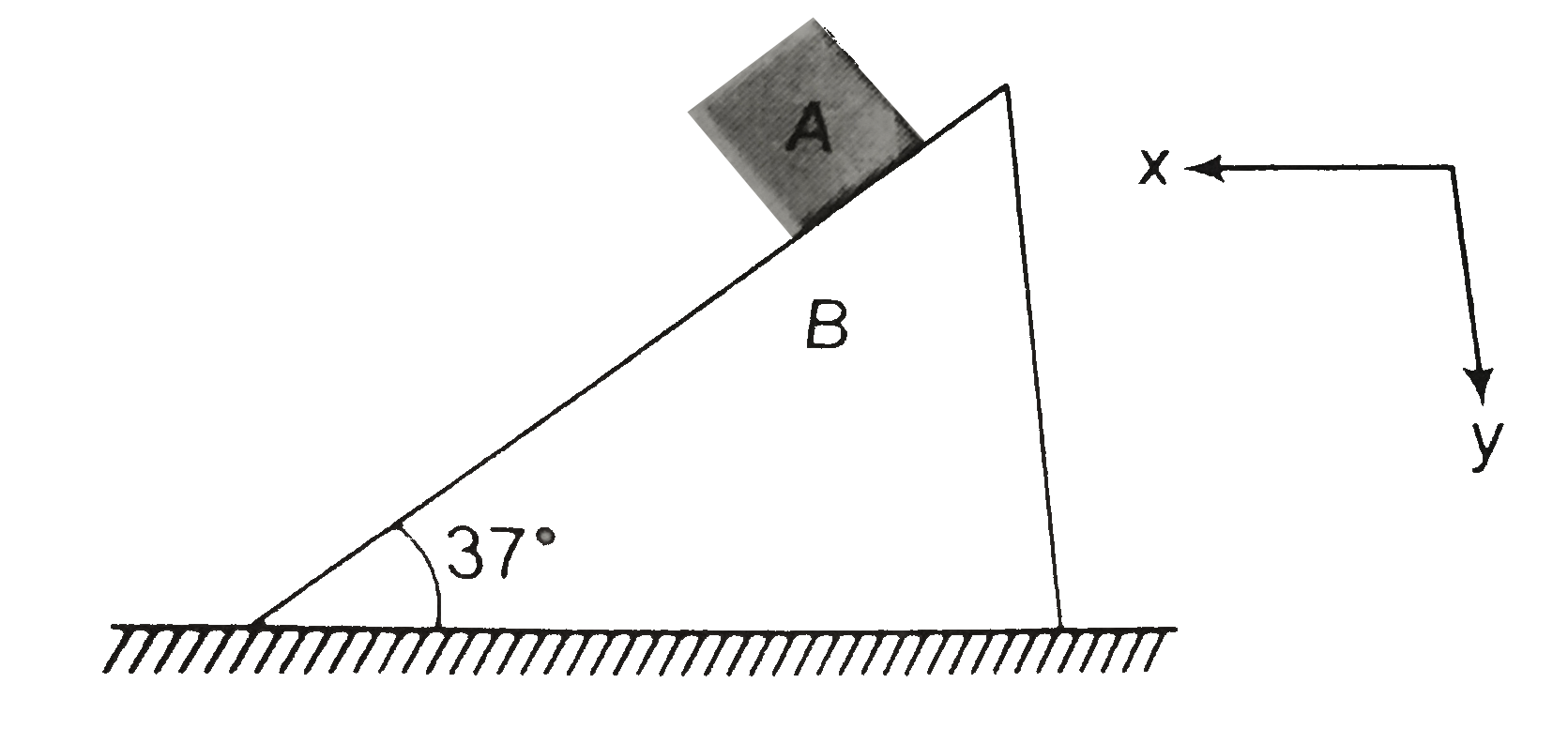 A5ˆiB−15ˆiC−10ˆiD−5ˆi
A5ˆiB−15ˆiC−10ˆiD−5ˆi - Question 3 - Select One
The velocities of two particles AandB of same mass are →VA=aˆi and →VB=bˆj where a and b are constants. The acceleration of particle A is (2aˆi+4bˆj) and acceleration of particle B is (aˆi−4bˆj) in (m/s2). The centre of mass of two particle will move in :
Astraight lineBparabolaCellipseDcircle
A charged particle has acceleration →a=2ˆi+xˆj in a megnetic field →B=−3ˆi+2ˆj−4ˆk. Find the value of x.
View SolutionA point charge +q0 is projected in a magnetic field →B=(ˆi+2ˆj−3ˆk). If acceleration of the particle is →a=(2ˆi+bˆj−ˆk) then value of b will be
View SolutionA block Ais just placed inside a smooth box B as shown in figure. Now the box is given an acceleration a=(2ˆi−2ˆj)m/s−2. Under the acceleration block A cannot remain in the position shown.
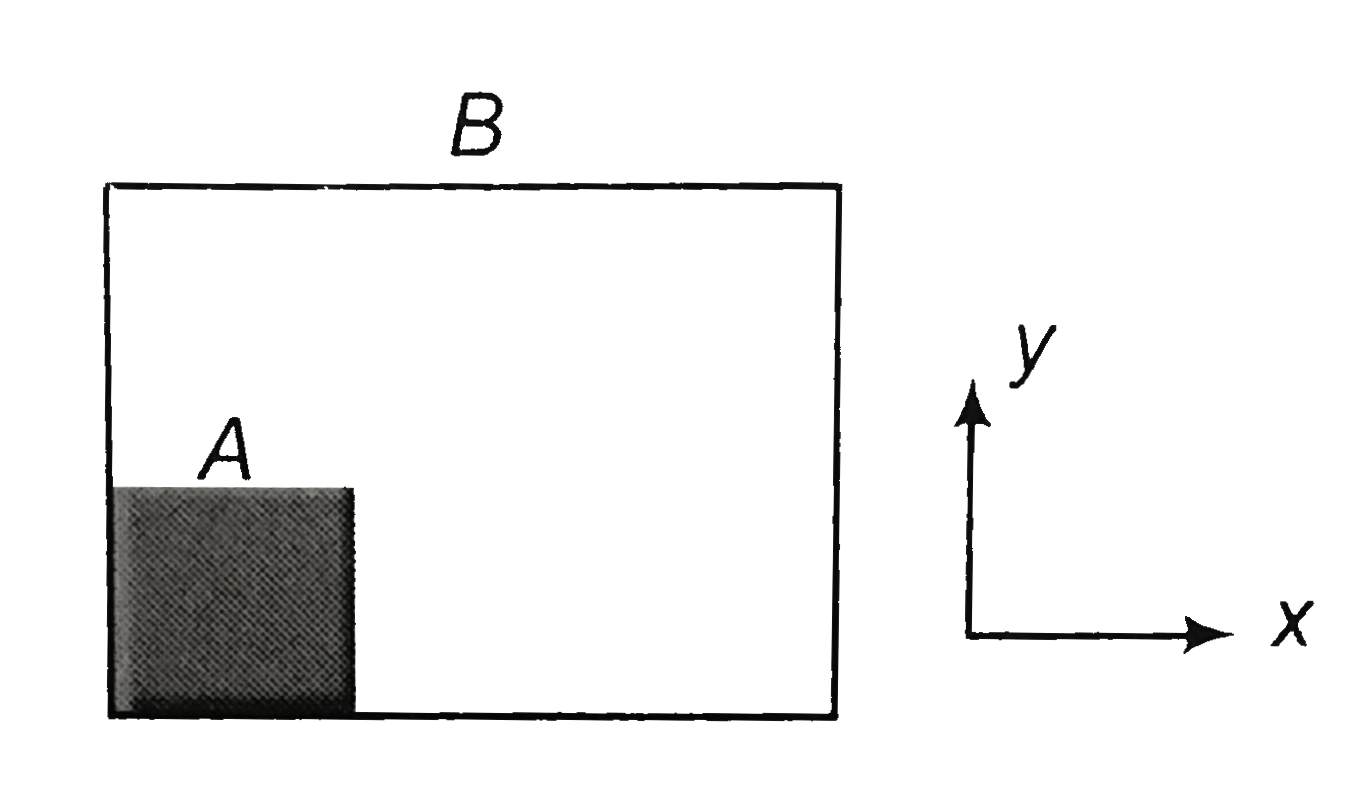
Block will require ma force for moving with acceleration a.View SolutionIn the figure shown the velocity of A with respect to ground is (20ˆi+15ˆj)m/s, then what will be the magnitude of velocity of the wedge 'B' with respect to ground frame. (A remains in contact with B)
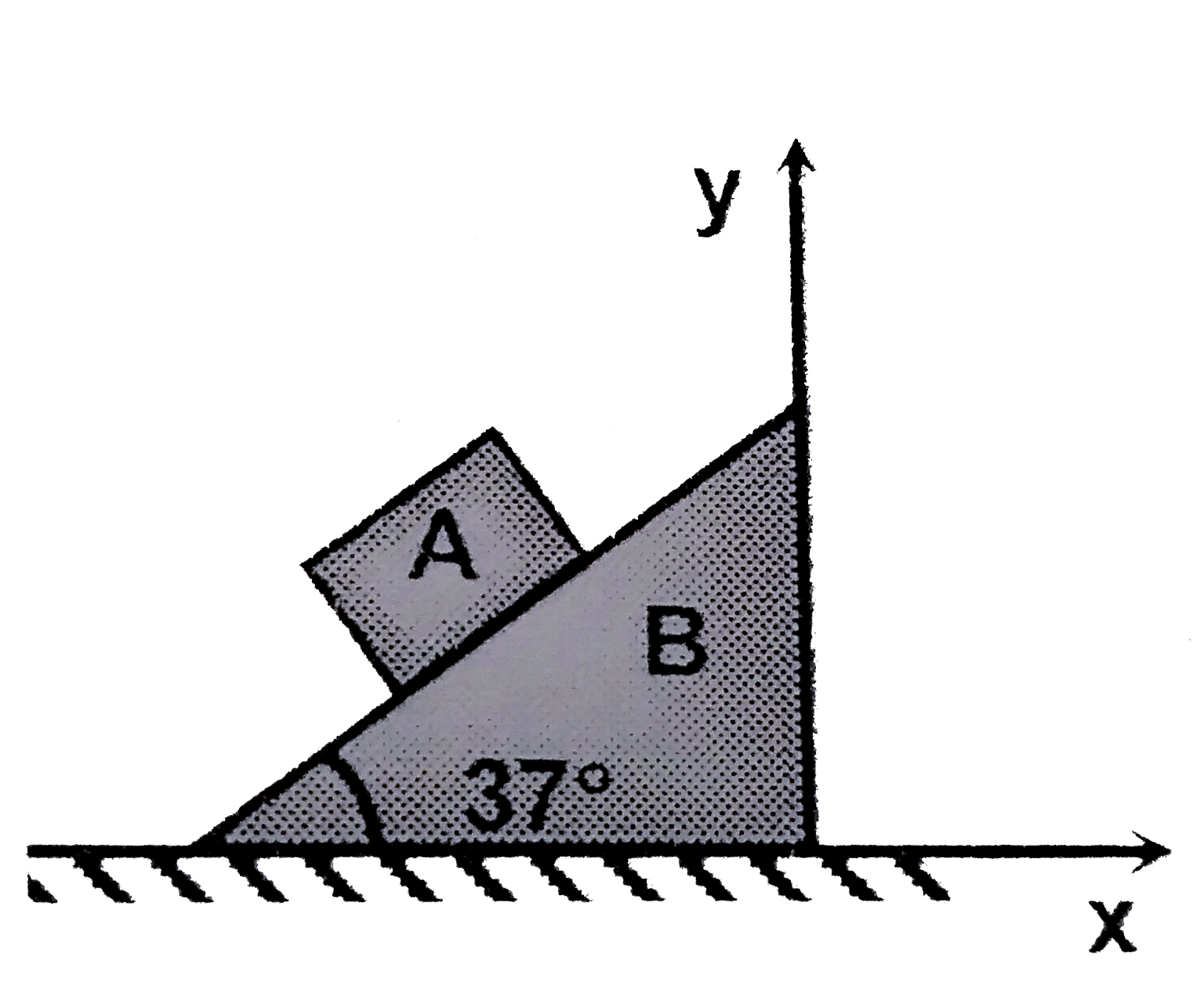 View Solution
View SolutionIf →A=3ˆi−4ˆj and →B=2ˆi+16ˆj then the magnitude and direction of →A+→B will be
View Solution

