In a arrangement, 3n cells of emf ε and internal resistance r are connected in series. Out of 3n cells polarity of n cells is reversed. Current in the circuit is
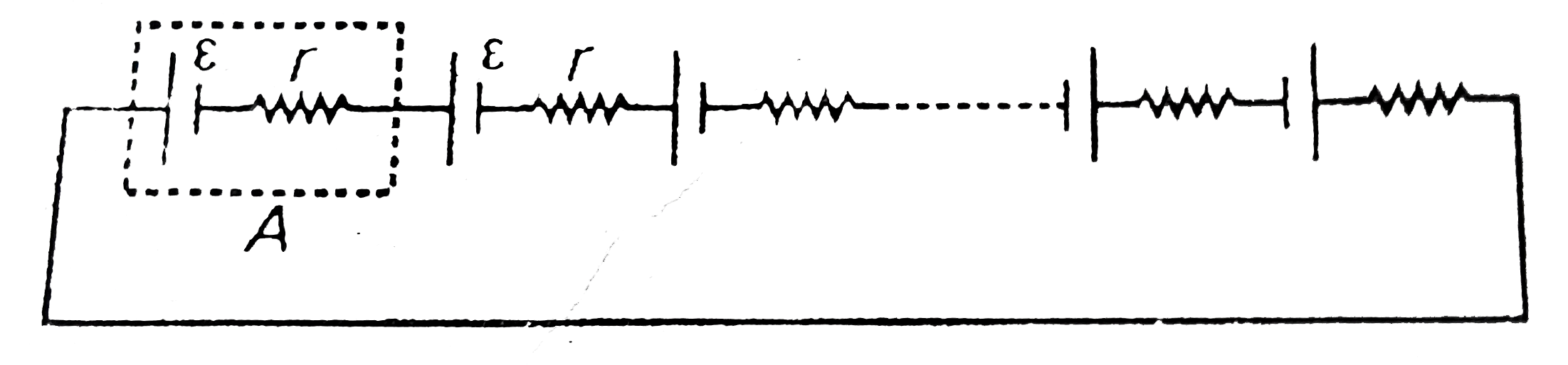
2εlor
2ε3r
ε3r
εr
The correct Answer is:C
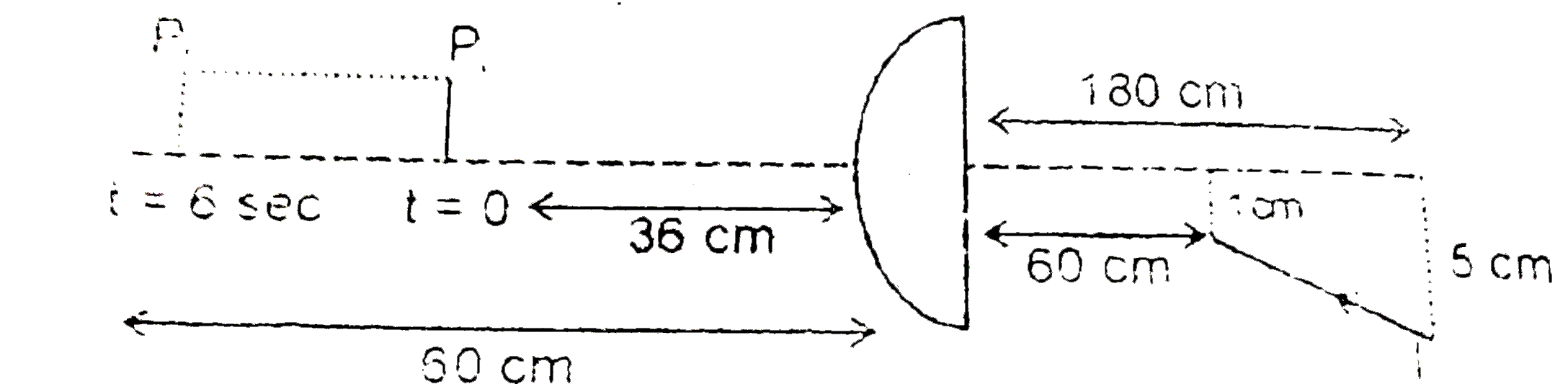
1f=(32−1)(115)
f=30 cm
1v+136=130⇒1v=130−136=1180
v=180 cm.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.399videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4020videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.379videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
n-identical cells each of emf E and internal resistance r are connected in series. Find the expression for current in the circuit given below
 View Solution
View SolutionTen cells each of emf 1V and internal resistance 1Ω are connected inseries. In this arrangement, polarity of two cells is reversed and the system is connected to an external resistance of 2Ω. Find the current in the circuit.
View Solution
Knowledge Check
- Question 1 - Select One
Four cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
A2E4r+RB3E4r+RC3E3r+RD2E3r+R - Question 2 - Select One
A cell of emf ε and internal resistance r is charged by a current I, then
Athe cell stores chemical energy at the rate of εiBthe cell stores chemical energy at the rate of i2rCthe cell stores chemical energy at the rate of εI−i2rDthe storage of chemical energy rate cannot be calculated - Question 3 - Select One
Twenty cells each of emf E and internal resistance r are connected in series to form a loop . If polarity of one of the cell is reserved, then terminal potential across this cell is
A19E10B11E10C9E10DZero
Four identical cells of emf ε and internal resistance r are to be connected in series. Suppose, if one of the cell is connected wrongly, then the equivalent emf and effective internal resistance of the combination is
View SolutionN identical cells, each of emf ε and internal resistances r are joined in series. Out of these, n cells are wrongly connected, i.e. their terminals are connected in reverse order as required for series connection. If εo be the emf of the resulting battery and ro be its internal resistance then for n <N/2
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to from a closed circuit. One cell A is joined with reversed polarity. The potential difference across each cell, except A, is
View Solutionn identical cells, each of emf ε and internal resistance r, are joined in series to form a closed circuit. One cell A is joined with reversed polarity. The potential difference across any one cell is
View SolutionIf n cells each of emf E and internal resistance are connected in parallel, then the total emf and internal resistances will be
View Solution

