Two equal masses are connected by a spring satisfying Hook's law and are placed on a frictionless table. The spring is elongated a little and allowed to go. Let the angular frequency of oscillations be $ω$ . Noe one of the masses is stopped. The square of the new angular frequency is $:$

A

$ω^{2}$

B

$\frac{ω^{2}}{2}$

C

$\frac{ω^{2}}{3}$

D

$2 ω^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

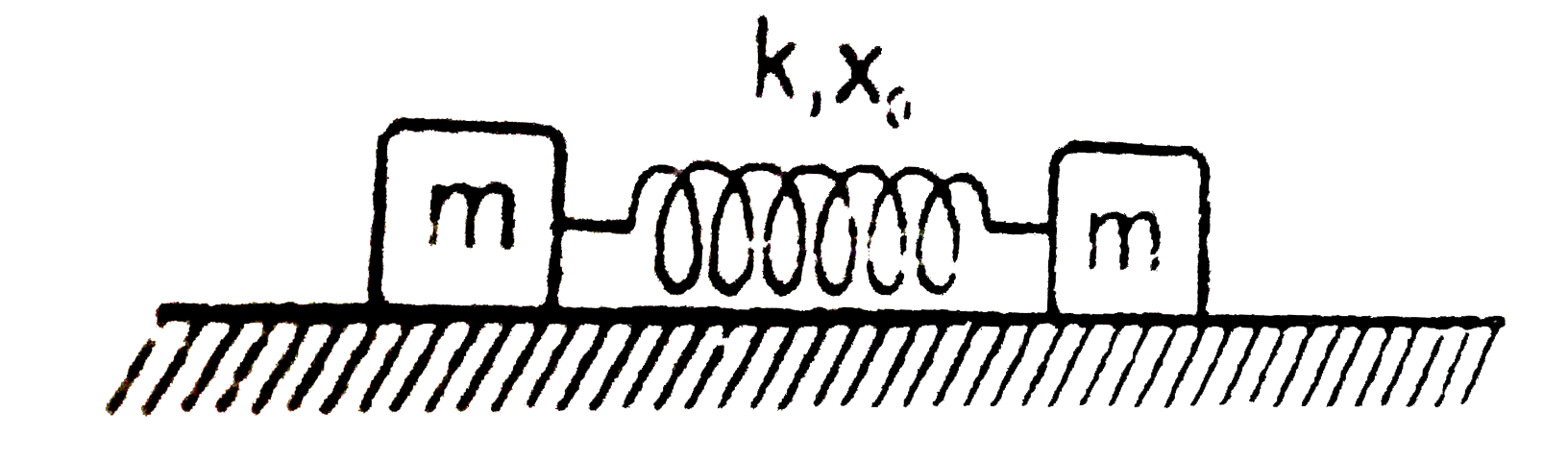
$\sqrt{\frac{k}{μ}} = ω \Rightarrow μ = \frac{m_{1} m_{2}}{m_{1} + m_{2}}$
$ω = \sqrt{\frac{2 k}{m}} \Rightarrow ω_{2} \sqrt{\frac{k}{m}}$
$ω_{2}^{2} = \frac{k}{m} = \frac{ω^{2}}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two masses $m_{1}$ and $m_{2}$ connected by a spring of spring constant k rest on a frictionless surface. If the masses are pulled apart and let go, the time period of oscillation is-
A $T = 2 π \sqrt{\frac{1}{k} (\frac{m_{1} m_{2}}{m_{1} + m_{2}})}$
B $T = 2 π \sqrt{\frac{1}{k} (\frac{m_{1} + m_{2}}{m_{1} m_{2}})}$
C $T = 2 π \sqrt{(\frac{m_{1}}{k})}$
D $T = 2 π \sqrt{(\frac{m_{2}}{k})}$
Question 2 - Select One
Two spring are connected toa block of mass $M$ placed a frictionless surface as shown if both the spring have a spring constant $k$ the frequency of oscillation block is

A $\frac{1}{2 π} \sqrt{\frac{k}{2 M}}$
B $\frac{1}{2 π} \sqrt{\frac{k}{M}}$
C $\frac{1}{2 π} \sqrt{\frac{2 k}{M}}$
D $\frac{1}{2 π} \sqrt{\frac{M}{k}}$
Question 3 - Select One
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
A $\frac{1}{2 π} \sqrt{\frac{m}{k}}$
B $\frac{1}{2 π} \sqrt{2 \frac{k}{m}}$
C $\frac{1}{2 π} \sqrt{3 \frac{k}{m}}$
D $\frac{1}{2 π} \sqrt{\frac{m}{k}}$

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.38

Home
Ask Doubt
Profile