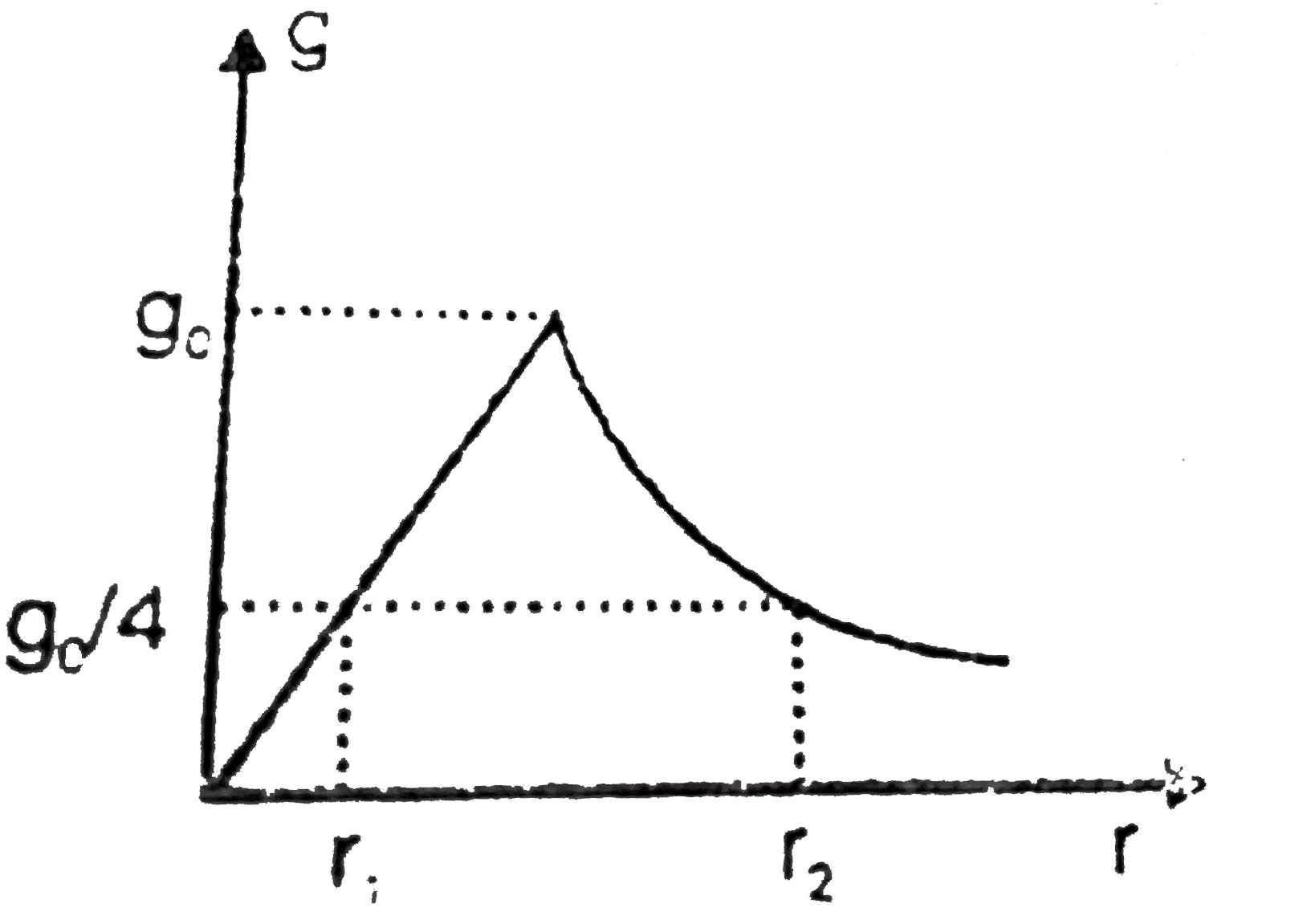
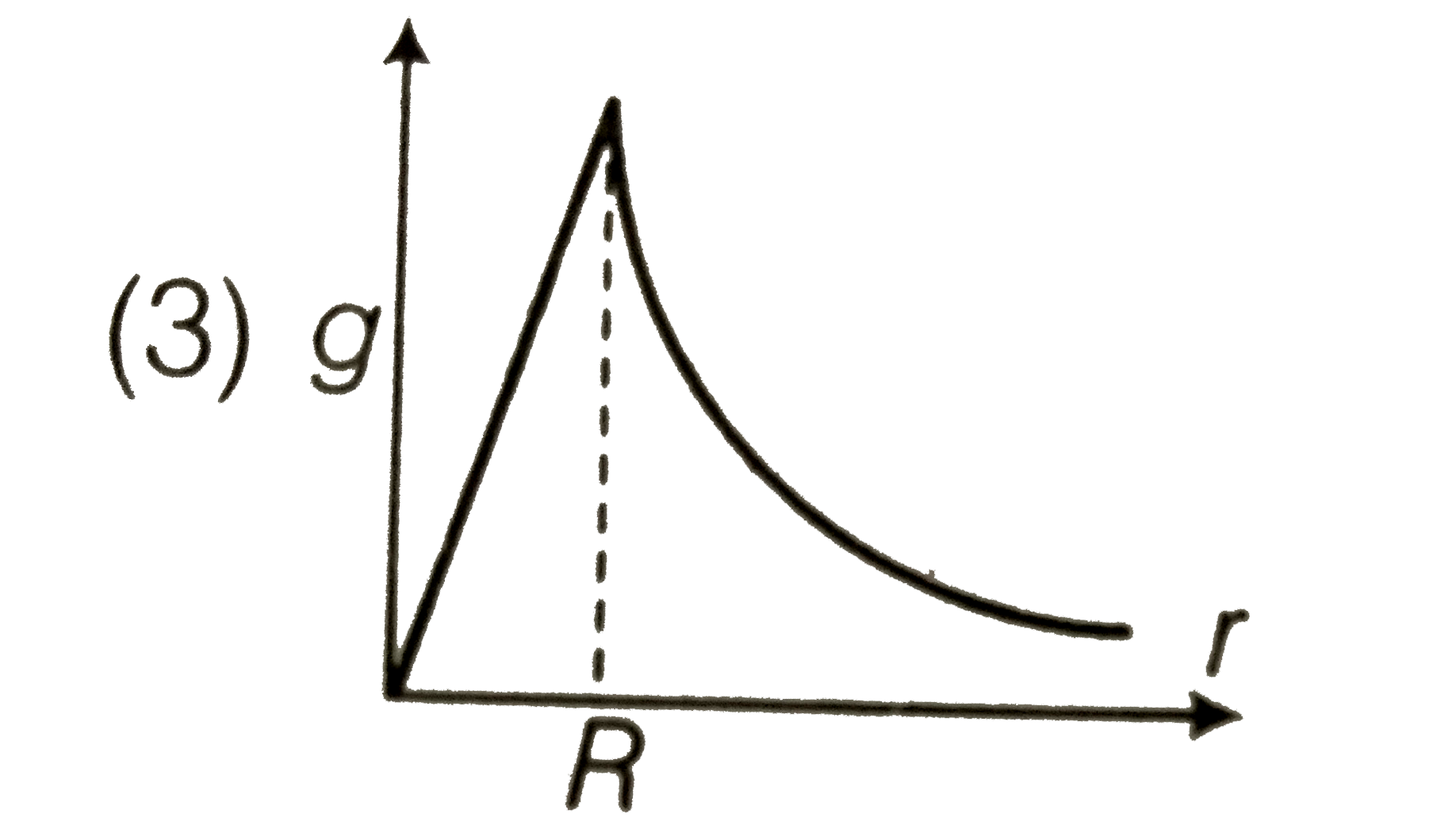
Figure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
R4
7R4
4R3
2R
The correct Answer is:B
Inside planet
904g0(1−dR)⇒d=3R4
Outside planet
g=g0(R2)(r+h)2⇒h=R .
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.419videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4220videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.399videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
The ratio of acceleration due to gravity at depth 'R' from the surface of planet and at height ' r' from the surface of planet where r
View SolutionThe dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
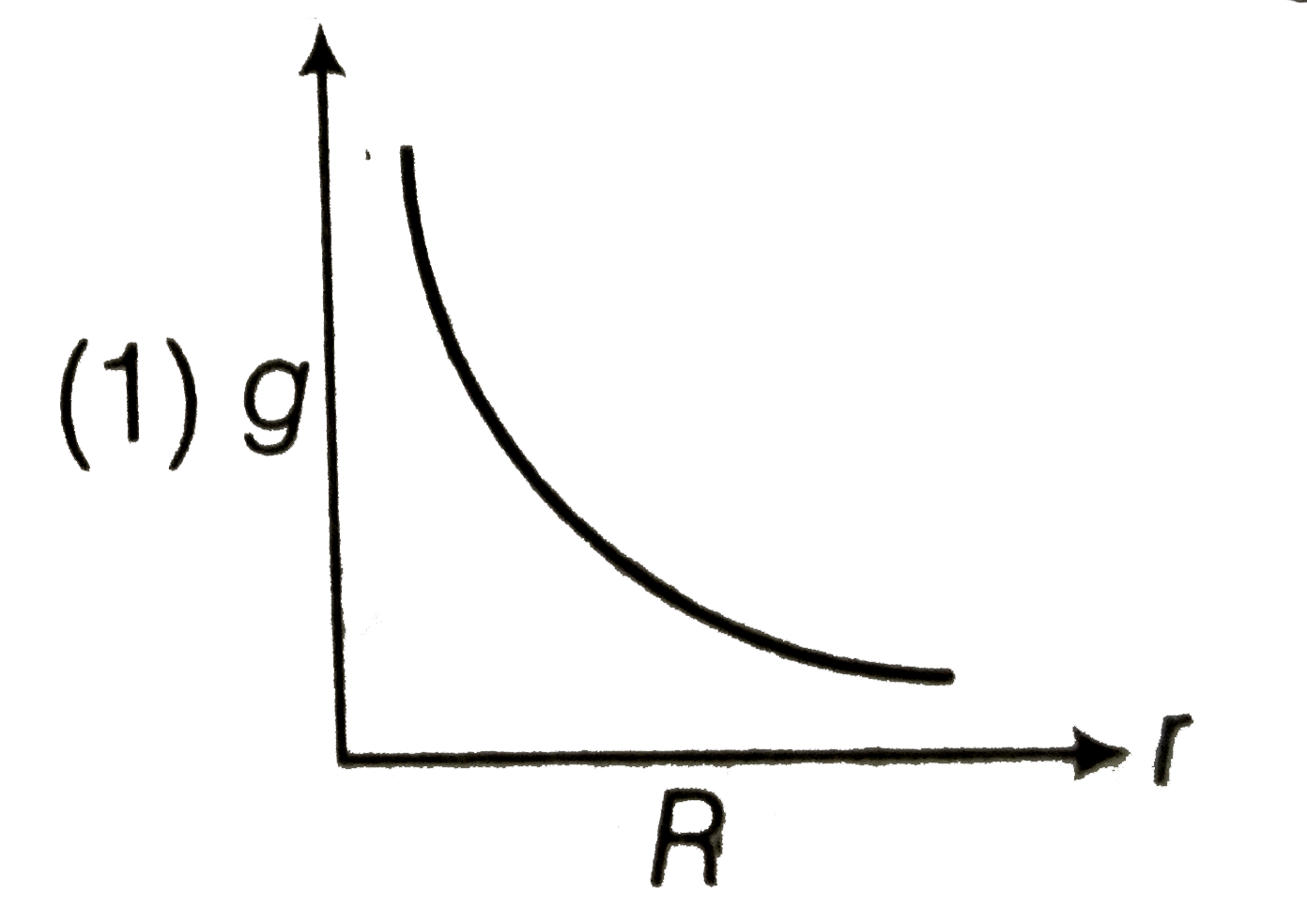
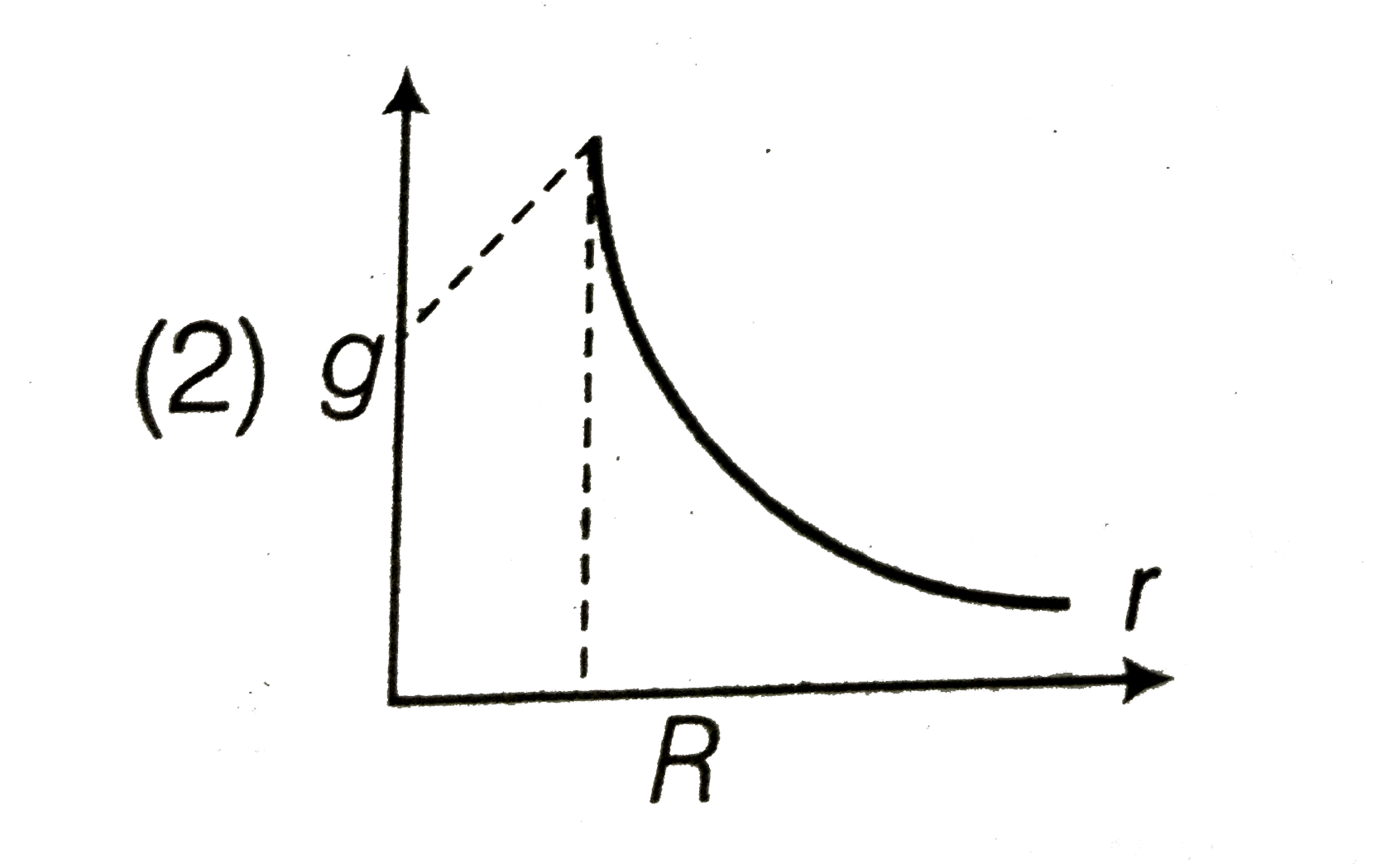
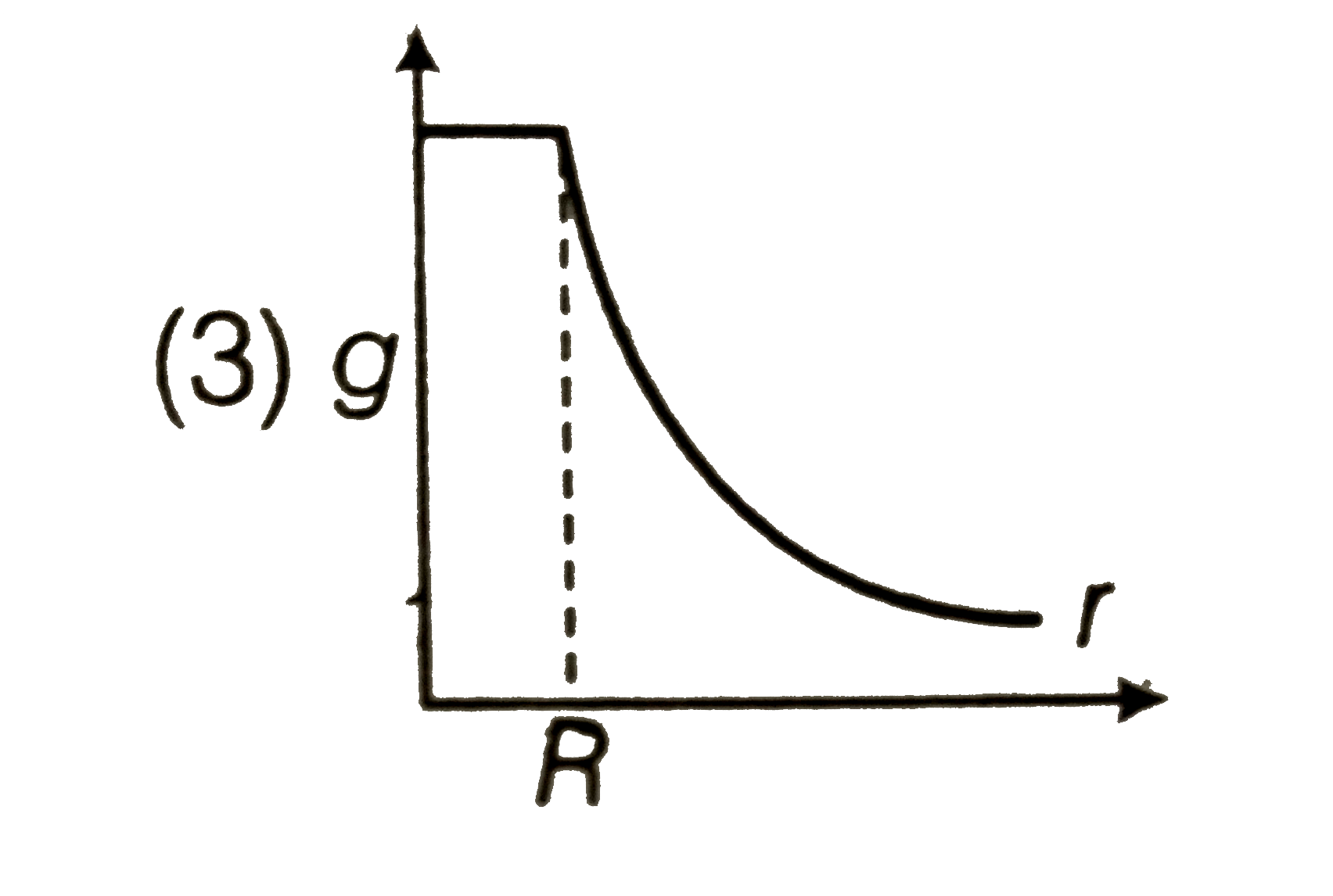
The correct figure isView Solution
Knowledge Check
- Question 1 - Select One
Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
A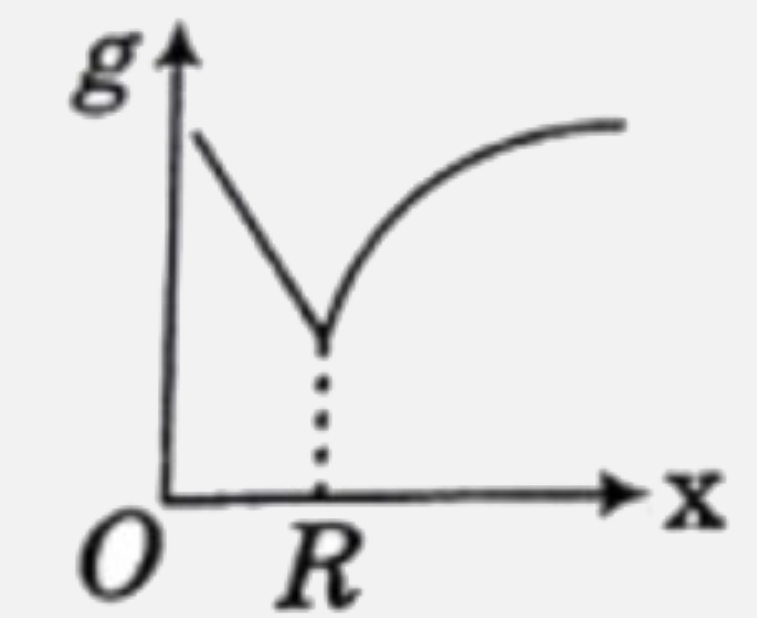 B
B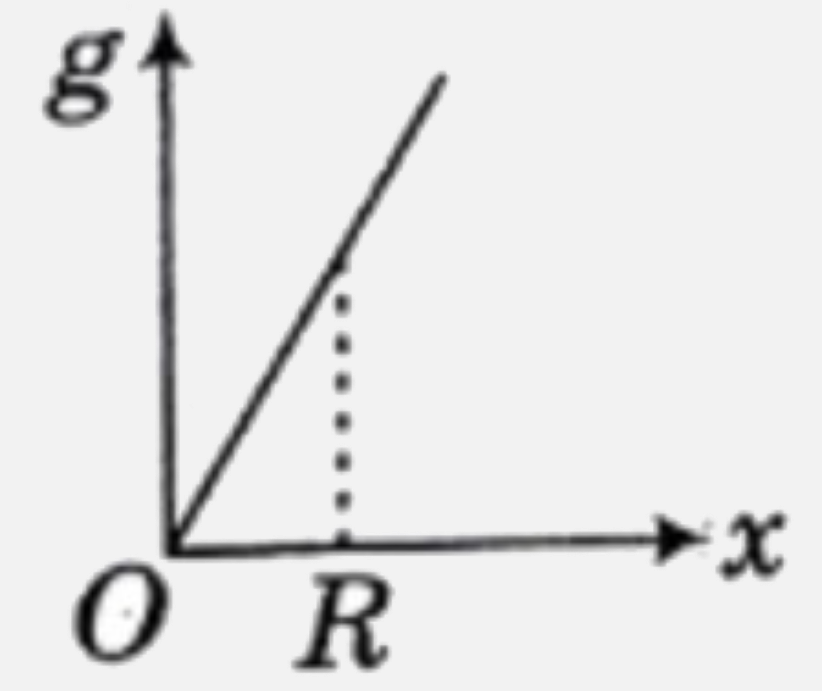 C
C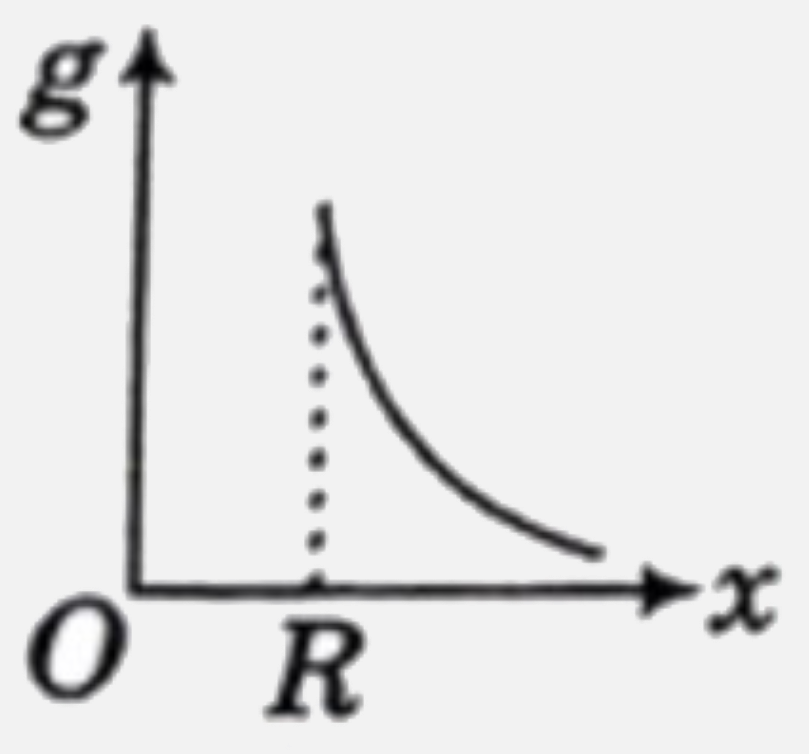 D
D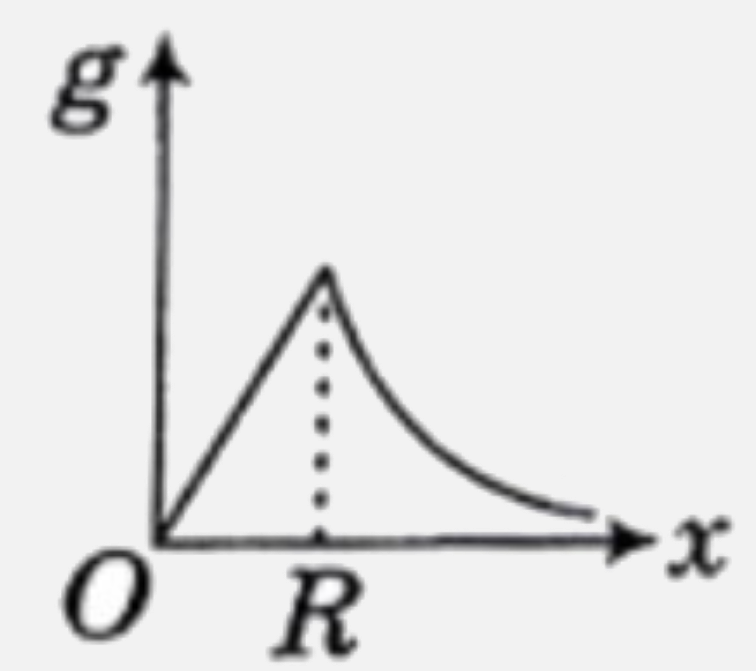
- Question 2 - Select One
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
Ag∝rBg∝r2Cg∝r−1Dg∝r−2 - Question 3 - Select One
The acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
AρRBρR−1Cρ−1R−2DρR2
If g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
View SolutionA particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View SolutionThe acceleration due to gravity near the surface of a planet of radius R and density d is proportional to
View Solution

