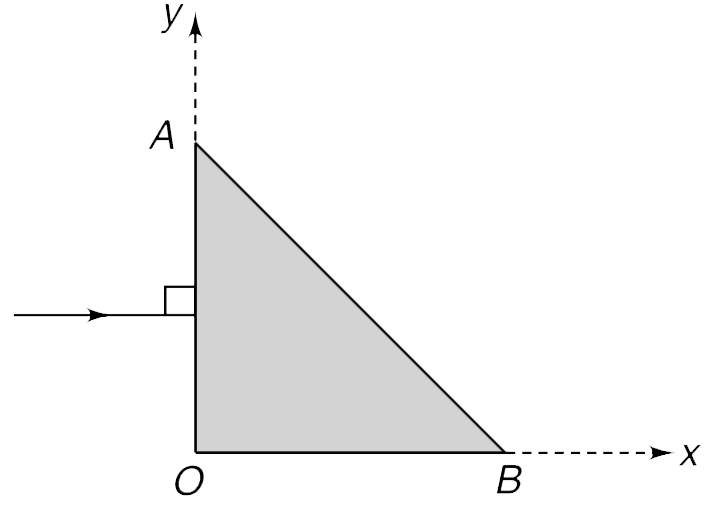
A triangular medium has varying refracting index μ=μ0+ax where x is the distance (in cm) along x-axis from origin and m0=4/3. A ray is incident normally on face OA at the mid-point of OA. Find the range of value of a so that light does not escape through face AB when it falls first time on the face AB.
a>19
a>29
a>13
None of these
The correct Answer is:B

Clearly PM=32cm
37∘>sin−11n0+a(3/2)
35>1n1+3a2⇒3n0+9a2>5
9a2>1⇒a>29.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4320videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4410videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.419videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
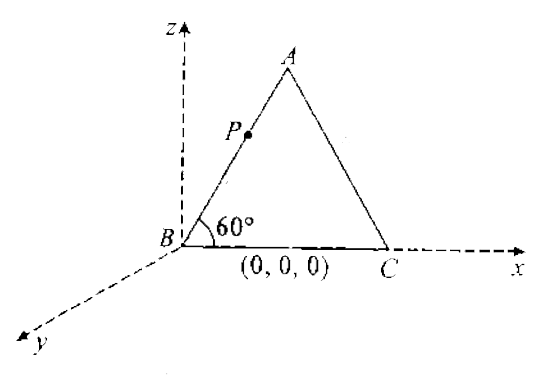
An equilateral prism ABC is placed in air with its base side BC lying horizontally along x-axis as shown in the figure. A ray given by √3z+x=10 is incident at a point P on the face AB of the prism
(a) Find the value μ from which the ray grazes the face AB
(b) Find the direction of the initially refracted ray if μ=32
(c) Find the equation of ray coming out of the prism if bottom BC is silvered ?
 View Solution
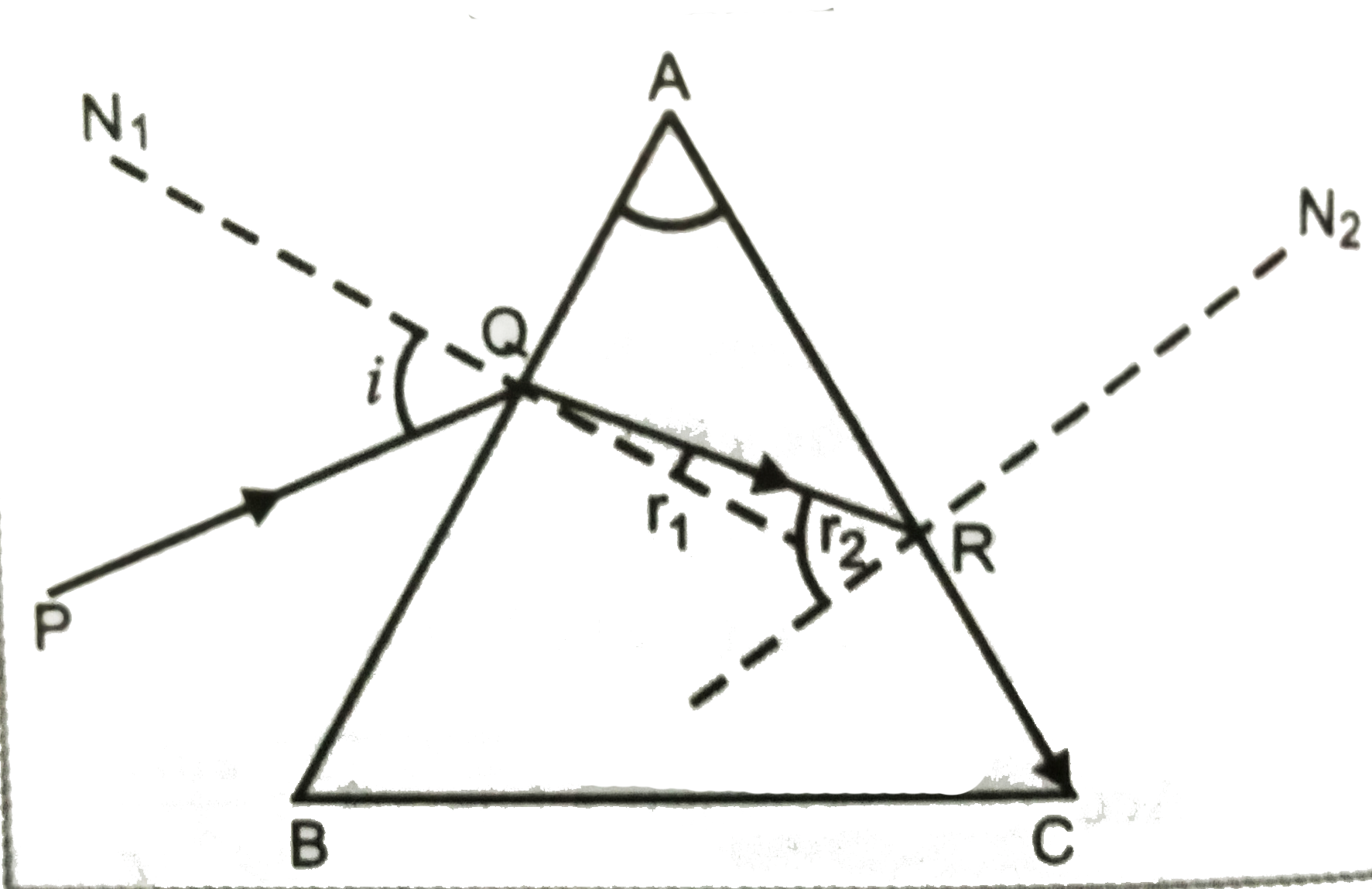
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View Solution
Knowledge Check
- Question 1 - Select One
A triangular medium has varying refracting index n=n0+ax, where x is the distance (in cm) along x-axis from origin and n0=43. A ray is incident normally on face OA at the mid-point of OA. The range of a so that light does not escape through face AB when it falls first time on the face AB(OA=4cm, OB=3cm and AB=5cm): (Surrounding medium is air)
 Aa>19Ba>29Ca>13Dnone of these
Aa>19Ba>29Ca>13Dnone of these - Question 2 - Select One
In figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit S1 passes through a medium of variable refractive index μ=1+ax (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on S1. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength λ in air) is
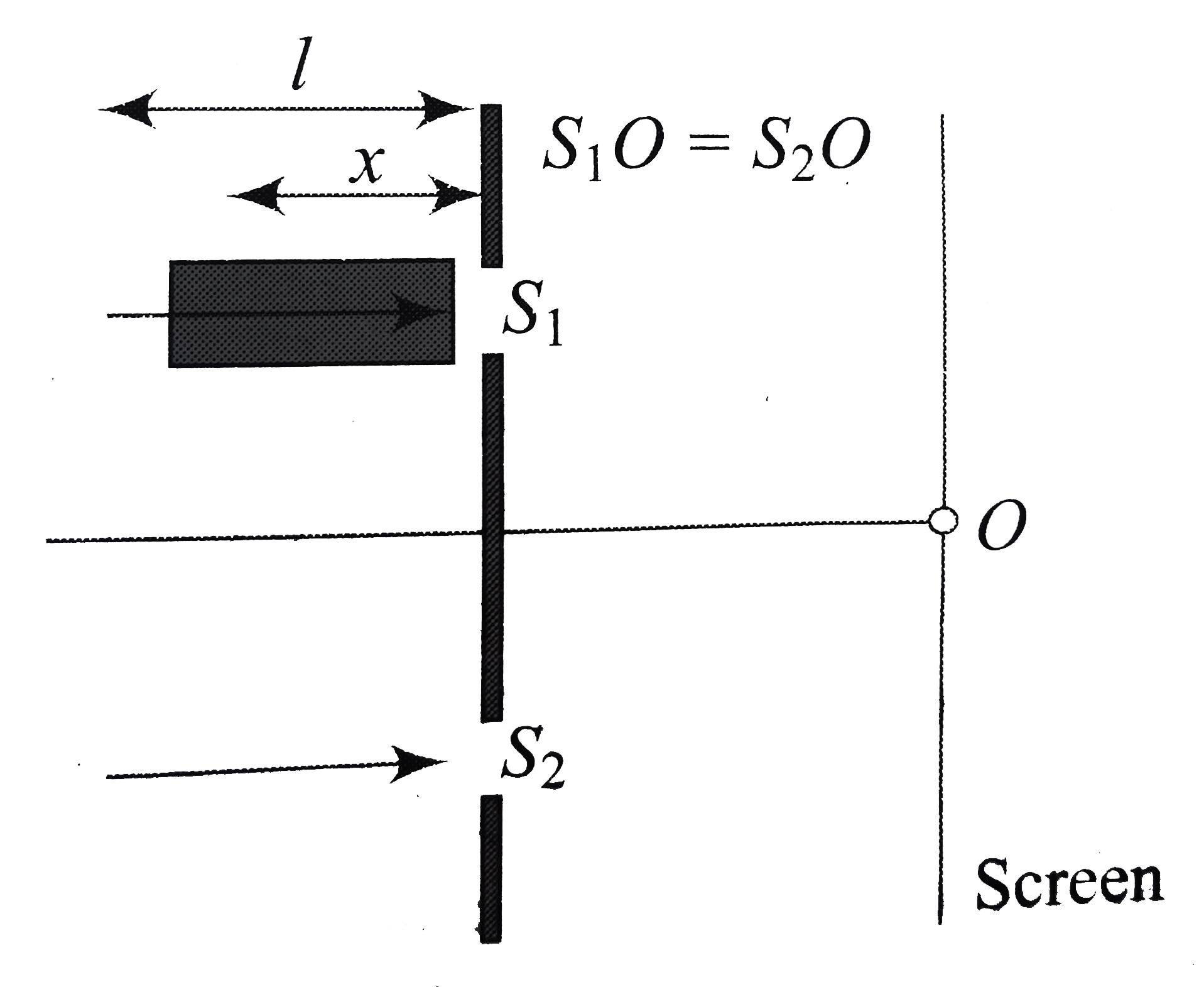 AλlBλl2Cl2λDnone of these
AλlBλl2Cl2λDnone of these
A ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
 View Solution
View SolutionCalculate the value of θ, for which light incident normally on face AB grazes along the face BC.
μglass=3/2andμwater=4/3
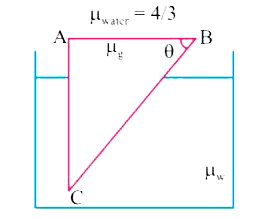 View Solution
View SolutionThe refractive index of a medium changes asμ=μ0[1−x2+y2d2]1/2where μ0 is the refractive index on the z axis. A plane wavefront (AB) is incident along z axis as shown in the figure. Draw the wavefront at a later timeΔt. Is the wavefront getting focused?
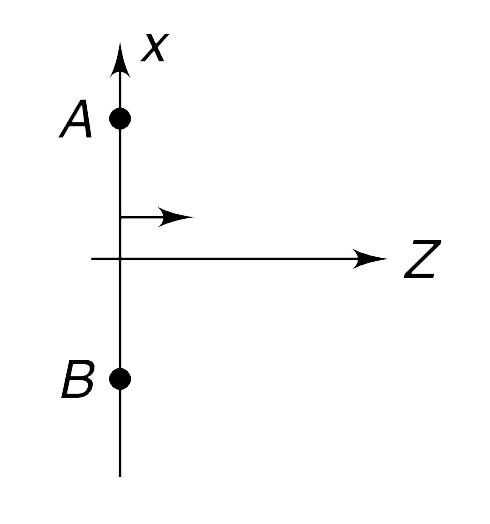 View Solution
View SolutionA parallel beam of light travelling in x direction is incident on a glass slab of thickness t. The refractive index of the slab changes with y as μ=μ0(1–y2y02)where μ0 is the refractive index along x axis and y0 is a constant. The light beam gets focused at a point F on the x axis. By using the concept of optical path length calculate the focal length f. Assumef>>t and consider y to be small.
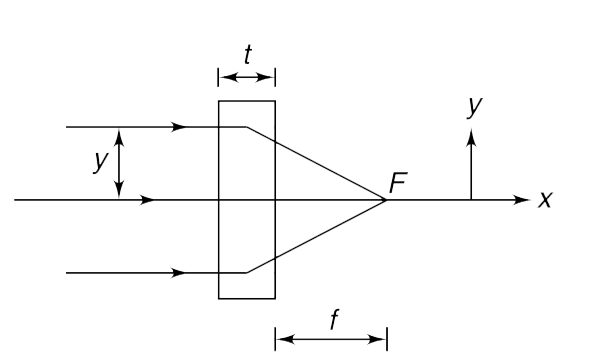 View Solution
View SolutionTwo plane mirrors M1 and M2, placed at right angles, form two sides of a container. Mirror M1 is inclined at an angle θ0 to the horizontal. A light ray AB is incident normally onM1. Now the container is filled with a liquid of refractive index μ so that the ray is first refracted, then reflected at M1. The ray is next reflected at M2 and then comes out of the liquid surface making an angle θ with the normal to the liquid surface. Find θ.
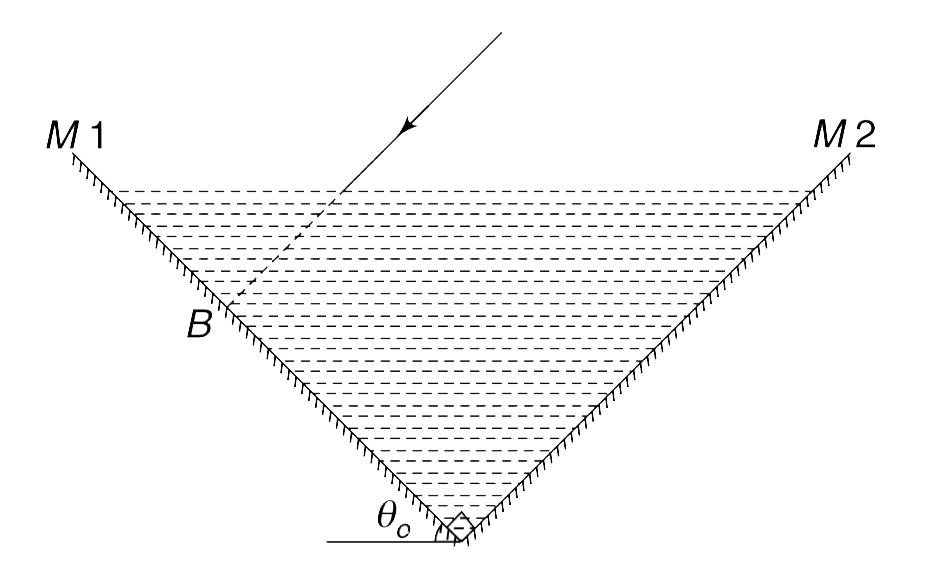 View Solution
View SolutionTwo identical equilat- eral glass (refractive index =√2) prisms ABC and CDE are kept such that the angle between faces AC and CE is q. A ray of light is incident at an angle i at the face AB and traverses through the two prisms along the path PQRSTU. Find the value of angle i and θ such that angle between the incident ray PQ and emergent ray TU is minimum.
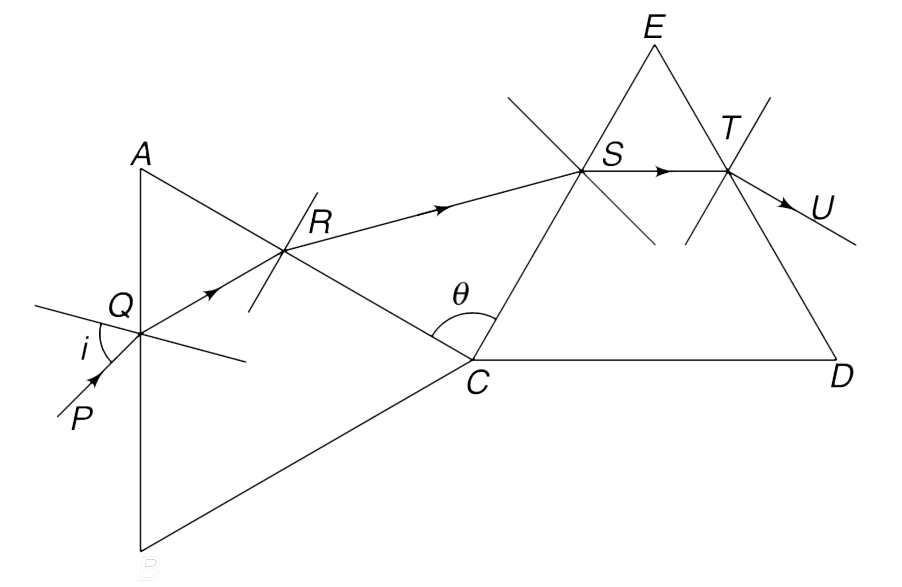 View Solution
View Solution

