A particle of charge q0 and of mass m0 is projected along the y-axis at t=0 from origin with a velocity V0. If a uniform electric field E0 also exist along the x-axis, then the time at which debroglie wavelength of the particle becomes half of the initial value is:
m0v0q0E0
2m0v0q0E0
√3m0v0q0E0
3m0v0q0E0
The correct Answer is:C
Initial debrogle wavelength =hm0v0
After any time t=λ=hm0v0+q0E0t
When λ becomes half of the initial value :
h2m0v0=hm0v0+q0E0t
⇒m0v0=q0E0t⇒t=√3m0v0q0E0.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.43
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.44
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.41
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A particle of specific charge α is projected from origin with velocity v=v0ˆi−v0ˆk in a uniform magnetic field B=−B0ˆk. Find time dependence of velocity and position of the particle.
View SolutionA particle of charge q and mass m released from origin with velocity →v=v0ˆi into a region of uniform electric and magnetic fields parallel to y-axis. i.e., →E=E0ˆjand→B=B0ˆj. Find out the position of the particle as a functions of time
Strategy : Here →E∣∣→B
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
ay=Fym=Fem=qE0m
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
→v(t)=vxˆi+vyˆj+vzˆk
View Solution
Knowledge Check
A positively charge particle moving along x-axis with a certain velocity enters a uniform electric field directed along positively y-axis. Its
AVertical velocity changes but horizontal velocity remains constantBHorizontal velocity changes but vertical velocity remiand constantCBoth vertical and horizontal velocities changeDNeither vertical nor horizontal velocity changes.A particle of charge q and mass m enters a region of a transverse electric field of E0ˆj with initial velocity v0ˆi . The time taken for the change in the de Broglie wavelength of the charge from the initial value of λ0 to λ0/3 is proportional to
AqmBmqC√qmD√mqA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
A(0,0,0)B(−mv√2qB,mv√2qB,0)C(−√2mvqB,√2mvqB,0)Dnone of the above
A particle of charge q and mass m is subjected to an electric field E=E0(1−ax2) in the x - direction, where a and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
View SolutionA particle of charge q and mass m starts moving from the origin with a velocity →v.eqv0ˆj under the action of an electric field →E=E5¯i and magnetic field →B=B0→i The speed of the particle will become 2v0 aftet a time t=√xmw0qE0. Find the value of x.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA unifrom electric field having a magnitude E0 and direction along the positive X-axis exists. If the protential V is zero at x=0, then its value at X=+x will be
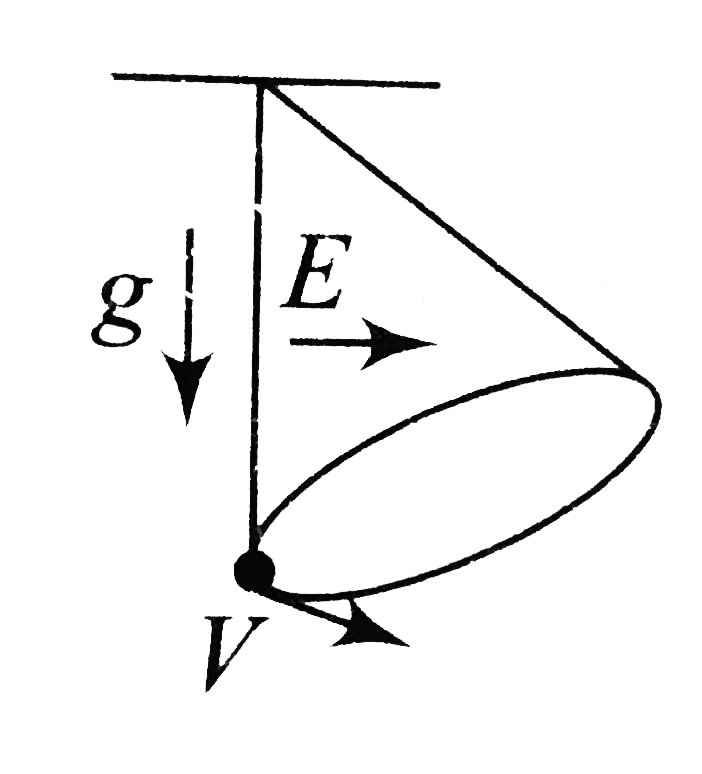
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.
View Solution
