Question

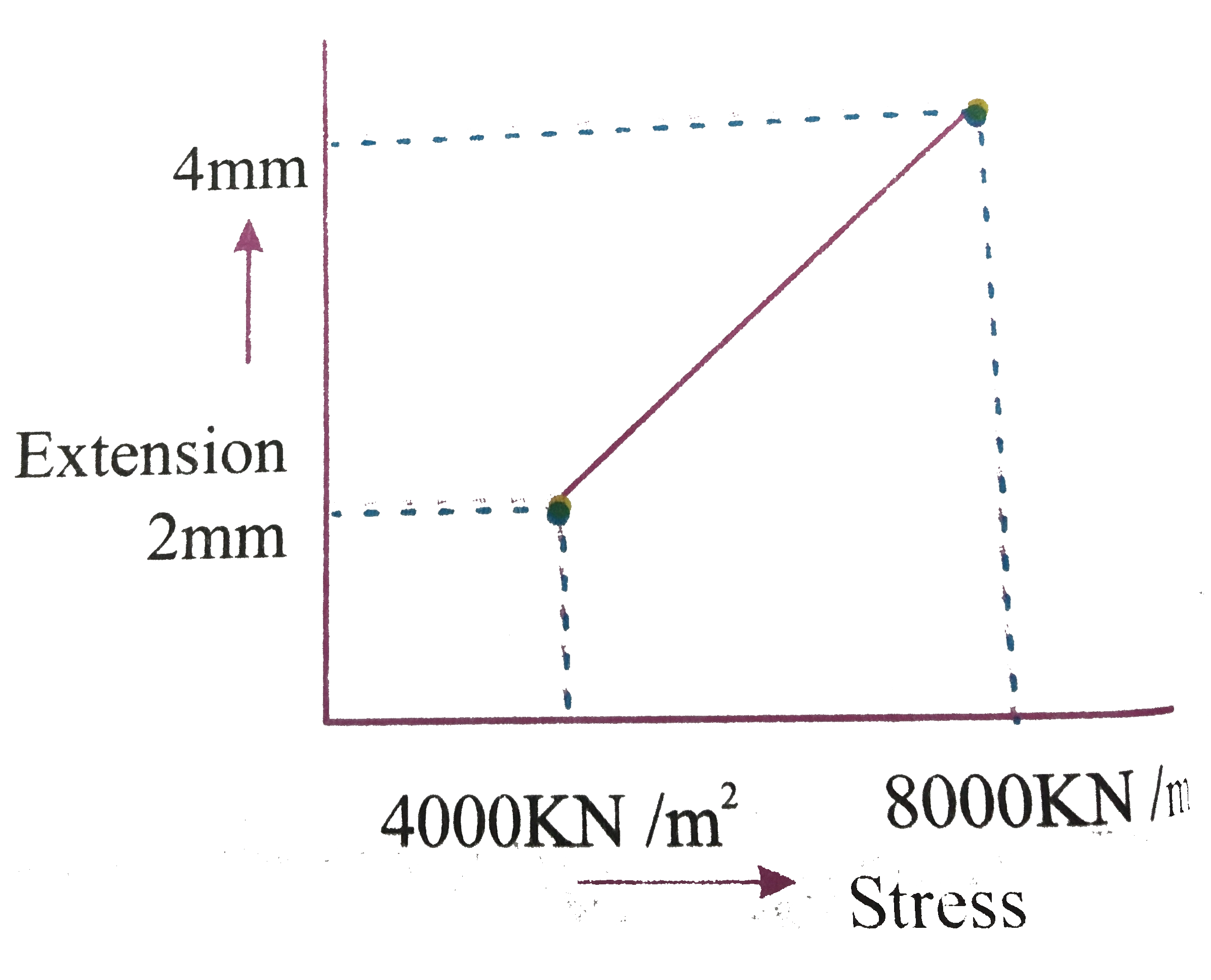
In determine of youggn modulus of ealsticity of wire, a force is applied and extension is recoreded. Initial length of wire $\text{'}1m\text{'}$ . The curce between extension and stress is depicted then young modulus of wire will be:

Options

A. `2 xx 10^(9) N//m^(2)`
B. `1 xx 10^(9) N//m^(2)`
C. `2 xx 10^(10) N//m^(2)`
D. `1 xx 10^(10) N//m^(2)`

Answer

A

Explanation

`Delta lamda = (Fl)/(Ay)`
`(Delta l)/((F//A)) =(l)/(y)` =slope of curve
`(l)/(y)=((4-2)xx10^(-3))/(400 xx 10^(3))`
Given `lamda =1m rarr y = (4000 xx 10^(3))/(2 xx 10^(-3))=2 xx 10^(9) N//m^(2)`.