An ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers of turns per unit length is 1000 turns/meter. The solenoid is fixed and empty from inside. A wooden whell is co-axially to the solenoid and it is free to rotate about its axis of symmetry without any friction. The weeden wheel has radius b = 1m, moment of inertia 1 = 1 kg m2, about its axis of symmetry and is initially stationary. Charge of 1000μC is applied uniformly on the periphery of the wheel. Now the solenoid is connected to a voltage source whose emf varies with time as ε=(2μ0)t volt. Now switch is on at t = 0. Neglect the resistance of the solenoid and mutual-inductance between the wheel and solenoid.

Magnetic field in the solenoid at time t is :
(1000)t2tesla
(2000)2 tesla
(500)2 tesla
(1000)t tesla
The correct Answer is:A
L=didt=emf=2μ0t
(1)∫di=2μ0t=t∫t=0tdt⇒i=1μ0t2
B=μ0ni=(μ0)(1000)(t2μ0)=(1000)t2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.60
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.61
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
An ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers of turns per unit length is 1000 turns/meter. The solenoid is fixed and empty from inside. A wooden whell is co-axially to the solenoid and it is free to rotate about its axis of symmetry without any friction. The weeden wheel has radius b = 1m, moment of inertia 1 = 1 kg m2, about its axis of symmetry and is initially stationary. Charge of 1000μC is applied uniformly on the periphery of the wheel. Now the solenoid is connected to a voltage source whose emf varies with time as ε=(2μ0)t volt. Now switch is on at t = 0. Neglect the resistance of the solenoid and mutual-inductance between the wheel and solenoid.

Angular velocity of the wheel at t = 2 sec. will be :-
View SolutionAn ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers of turns per unit length is 1000 turns/meter. The solenoid is fixed and empty from inside. A wooden whell is co-axially to the solenoid and it is free to rotate about its axis of symmetry without any friction. The weeden wheel has radius b = 1m, moment of inertia 1 = 1 kg m2, about its axis of symmetry and is initially stationary. Charge of 1000μC is applied uniformly on the periphery of the wheel. Now the solenoid is connected to a voltage source whose emf varies with time as ε=(2μ0)t volt. Now switch is on at t = 0. Neglect the resistance of the solenoid and mutual-inductance between the wheel and solenoid.
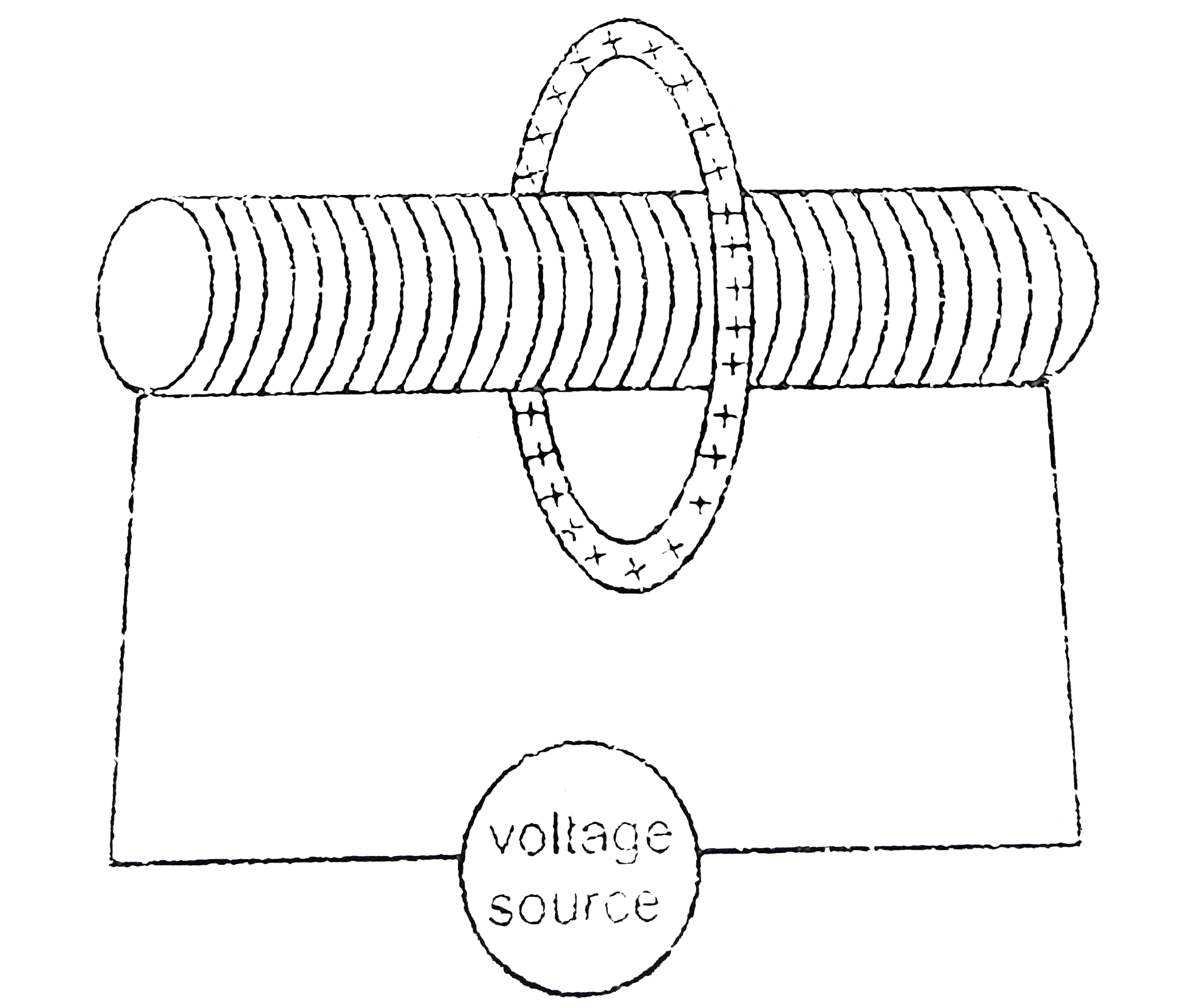
Now at t =2, switch is suddenly off. The angular velocity of the wheel after switching off will be :
View Solution
Knowledge Check
An ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers of turns per unit length is 1000 turns/meter. The solenoid is fixed and empty from inside. A wooden whell is co-axially to the solenoid and it is free to rotate about its axis of symmetry without any friction. The weeden wheel has radius b = 1m, moment of inertia 1 = 1 kg m2, about its axis of symmetry and is initially stationary. Charge of 1000μC is applied uniformly on the periphery of the wheel. Now the solenoid is connected to a voltage source whose emf varies with time as ε=(2μ0)t volt. Now switch is on at t = 0. Neglect the resistance of the solenoid and mutual-inductance between the wheel and solenoid.

Angular velocity of the wheel at t = 2 sec. will be :-A0.5 rad/secB1 rad/secC2 rad/secD4 rad/secAn ideal solenoid of inductance L = 1H. Radius a = 0.5 m and numbers of turns per unit length is 1000 turns/meter. The solenoid is fixed and empty from inside. A wooden whell is co-axially to the solenoid and it is free to rotate about its axis of symmetry without any friction. The weeden wheel has radius b = 1m, moment of inertia 1 = 1 kg m2, about its axis of symmetry and is initially stationary. Charge of 1000μC is applied uniformly on the periphery of the wheel. Now the solenoid is connected to a voltage source whose emf varies with time as ε=(2μ0)t volt. Now switch is on at t = 0. Neglect the resistance of the solenoid and mutual-inductance between the wheel and solenoid.

Now at t =2, switch is suddenly off. The angular velocity of the wheel after switching off will be :AzeroB4 rad/secC2 rad/secD8 rad/secA long solenoid has 800 turns per meter length of solenoid. What is the magnatic induction at the end of the solenoid if it carries a current of 2.5 A?
A6.28×10−4Wb/m2B1.256×10−3Wb/m2C3.14×10−4Wb/m2D5×10−4Wb/m2
A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns, It carries a current of 5 A. What is the magnitude of magnetic field inside the solenoid?
View SolutionA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
View SolutionA solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. The magnetic field inside the solenoid is
View SolutionA solenoid having 500 turns and length 2 m has radius of 2 cm , the self inductance of solenoid
View SolutionA long solenoid has 800 turns per metre length of solenoid A current of 1.6 A flow through it. The magnetic induction at the end of the solenoid on its axis is
View Solution
