A smooth hemisphere of mass m and radius R is at rest. A smooth solid sphere of mass 2m and radius R moving with velocity V0 between two horizontal smooth surfaces separated by a distance slightly greater than 2R as shown in figure. Solid sphere collides with the hemisphere. if coefficient of restitution is 12, then

The speed of hemisphere after collision is V0
The speed of solid sphere after collision is V02
The loss in kinetic energy of the system is 14mV20
The final kinetic energy of hemisphere is 14 th the initial kinetic energy of sphere
The correct Answer is:A, B, C
2MV0=2MV1+MV2
12=e=(V2cosθ−V1cosθ)V0cosθ

V1=(2−e)V23=V02
V2=(1+e)2V03=V0
K.E=122mV20
K.E=122m×V204+12×M×V20
Loss in K.E =14mV20.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.60
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.61
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.58
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Knowledge Check
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A circular rope of weight W and radius r=R2 is resting on a smooth sphere of radius R The tension in rope is
 AW/(π√6)BW/(π√12)CW/(π√10)Dnone of these
AW/(π√6)BW/(π√12)CW/(π√10)Dnone of theseA solid sphere of radius 'r' is rolling with velocity V on a smooth plane. The total kinetic energy of sphere is
A710mv2B34mv2C12mv2D14mv2
A solid sphere of mass M and radius R is initially at rest. Solid sphere is gradually lowered onto a truck moving with constant velocity v0

What is the final speed of the sphere's centre of mass m ground frame when eventually pure rolling sets in
View SolutionA uniform solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling. Then the value of h and speed of ccentre of mass are
View SolutionA solid homogeneous sphere is moving on a rough horizontal surface, partly rolling and partly sliding. During the king of motion of the sphere.
View SolutionA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
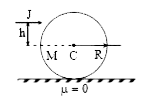
View SolutionA sphere of mass m falls on a smooth hemisphere of mass M resting with its plane face on smooth horizontal table, so that at the moment of impact, line joining the centres makes an angle with the vertical. The velocity of sphere just before impact is u and e is the coefficient of restitution.
View Solution


