A projectile of range R bursts at its highest point in two fragments, Both pieces at the time of bursts have the velocity in the horizontal direction. The heavier is double the mass of the figther. Lighter frangments falls at R2 horizontal distance from the point of projection in the opposite side of projection. The distance. where other part falls, from point of projection.
7R4
5R4
8R4
6R4
The correct Answer is:A
To solve the problem of the projectile that bursts into two fragments at its highest point, we will follow these steps:
Step 1: Understand the Problem
We have a projectile with a range R that bursts into two fragments at its highest point. The heavier fragment has double the mass of the lighter fragment. The lighter fragment falls at a horizontal distance of R2 in the opposite direction from the point of projection.
Step 2: Define the Masses
Let:
- The mass of the lighter fragment be m1.
- The mass of the heavier fragment be m2=2m1.
The total mass of the projectile is:
m=m1+m2=m1+2m1=3m1
Thus, we can express m1 as:
m1=m3,m2=2m3
Step 3: Center of Mass Calculation
At the moment of bursting, the center of mass of the two fragments will continue to move in the same horizontal direction as the original projectile. The position of the center of mass xcm can be expressed as:
xcm=m1⋅(−R2)+m2⋅(R+x)m1+m2
Where x is the distance from the point of projection where the heavier fragment lands.
Step 4: Substitute Known Values
Substituting the values of m1 and m2:
R=m3⋅(−R2)+2m3⋅(R+x)m
Step 5: Simplify the Equation
Multiply through by m to eliminate the denominator:
mR=m3⋅(−R2)+2m3⋅(R+x)
This simplifies to:
mR=−mR6+2mR3+2mx3
Step 6: Combine Like Terms
Rearranging gives:
mR+mR6=2mR3+2mx3
To combine the terms:
6mR+mR6=4mR+2mx3
This simplifies to:
7mR6=4mR+2mx3
Step 7: Solve for x
Cross-multiplying gives:
7mR⋅3=6(4mR+2mx)
This simplifies to:
21mR=24mR+12mx
Rearranging gives:
21mR−24mR=12mx
−3mR=12mx
Dividing by m (assuming m≠0):
−3R=12x
Thus:
x=−3R12=−R4
Step 8: Calculate the Distance from the Origin
The distance where the heavier fragment falls from the point of projection is:
R+x=R−R4=3R4
Final Answer
The distance where the heavier fragment falls from the point of projection is 3R4.
We have a projectile with a range R that bursts into two fragments at its highest point. The heavier fragment has double the mass of the lighter fragment. The lighter fragment falls at a horizontal distance of R2 in the opposite direction from the point of projection.
Let:
- The mass of the lighter fragment be m1.
- The mass of the heavier fragment be m2=2m1.
m=m1+m2=m1+2m1=3m1
Thus, we can express m1 as:
m1=m3,m2=2m3
At the moment of bursting, the center of mass of the two fragments will continue to move in the same horizontal direction as the original projectile. The position of the center of mass xcm can be expressed as:
xcm=m1⋅(−R2)+m2⋅(R+x)m1+m2
Where x is the distance from the point of projection where the heavier fragment lands.
Substituting the values of m1 and m2:
R=m3⋅(−R2)+2m3⋅(R+x)m
Multiply through by m to eliminate the denominator:
mR=m3⋅(−R2)+2m3⋅(R+x)
This simplifies to:
mR=−mR6+2mR3+2mx3
Rearranging gives:
mR+mR6=2mR3+2mx3
To combine the terms:
6mR+mR6=4mR+2mx3
This simplifies to:
7mR6=4mR+2mx3
Cross-multiplying gives:
7mR⋅3=6(4mR+2mx)
This simplifies to:
21mR=24mR+12mx
Rearranging gives:
21mR−24mR=12mx
−3mR=12mx
Dividing by m (assuming m≠0):
−3R=12x
Thus:
x=−3R12=−R4
The distance where the heavier fragment falls from the point of projection is:
R+x=R−R4=3R4
The distance where the heavier fragment falls from the point of projection is 3R4.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.629videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.639videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.609videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
A particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
View Solution
Knowledge Check
- Question 1 - Select One
A ball is projected at an angle 45∘ with horizontal. It passes through a wall of height h at horizontal distance d1 from the point of projection and strikes the ground at a horizontal distance (d1+d2) from the point of projection, then
Ah=2dd_(2)d+d2Bh=d1d2d1+d2Ch=√2d1d2d1+d2Dh=d1d22(d1+d2) - Question 2 - Select One
A projectile, thrown with velocity v0 at an angle α to the horizontal, has a range R. it will strike a vertical wall at a distance R/2 from the point of projection with a speed of
Av0Bv0sinαCv0cosαD√gR2 - Question 3 - Select One
A projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
A60∘Btan−1(12)Ctan−1(√32)D45∘
A projectile is thrown into space so as to have maximum horizontal range R. Taking the point of projection as origin, find out the co-ordinates of the point where the speed of the particle is minimum.
View SolutionA projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)View SolutionA projectile of mass 5m is projected at 40m/s at 75^(@) above horizontal It explodes at highest point into two fragments The smaller part of mass m falls at the point of projection.Where does the other part fall? (distance from point of projection) (A) 60m (B) 40m (C) 100m (D) 80m
View SolutionA particle is projected such that its horizontal range would be R. At the highest point, the particle breaks into two identical parts P and Q. If P comes to rest, the horizontal distance of point from the point of projection (i.e. origin) where the particle Q lands on the ground is
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
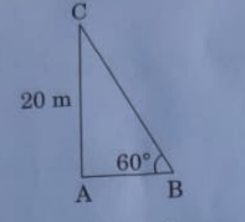 View Solution
View Solution

