A particle is projected such that its horizontal range would be R. At the highest point, the particle breaks into two identical parts P and Q. If P comes to rest, the horizontal distance of point from the point of projection (i.e. origin) where the particle Q lands on the ground is
1.5 R
R
2.5 R
2 R
The correct Answer is:A
To solve the problem, we need to analyze the motion of the particle and the effects of the explosion at its highest point. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
A particle is projected with a horizontal range R. At the highest point of its trajectory, the particle breaks into two identical parts, P and Q. The part P comes to rest, while part Q continues moving.
Step 2: Determine the Velocity at the Highest Point
At the highest point, the vertical component of the velocity is zero, and the horizontal component remains vcosθ, where v is the initial velocity and θ is the angle of projection.
Step 3: Apply Conservation of Momentum
Before the explosion, the total momentum in the horizontal direction is:
m⋅vcosθ
After the explosion, part P has a mass of m2 and comes to rest, while part Q has a mass of m2 and moves with a velocity v1. By conservation of momentum:
m⋅vcosθ=0+m2⋅v1
This simplifies to:
vcosθ=12v1
Thus,
v1=2vcosθ
Step 4: Calculate the Time of Flight for Part Q
The maximum height hmax reached by the particle can be expressed as:
hmax=v2sin2θ2g
The time taken to fall from this height to the ground can be calculated using the equation of motion:
s=ut+12gt2
Here, s=hmax, u=0, and a=g:
v2sin2θ2g=12gt2
Solving for t:
t2=v2sin2θg2
t=vsinθg
Step 5: Calculate the Horizontal Distance Traveled by Part Q
The horizontal distance d traveled by part Q during the time t is given by:
d=v1⋅t
Substituting v1 and t:
d=(2vcosθ)(vsinθg)
d=2v2sinθcosθg
Step 6: Relate the Distance to the Range R
We know that the range R of the projectile is given by:
R=v2sin2θg
Using the identity sin2θ=2sinθcosθ, we can express d in terms of R:
d=2v2sinθcosθg=R2
Step 7: Total Horizontal Distance from the Origin
At the highest point, the particle has traveled a horizontal distance of R2. After the explosion, part Q travels an additional distance of d:
Total distance=R2+d=R2+R2=R
Final Result
The total horizontal distance from the point of projection where part Q lands is:
Distance from origin=R+R2=3R2
Conclusion
Thus, the horizontal distance of point Q from the point of projection is 3R2.
---
A particle is projected with a horizontal range R. At the highest point of its trajectory, the particle breaks into two identical parts, P and Q. The part P comes to rest, while part Q continues moving.
At the highest point, the vertical component of the velocity is zero, and the horizontal component remains vcosθ, where v is the initial velocity and θ is the angle of projection.
Before the explosion, the total momentum in the horizontal direction is:
m⋅vcosθ
After the explosion, part P has a mass of m2 and comes to rest, while part Q has a mass of m2 and moves with a velocity v1. By conservation of momentum:
m⋅vcosθ=0+m2⋅v1
This simplifies to:
vcosθ=12v1
Thus,
v1=2vcosθ
The maximum height hmax reached by the particle can be expressed as:
hmax=v2sin2θ2g
The time taken to fall from this height to the ground can be calculated using the equation of motion:
s=ut+12gt2
Here, s=hmax, u=0, and a=g:
v2sin2θ2g=12gt2
Solving for t:
t2=v2sin2θg2
t=vsinθg
The horizontal distance d traveled by part Q during the time t is given by:
d=v1⋅t
Substituting v1 and t:
d=(2vcosθ)(vsinθg)
d=2v2sinθcosθg
We know that the range R of the projectile is given by:
R=v2sin2θg
Using the identity sin2θ=2sinθcosθ, we can express d in terms of R:
d=2v2sinθcosθg=R2
At the highest point, the particle has traveled a horizontal distance of R2. After the explosion, part Q travels an additional distance of d:
Total distance=R2+d=R2+R2=R
The total horizontal distance from the point of projection where part Q lands is:
Distance from origin=R+R2=3R2
Thus, the horizontal distance of point Q from the point of projection is 3R2.
Similar Questions
A particle is projected with a velcity (u) so that its horizontal range isthrice the greatest heitht attained. What is its horizontal range?
View SolutionA particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View Solution
Knowledge Check
- Question 1 - Select One
In figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
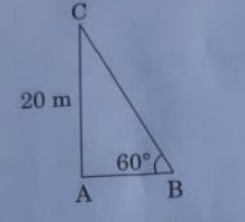 A200mB250mC150mD50m
A200mB250mC150mD50m - Question 2 - Select One
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
A3R4B3R2C5R4D3R - Question 3 - Select One
A particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
A2R3B7R6C5R4Dnone of these
A body of mass m is projected from ground for horizontal range R. At the highest point it is fragmented into two identical parts. If one parts returns back to the point of projection, then other part will have the horizontal range
View SolutionA particle is projected at 60(∘) to the horizontal with a kinetic energy K . The kinetic energy at the highest point is
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View SolutionA particle is projected at 60∘ to the horizontal with kinetic energy K. Its kinetic energy at the highest point is :
View SolutionA particle just clear a wall of height b at a distance a and strikes the ground at a distance from the point of projection, the angle of projection is :
View Solution

