A disc of mass m is connected with an ideal spring of spring constant k inside a lift as shown. The left starts moving with constant acceleration . At the same moment disc starts rolling without sliding on the wall of lift (from rest). If spring is in natural length initially then friction force acting on disc as a function of y is given by : (y is the displacement of the disc with respect to lift)

The correct Answer is:C
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.65
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.66
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.63
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
Knowledge Check
A disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:
 AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθk
AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθkA solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
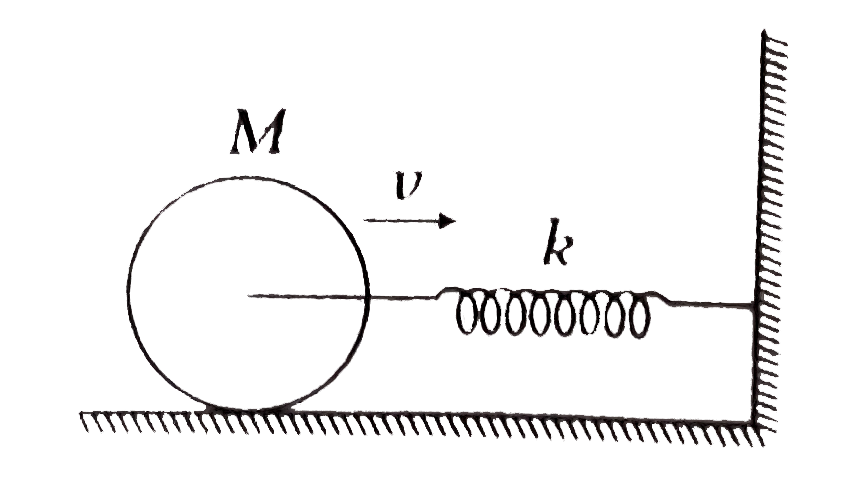 Av√2M3kBv√2M5kCv√5k7MDv√7M5k
Av√2M3kBv√2M5kCv√5k7MDv√7M5kA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
 A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
A solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
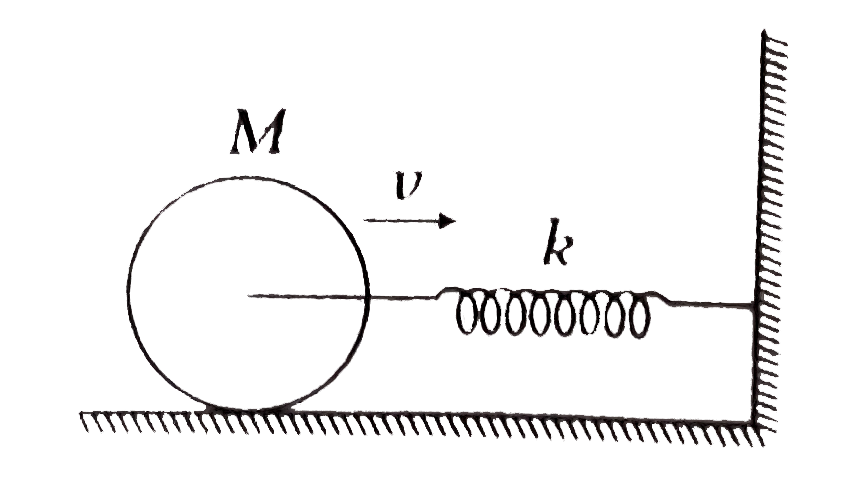
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionA spring balance and a physical balance are kept in a lift. In these balance equal masses are placed. If now the lift starts moving upward with constant acceleration, then.
View SolutionA spring balance and a physical balance are kept in a lift. In these balance equal masses are placed. If now the lift starts moving upward with constant acceleration, then.
View SolutionA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:

View Solution
