The given system is displacement by distance 'A' and released. Both the blocks (each of mass m) move together without relative slipping in the whole process. The magnetic of frictionless force between them at time 't' is
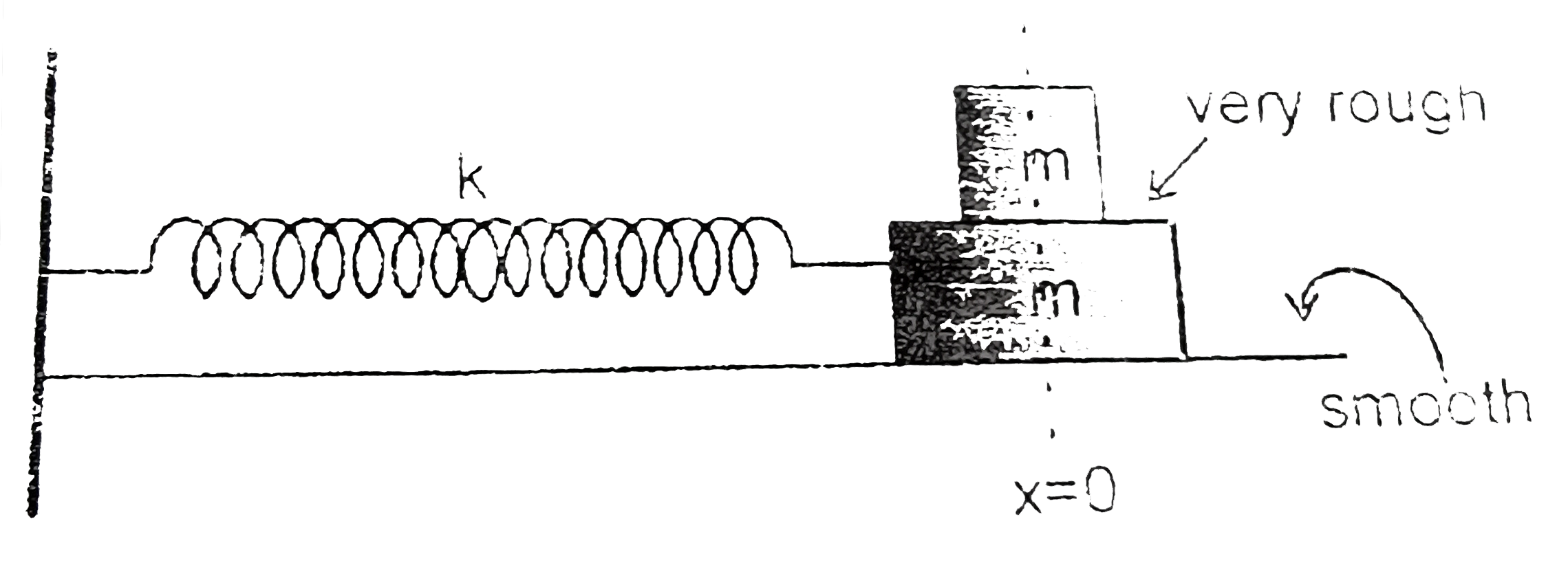
where ω=√K2m
KA2[cosωt]
KA2cosωt
KA2[sinωt]
KA[cosωt]
The correct Answer is:A
a=ω2x
a=Kx2m=KA2mcosωt
f=ma=∣∣∣KA2cosωt∣∣∣.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.67
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.68
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.65
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
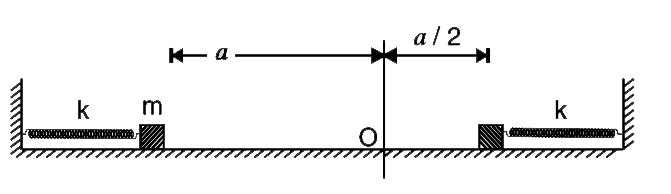
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.

View SolutionTwo point particles of mass m and 2m are initially separated by a distance 4a. They are then released to become free to move. Find the velocities of both the particles when the distance between them reduces to a.
View Solution
Knowledge Check
When distance between two given magnetic poles is halved, force between them becoems k times, where k=
A1B2C4D1/4A block P of mass m is placed on a smooth horizontal surface. A block Q of the same mass is placed over the block P and the coefficient of static friction between them is μ. A spring of spring constant K is attached to block Q. The blocks are displaced together to a distance A and released. The upper block oscillates without slipping over the lower block. The maximum frictional force between the block is:
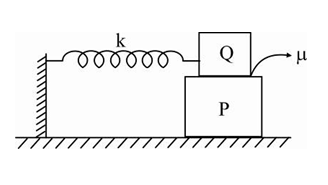 AzeroBKAC12KADμmg
AzeroBKAC12KADμmgTwo blocks each of mass m are joined together using an ideal spring of force constant K and natural length l0 . The blocks are touching each other when the system is released from rest on a rough horizontal surface. Both the blocks come to rest simultaneously when the extension in the spring is l04. The coefficient of friction between each block and the surface (assuming it to be same between any of the blocks and the surface) is :
AKl040mgBKl08mgC3Kl08mgD1720Kl0mg
Two blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K=800N/m and the system is placed on a horizontal surface as shown.
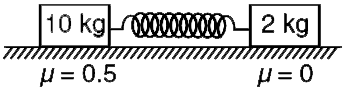
The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move.
View SolutionBlock B of mass m has been placed on block A of mass 3 m as shown. Block A rests on a smooth horizontal table. F1 is the maximum horizontal force that can be applied on the block A such that there is no slipping between the blocks. Similarly, F2 is the maximum horizontal force that can be applied on the block B so that the two blocks move together without slipping on each other. When F1andF2 both are applied together as shown in figure.

(a) Find the friction force acting between the blocks.
(b) Acceleration of the two blocks.
(c) If F2 is decreased a little, what will be direction of friction acting on B.
View SolutionFour identical blocks each of mass m are linked by threads as shown. If the system moves with constant acceleration under the influence of force F, the tension T2 is

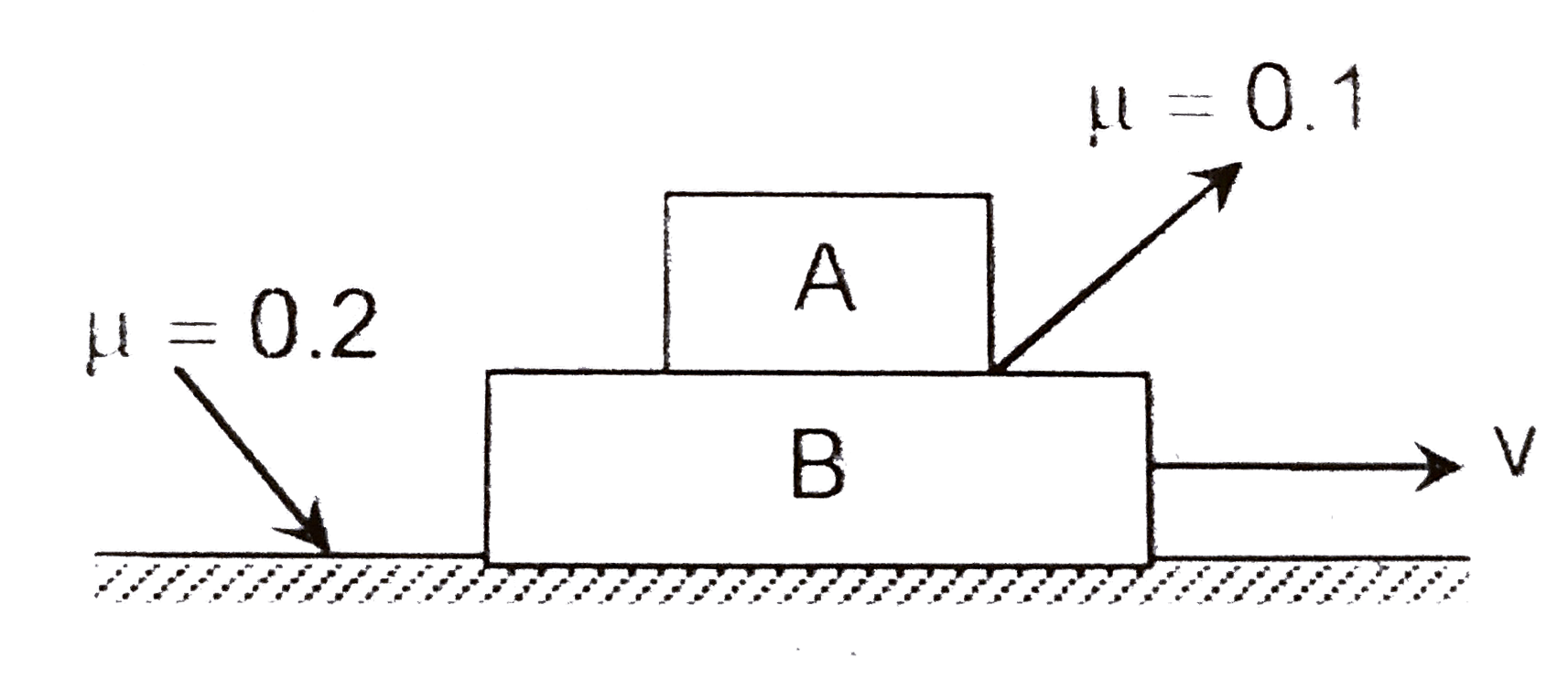
View SolutionBoth the blocks as shown in figure are given together a horizontal velocity towards right. The acceleration of the centre of mass of the system of block is (mA=2mB=2kg).
View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.

View Solution
