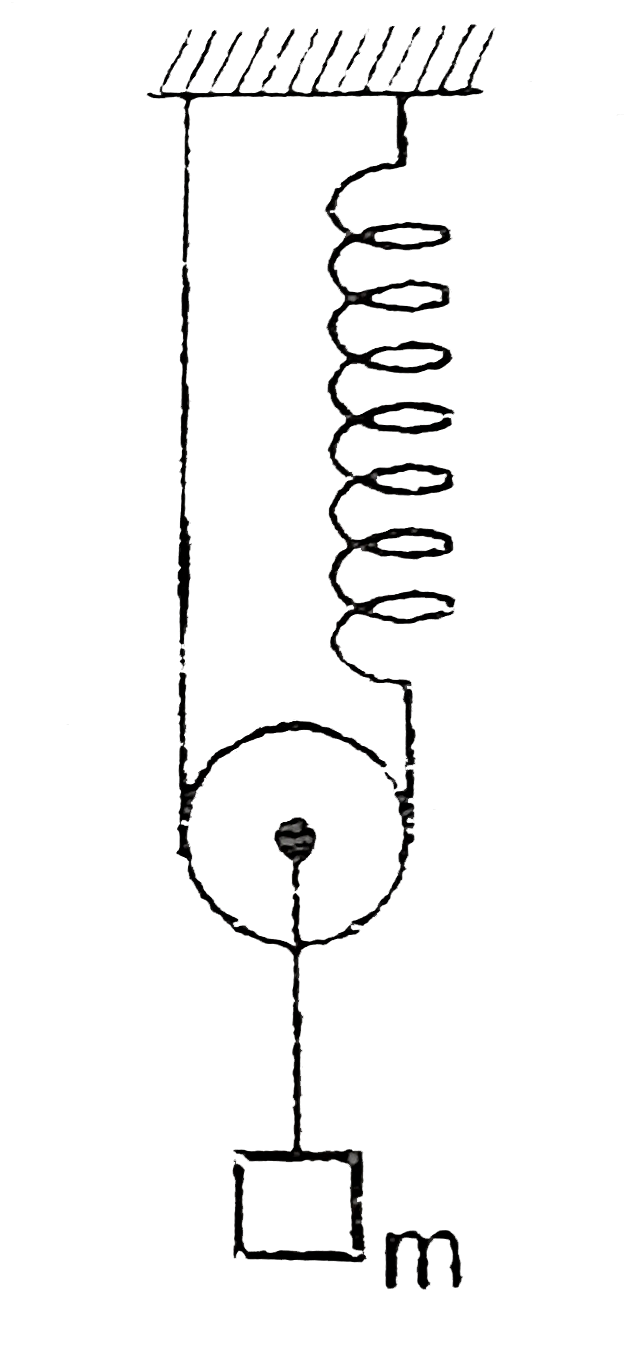
The system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
1 m
12m
2 m
2.5 m
The correct Answer is:A
Let maximum elongation in spring be X, then block descends through x2
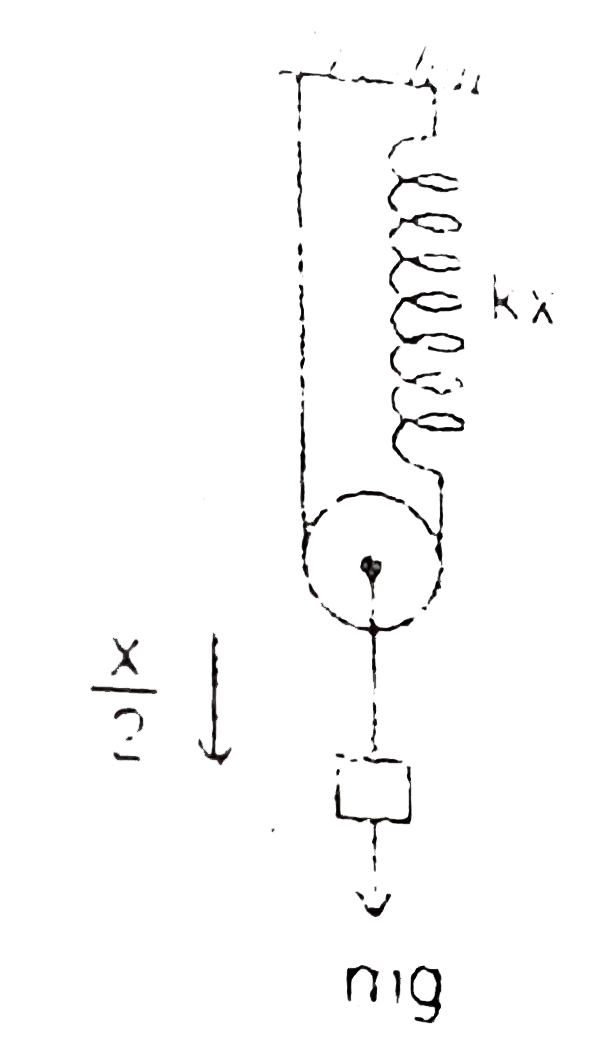
BY WET
mgx2−12kx2=0⇒X=mgk=10×10100=1m
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6710videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.689videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.659videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
In the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
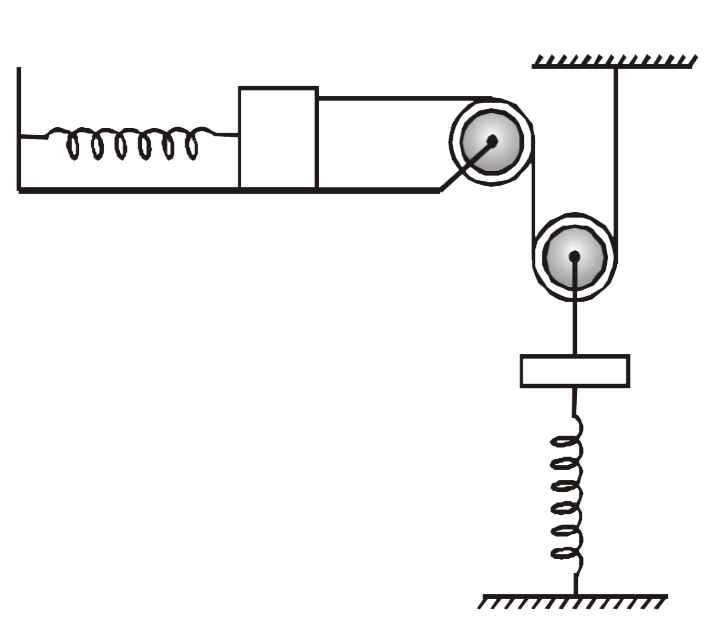
Maximum speed of the block placed horizontally is:View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
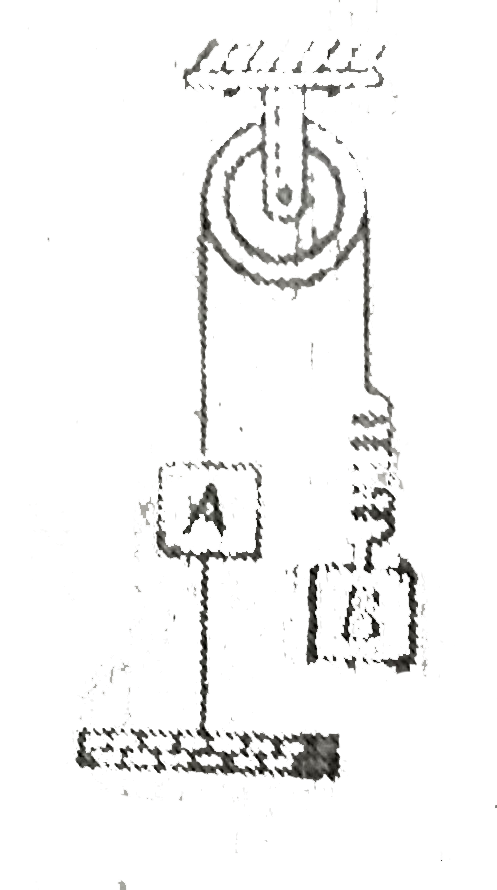 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
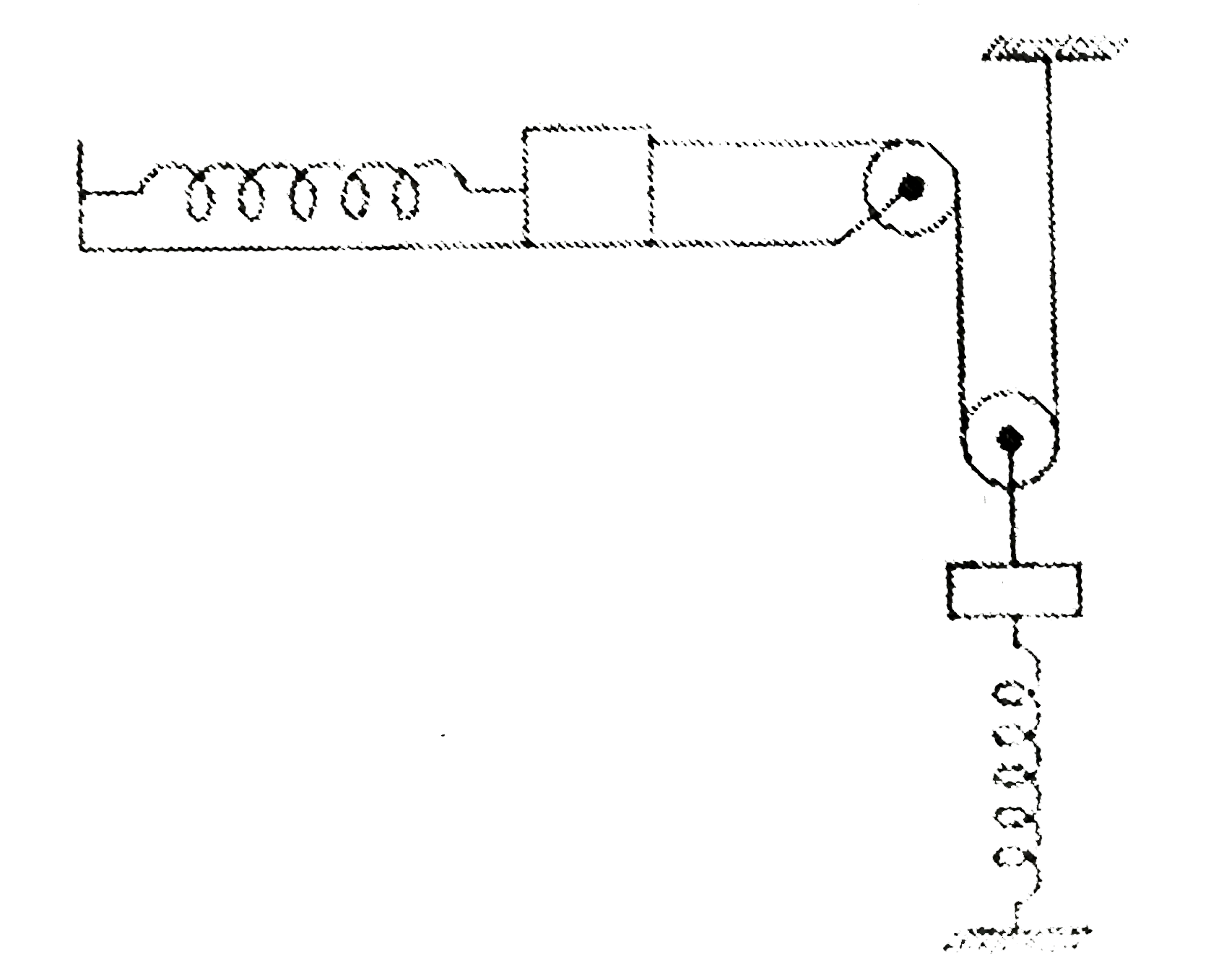
Extension of horizontal spring in equilibrium isA0.2 mB0.4 mC0.6 mD0.8 m - Question 2 - Select One
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m. Extension of horizontal spring in equilibrium is:
 A0.2mB0.4mC0.6mD0.8m
A0.2mB0.4mC0.6mD0.8m - Question 3 - Select One
Initially spring is in natural length and both blocks are in rest condition. Then deter mine
maximum extension in spring . K = 20 N/MA203cmB103cmC403cmD193cm
Two blocks of masses m1=2kg and m2=4kg are attached to two ends of a light ideal spring of force constant k = 1000 N/m. The system is kept on a smooth inclined plane inclined at 30∘ with horizontal. The block m2 is attached to a light string whose other end is connected to a mass m3=1kg. A force F = 15N is applied on m1 and the system is released from rest. Assume initially the spring is at relaxed position and the system is released from rest. Find the
(a) maximum extension of the spring.
(
 View Solution
View SolutionConsider the situation shown in figure.
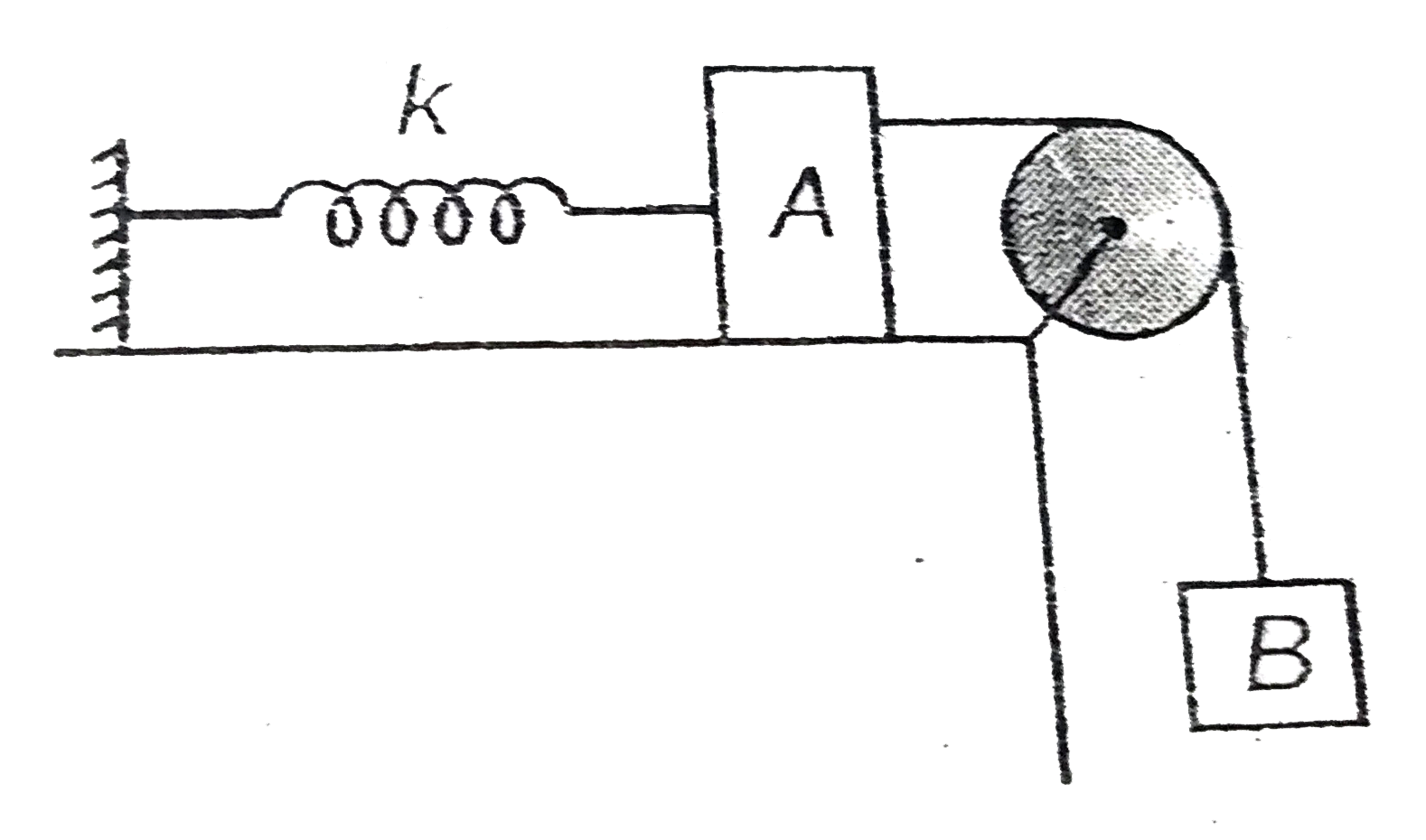
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.View SolutionThe system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
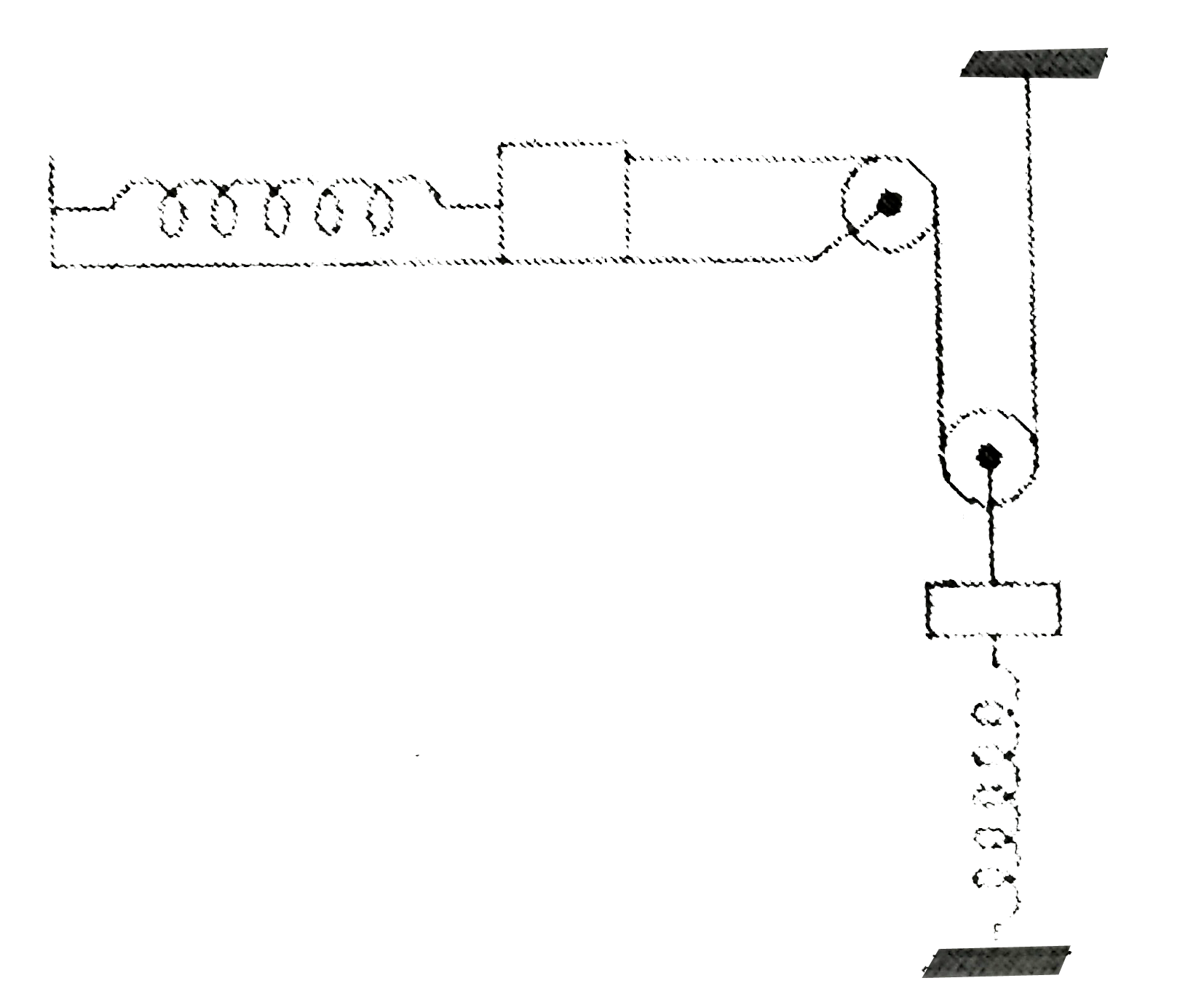
In the equilibrium position, speed of the block placed horizontally isView SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 View Solution
View SolutionA block of mass 2M is attached to a massless spring with spring-constant k. This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0 Which of the following option(s) is(are) correct? [g is the acceleration due to gravity. Neglect friction]
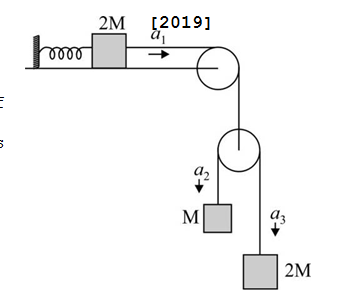 View Solution
View Solution

