A weight w is to be moved from the bottom to the top of an inclined plane of inclination θ to the horizontal. If a smaller force is to be applied to drag it along the plane in comparison to lift it vertically up, the coefficient of friction should be such that.
μ>tan(π2−θ2)
μ<tan(π2−θ2)
μ<tanθ
μ>tan.π4
The correct Answer is:B
F1=wsinθ+μwcosθ
F2=w
As, F1<F2
∴μ<tan(π4−θ2)
Topper's Solved these Questions
Similar Questions
A ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA ball is dropped from the height h on an inclined plane of inclination θ. If the coefficient of restitution is e, at what distance along the plane , the ball again collides with the plane.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ - Question 2 - Select One
A block is released from the top of an inclined plane of inclination θ. Its velocity at the bottom of plane is v. If it slides down a rough inclined plane of the same inclination , its velocity at bottom is v/2. The coefficient of friction is
A34cosθB14cosθC14tanθD34tanθ - Question 3 - Select One
A block of weight w rests on a horizontal plane. A force P inclined at an angle theta to the plane is applied to the block until it is on the of motion. Find the value of coefficient of friction.
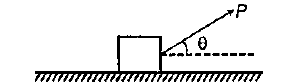 Apsinθ(psinθ−ω)Bpcosθ(ω−psinθ)Cpcosθ(psinθ−ω)Dpsinθ(ω−psinθ)
Apsinθ(psinθ−ω)Bpcosθ(ω−psinθ)Cpcosθ(psinθ−ω)Dpsinθ(ω−psinθ)
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
 View Solution
View SolutionA disc of mass m slides with the zero initial velocity down an inclined plane of inclination θ to the harizontal, having traveled the distance d along the horizontal plane, the disc stops. Find the work performed by the friction over the whole distance, assuming the friction coefficient μ for both the inclined and horizontal planes.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friction is μ)
View SolutionWhat is the time required for a block to slide down from the top to the bottom ofan inclined plane 6.4 m long if the inclination of the plane with the horizonta l is 30° and the coefficient of friction= 0.2?
View Solution

