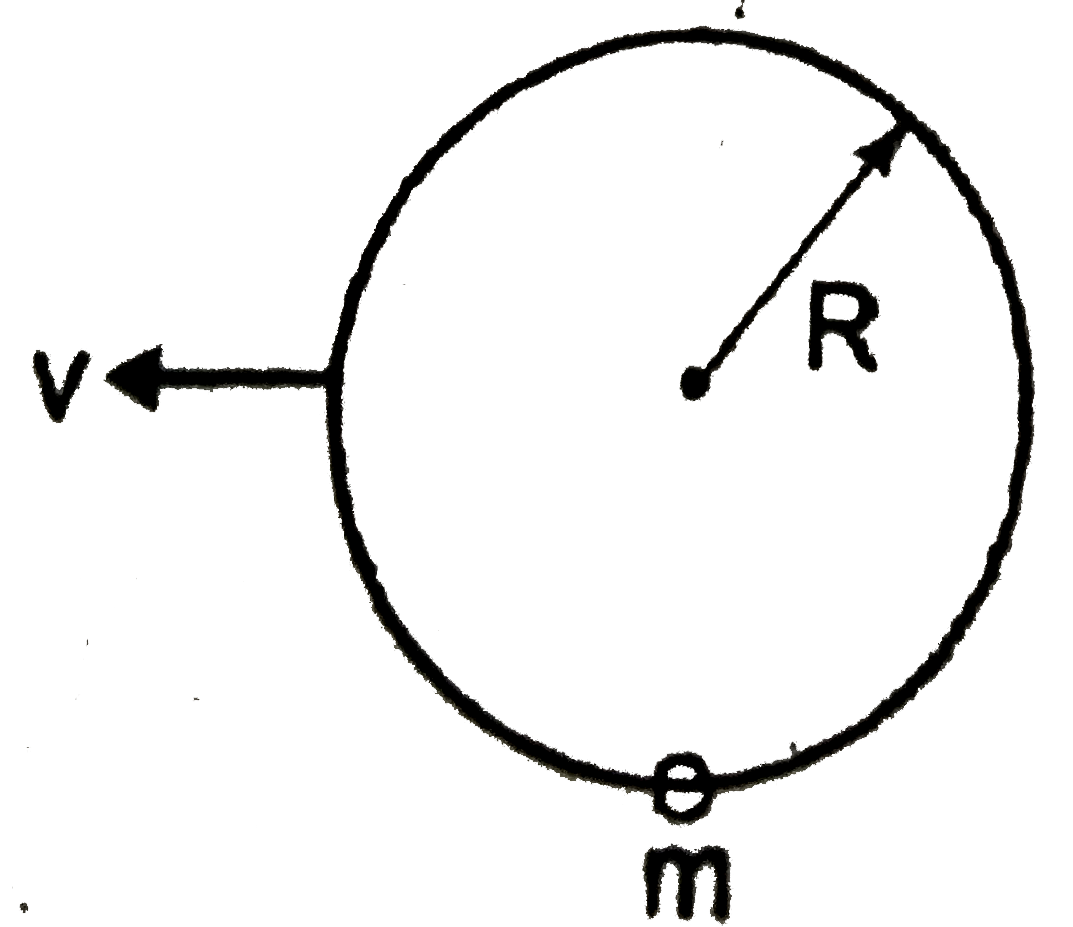
A ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
√3gR
√4gR
√5gR
√5.5gR
The correct Answer is:B
In the frame of ring (inertial w.r.t earth), the initial velocity of the bead is v at the lowest position.
The condition for bead to complete the vertical circle is, its speed at top position
vtop≥0
From conservation of energy
12mv2top+mg(2R)=12mv2
or v=√4gR
Topper's Solved these Questions
Similar Questions
A massless ring hangs from a thread and two beads of mass m slide it without friction. The beads are released simultaneously from the top of the ring and slide down along possible sides. Find the angle from vertical at which the ring will start to rise.
View SolutionA ring of mass M hangs from a thread and two beads of mass m slides on it without friction. The beads are released simultaneously from the top of the ring and slides down in opposite sides. Show that the ring will start to rise, if m>3M2 . ltbr>
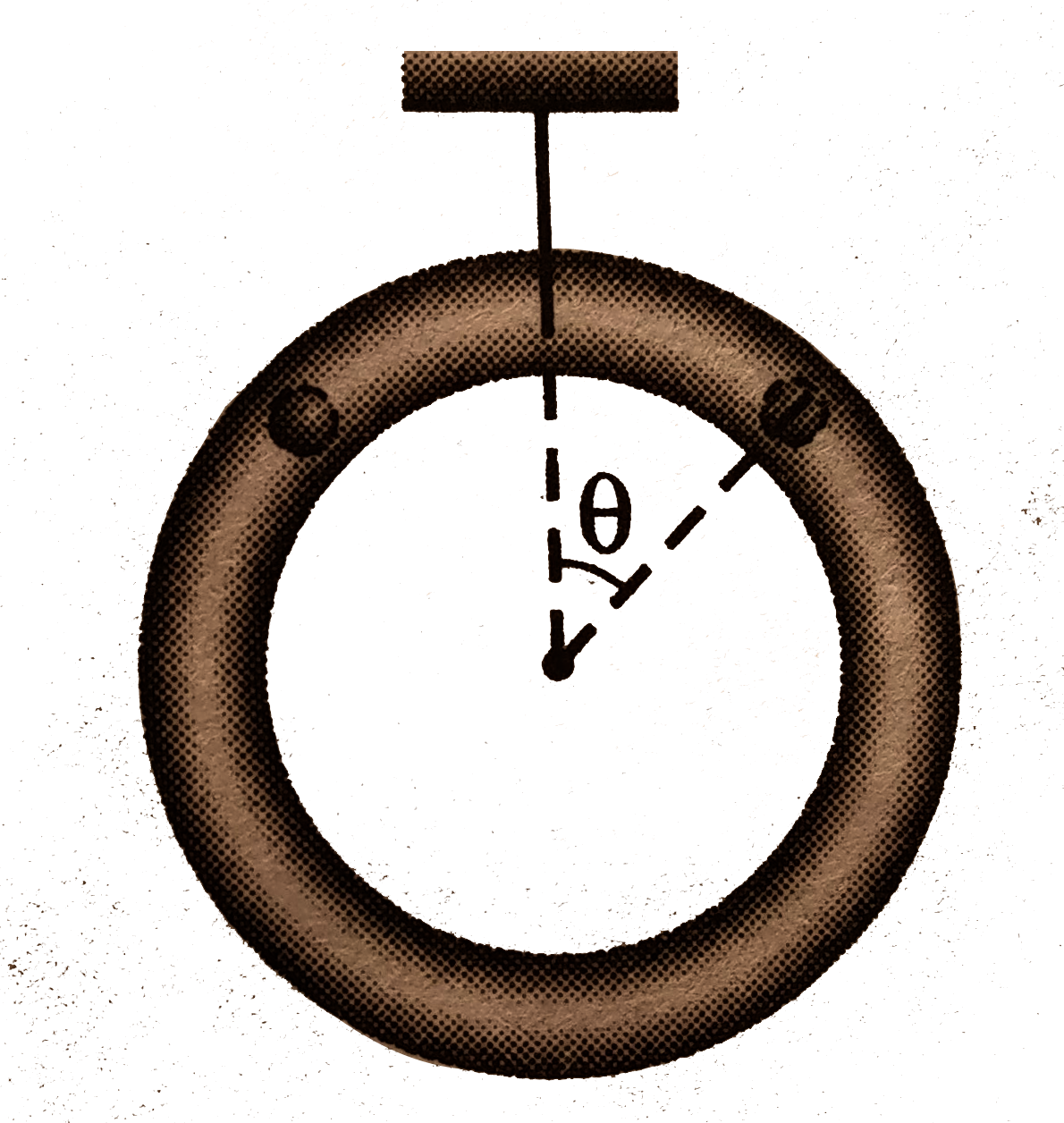View Solution
Knowledge Check
- Question 1 - Select One
A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
zAgsinαB(g+a0)sinαCgsinα+a0cosαDgsinα−a0cosα - Question 2 - Select One
A ring of radius 4a is rigidly fixed in vertical position on a table. A small disc of mass m and radius a is released as shown in the fig. When the disc rolls down, without slipping, to the lowest point of the ring, then its speed will be
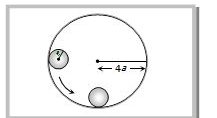A√gaB√2gaC√3gaD√4ga - Question 3 - Select One
A ring of radius R is rolling purely on the outer surface of a pipe of radius 4R At some instant the center of the ring has constant speed =v then the acceleration of the point on the ring which is in contact with the surface of the pipe is
A4v2/5RB3v2/5RCv2/4RDzero
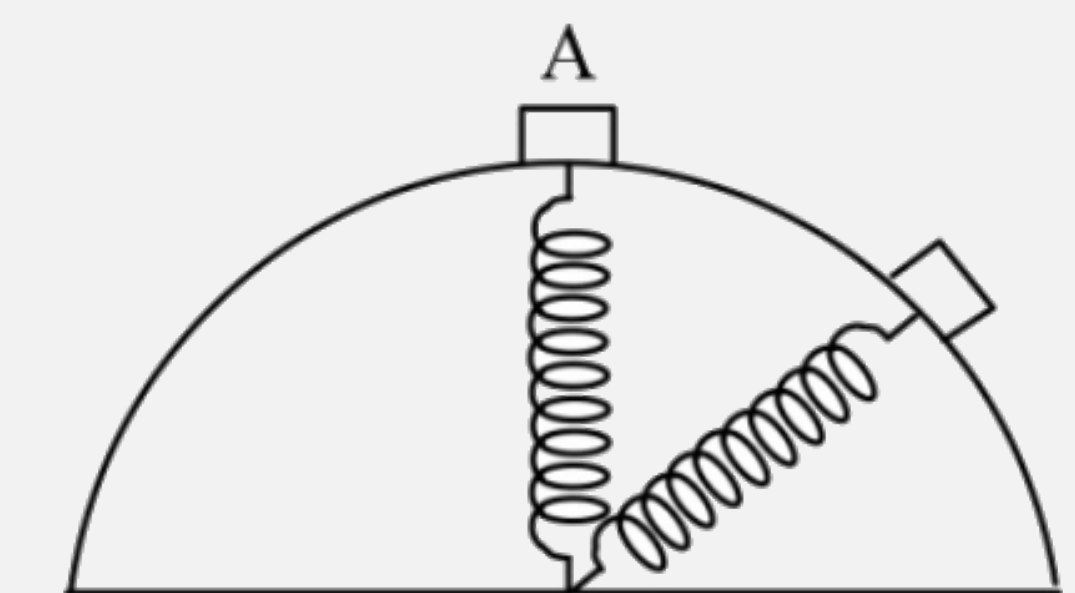
The figure shows a thin ring of mass M=1kg and radius R=0.4m spinning about a vertical diameter (take I=12MR2) A small beam of mass m=0.2kg can slide without friction along the ring When the bead is at the top of the ring the angular velocity is 5rad/s What is the angular velocity when the bead slips halfwat to θ=45∘?View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View SolutionAn isolated smooth ring of mass M = 2m with two small beads each of mass m is as shown in the figure. Initially both the beads are at diametrically opposite points and have velocity v0 (for each) in same direction. The speed of the beads just before they collide for the first time is (complete system is placed on a smooth horizontal surface and assume each point of ring is touching the surface)
View SolutionA bead of mass m moves on a rod without friction. Initially the bead is at the middle of the rod and the rod moves translationally in a vertical plane with an acceleration a0 in a direction forming angle θ with the horizontal as shown in the given figure. The acceleration of bead with respect to rod is
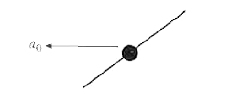View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View Solution