In S.H.M., potential energy (U) V/s, time (t) . Graph is
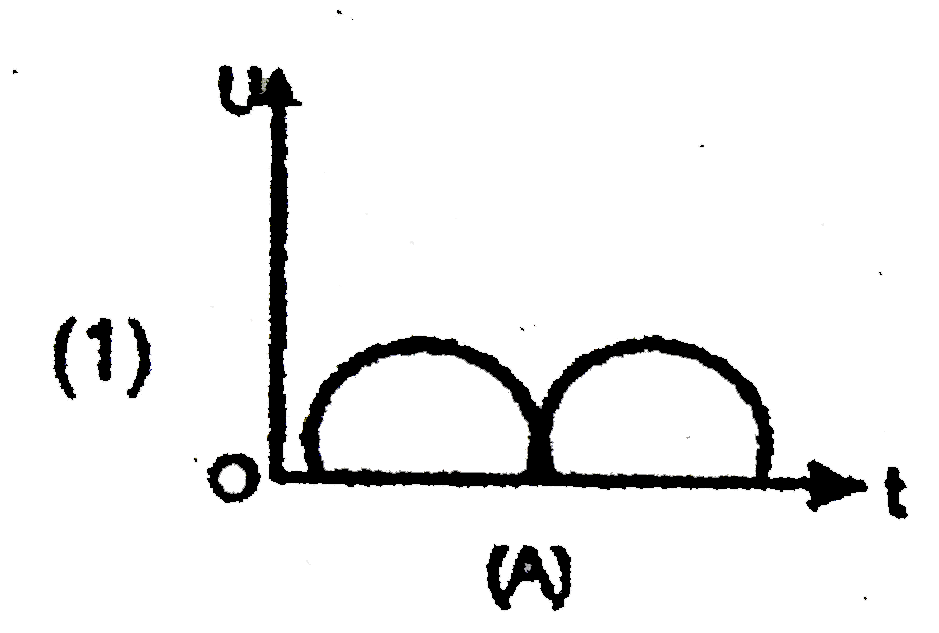
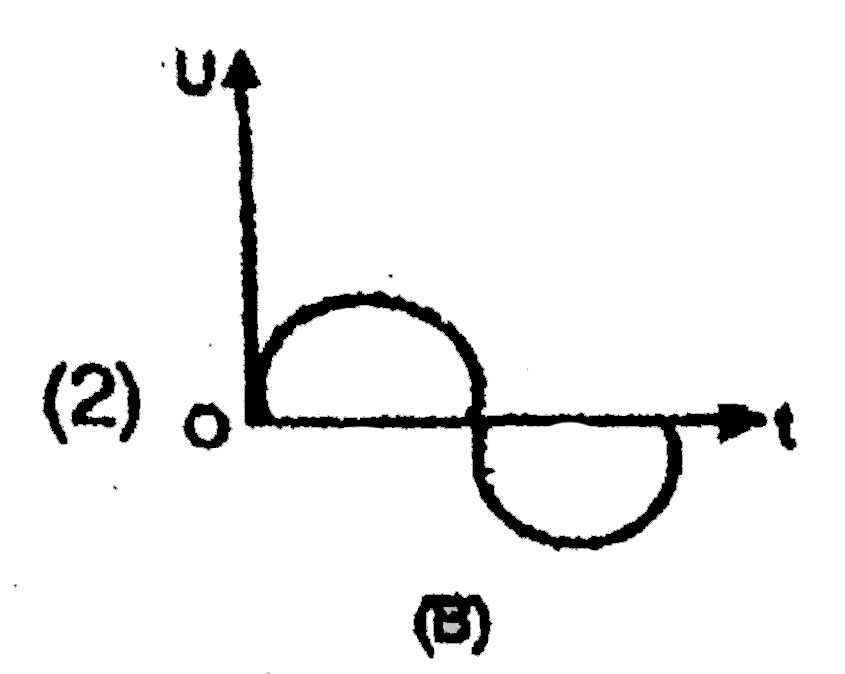


The correct Answer is:A
To determine the potential energy versus time graph for a particle undergoing simple harmonic motion (S.H.M.), we can follow these steps:
1. Understand the Equation of S.H.M.:
The displacement x of a particle in S.H.M. can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
2. Potential Energy in S.H.M.:
The potential energy U of a particle in S.H.M. is given by:
U=12kx2
where k is the spring constant.
3. Substituting the Displacement:
Substitute the expression for x(t) into the potential energy formula:
U(t)=12k(Asin(ωt+ϕ))2
This simplifies to:
U(t)=12kA2sin2(ωt+ϕ)
4. Analyzing the Graph:
The term 12kA2 is a constant. The potential energy U(t) is proportional to sin2(ωt+ϕ). The graph of sin2(x) oscillates between 0 and 1, meaning U(t) will oscillate between 0 and 12kA2.
5. Graph Characteristics:
- The graph will always be above the time axis (since sin2 is always non-negative).
- If ϕ=0, the graph starts at U=0 when t=0.
- If ϕ is not zero, the graph will be shifted horizontally.
6. Final Graph:
The resulting graph of potential energy versus time will be a sinusoidal wave that oscillates between 0 and 12kA2, resembling a sine squared function.
The displacement x of a particle in S.H.M. can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
The potential energy U of a particle in S.H.M. is given by:
U=12kx2
where k is the spring constant.
Substitute the expression for x(t) into the potential energy formula:
U(t)=12k(Asin(ωt+ϕ))2
This simplifies to:
U(t)=12kA2sin2(ωt+ϕ)
The term 12kA2 is a constant. The potential energy U(t) is proportional to sin2(ωt+ϕ). The graph of sin2(x) oscillates between 0 and 1, meaning U(t) will oscillate between 0 and 12kA2.
- The graph will always be above the time axis (since sin2 is always non-negative).
- If ϕ=0, the graph starts at U=0 when t=0.
- If ϕ is not zero, the graph will be shifted horizontally.
The resulting graph of potential energy versus time will be a sinusoidal wave that oscillates between 0 and 12kA2, resembling a sine squared function.
Topper's Solved these Questions
Similar Questions
A time varying voltage V= 2t (Volt) is applied across and ideal inductor of inductance L =2H as shown in Fig. Then (assume current to be zero at t =0)
 View Solution
View SolutionWhich of the following graph is correct between kinetic energy E, potential energy (U) and height (h) from the ground of the partical
View Solution
Knowledge Check
- Question 1 - Select One
When the displacement of a particle in S.H.M. is 0.2m, its Potential energy is equal to 2 J. The force constant of the S.H.M. is
A100N/mB50N/mC200N/mD25N/m - Question 2 - Select One
For a particle executing S.H.M., the kinetic energy K is given K=K0cos2ωt. The maximum value of potential energy is:
AK0BzeroCK0/2Dnot abtainable - Question 3 - Select One
Which of the following graph is correct between kinetic energy E, potential energy (U) and height (h) from the ground of the partical
A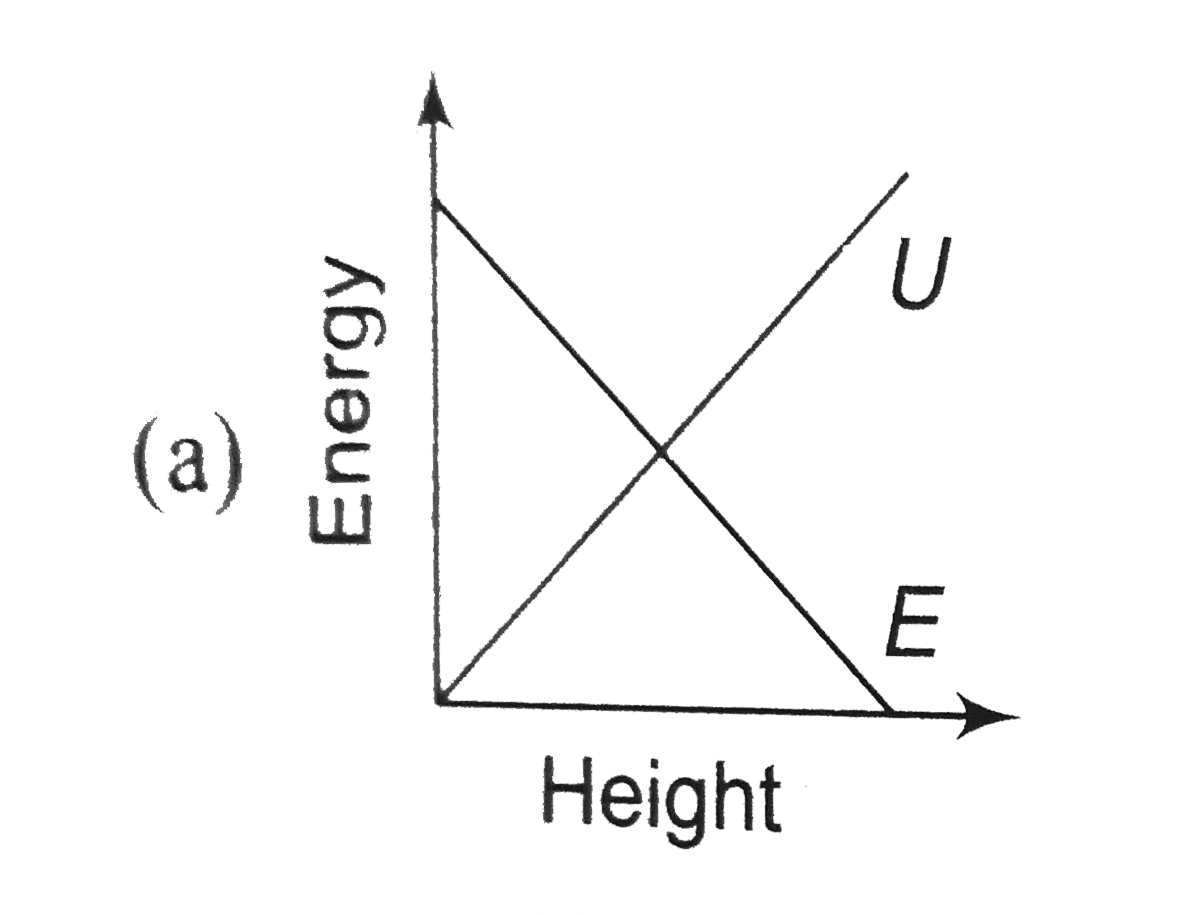 B
B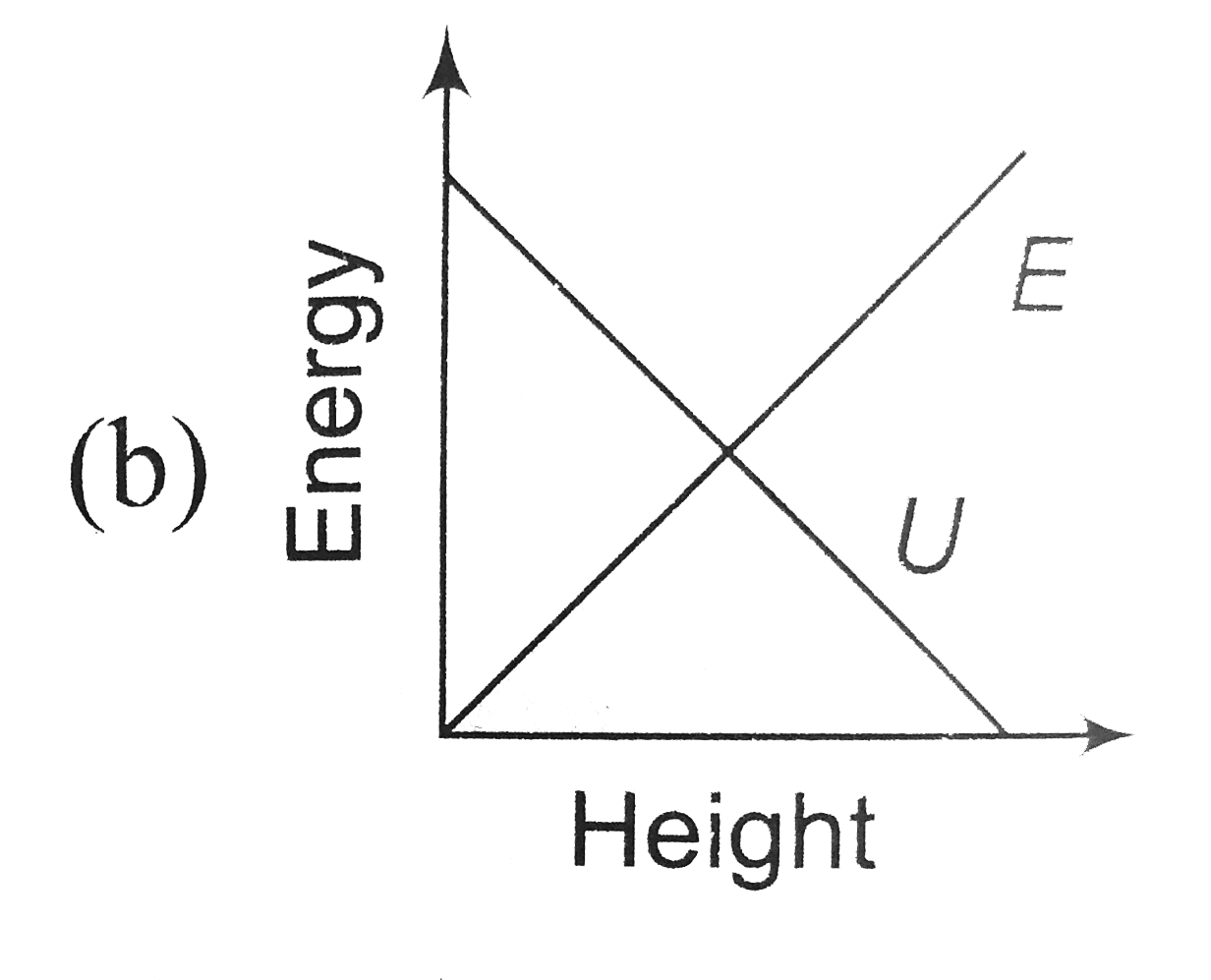 C
C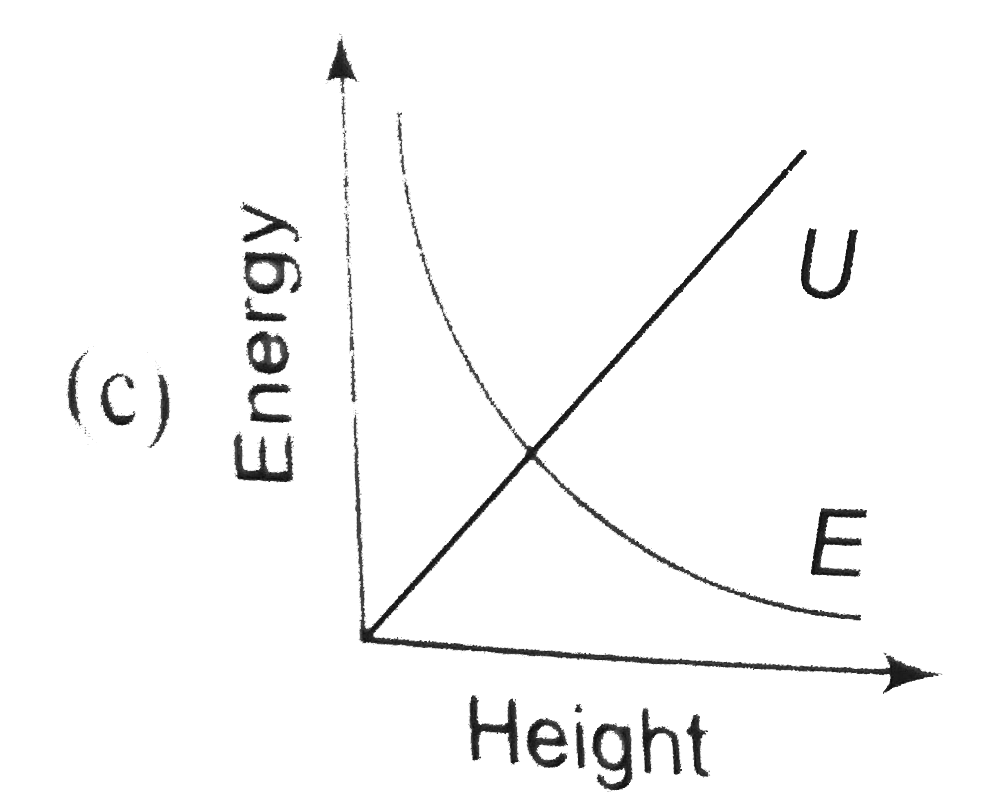 D
D
As a body performs SHM its potential energy U. varies with time as indicated in
View SolutionIn S.H.M., the graph between kinetic energy K and time 't' is
View SolutionA body performs S.H.M. Its kinetic energy K varies with time t as indicated by graph
View SolutionAt the surface of earth, potential energy of a particle is U and potential is V.Change in potential energy and potential at height h=R are suppose ΔU and ΔV.Then
View SolutionThe potential energy of a particle perfonning S.H.M. is
View Solution

