As a body performs SHM its potential energy U. varies with time as indicated in
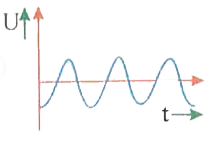
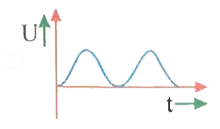

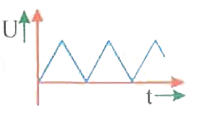
The correct Answer is:B
To solve the problem, we need to analyze how the potential energy U of a body performing Simple Harmonic Motion (SHM) varies with time.
1. Understanding Potential Energy in SHM:
The potential energy U in SHM is given by the formula:
U=12kx2
where k is the spring constant and x is the displacement from the mean position.
2. Displacement in SHM:
In SHM, the displacement x can be expressed as:
x=Asin(ωt)
where A is the amplitude, ω is the angular frequency, and t is time.
3. Substituting Displacement into Potential Energy:
Substitute the expression for x into the potential energy formula:
U=12k(Asin(ωt))2
This simplifies to:
U=12kA2sin2(ωt)
4. Relating Spring Constant to Mass and Angular Frequency:
We know that the spring constant k is related to the mass m and angular frequency ω by:
k=mω2
Substituting this into the potential energy equation gives:
U=12mω2A2sin2(ωt)
5. Analyzing the Function:
The function sin2(ωt) varies between 0 and 1 as t changes. At t=0, sin(0)=0, so U=0. The potential energy reaches its maximum when sin2(ωt)=1.
6. Graph of Potential Energy:
The graph of U as a function of time t will be a sinusoidal wave squared, which is an even function. This means it will be symmetric about the vertical axis and will oscillate between 0 and its maximum value.
7. Conclusion:
Based on the analysis, we can conclude that the potential energy U varies with time in a sinusoidal manner, specifically as U∝sin2(ωt).
The potential energy U in SHM is given by the formula:
U=12kx2
where k is the spring constant and x is the displacement from the mean position.
In SHM, the displacement x can be expressed as:
x=Asin(ωt)
where A is the amplitude, ω is the angular frequency, and t is time.
Substitute the expression for x into the potential energy formula:
U=12k(Asin(ωt))2
This simplifies to:
U=12kA2sin2(ωt)
We know that the spring constant k is related to the mass m and angular frequency ω by:
k=mω2
Substituting this into the potential energy equation gives:
U=12mω2A2sin2(ωt)
The function sin2(ωt) varies between 0 and 1 as t changes. At t=0, sin(0)=0, so U=0. The potential energy reaches its maximum when sin2(ωt)=1.
The graph of U as a function of time t will be a sinusoidal wave squared, which is an even function. This means it will be symmetric about the vertical axis and will oscillate between 0 and its maximum value.
Based on the analysis, we can conclude that the potential energy U varies with time in a sinusoidal manner, specifically as U∝sin2(ωt).
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - II (H.W)
Explore 19 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - III
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - I (H.W)
Explore 66 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
Knowledge Check
A body performs S.H.M. Its kinetic energy K varies with time t as indicated by graph
A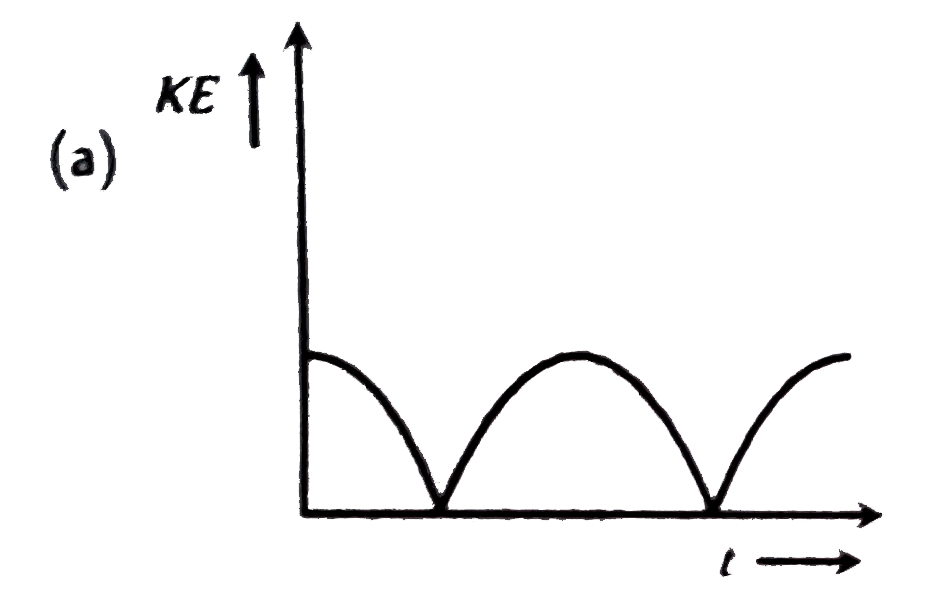 B
B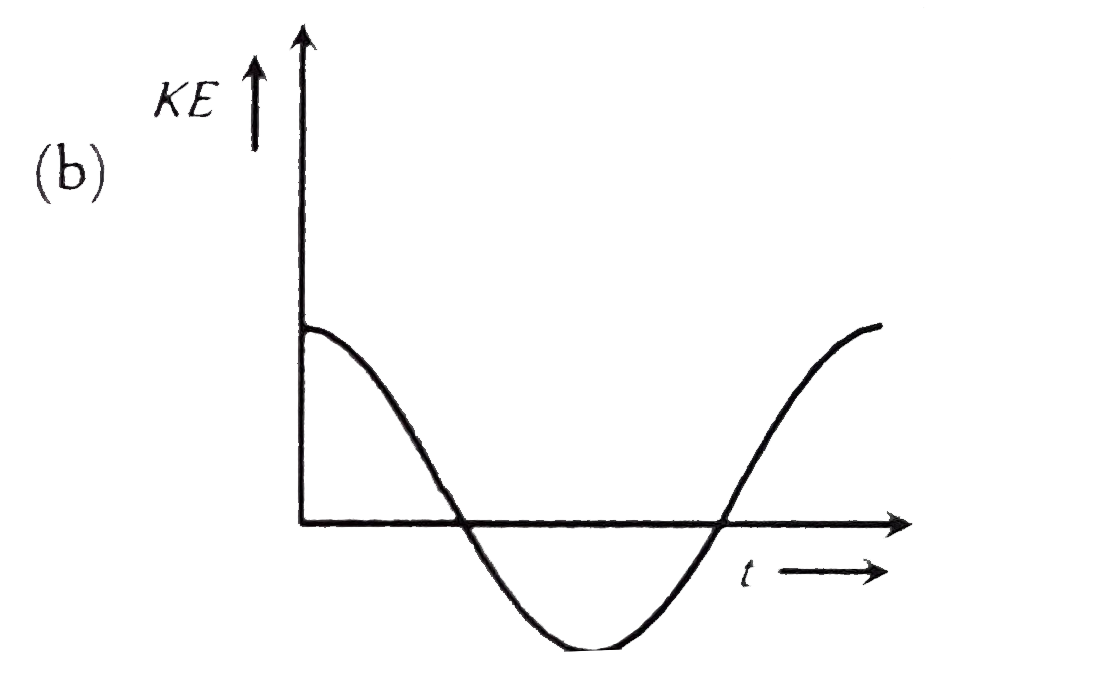 C
C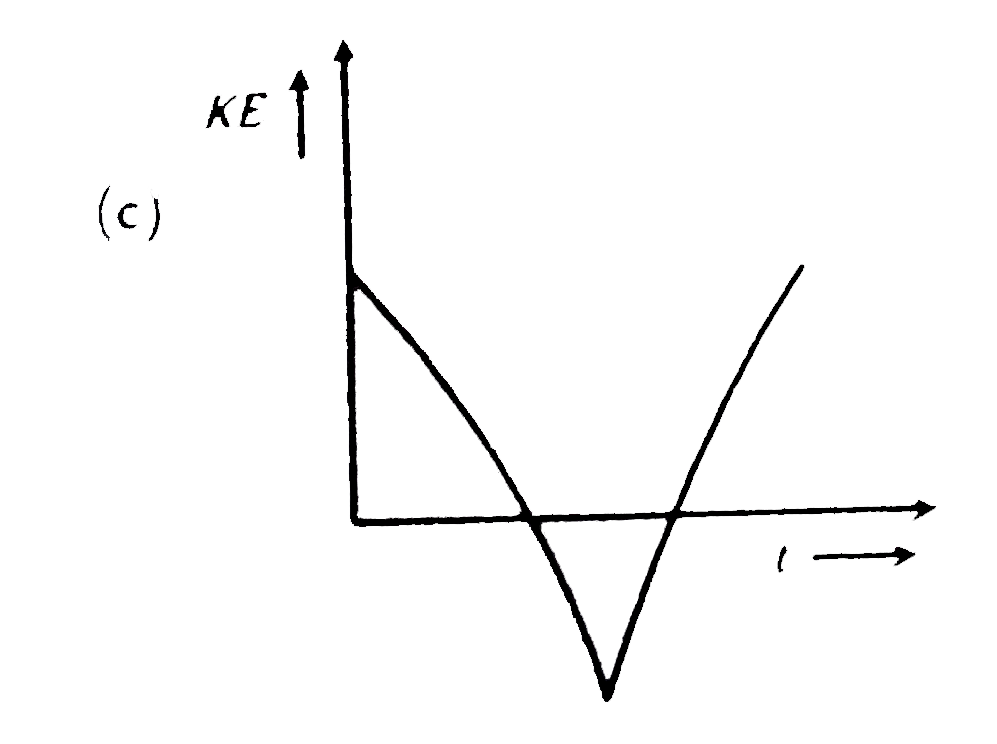 D
D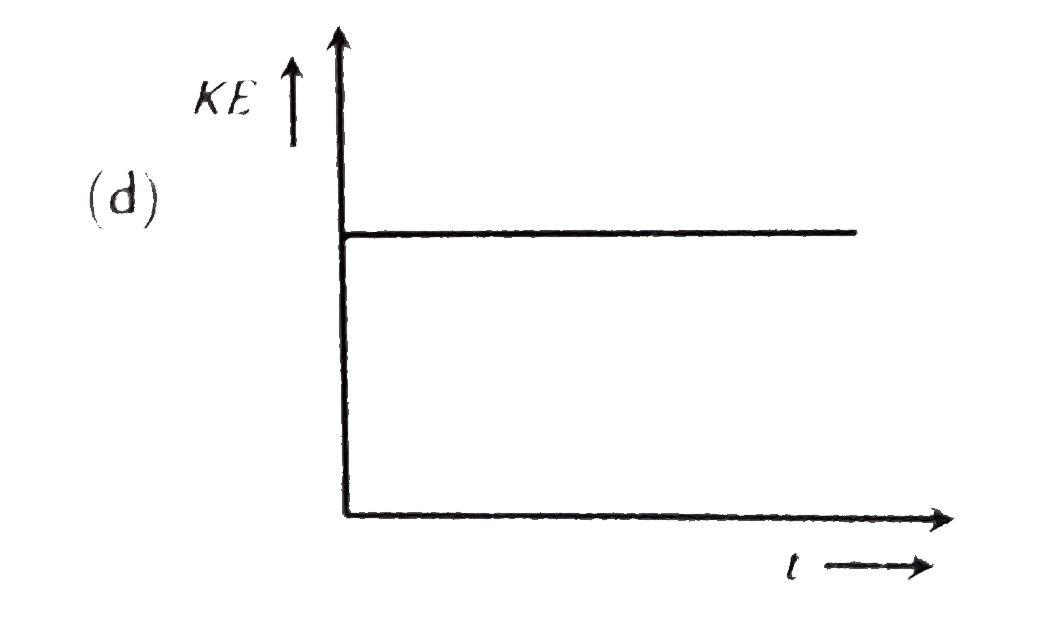

A particle is performing SHM. Its kinetic energy K varies with time t as shown in the figure. ThenA
Period of oscillation of the particle is equal to T.Bexcess potential energy U of the particle varies with time t as shown in Fig.Cexcess potential energy U of the particle varies with time t as shown in fig.Dnone of theseA body is performing SHM, then its
Aaverage total energy per cycle is equal to its maximum kinetic energyBaverage kinetic energy per cycle is equal to half of its maximum kinetic energyCmean velocity over a complete cycle is equal to 2π times of its maximum velocityDroot meqan square velocity is 1√2 times of its maximum velocity
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View Solutionwhen a body performs a U.C .M Its tangential acceleration is
View SolutionIn S.H.M., potential energy (U) V/s, time (t) . Graph is
View SolutionFor a body its elastic potential energy is equal to
View SolutionWhen a particle performs S.H.M., its kinetic energy varies periodically. If the frequency of the particle is 10, then the kinetic energy of the particle will vary with frequency equal to
View Solution