A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
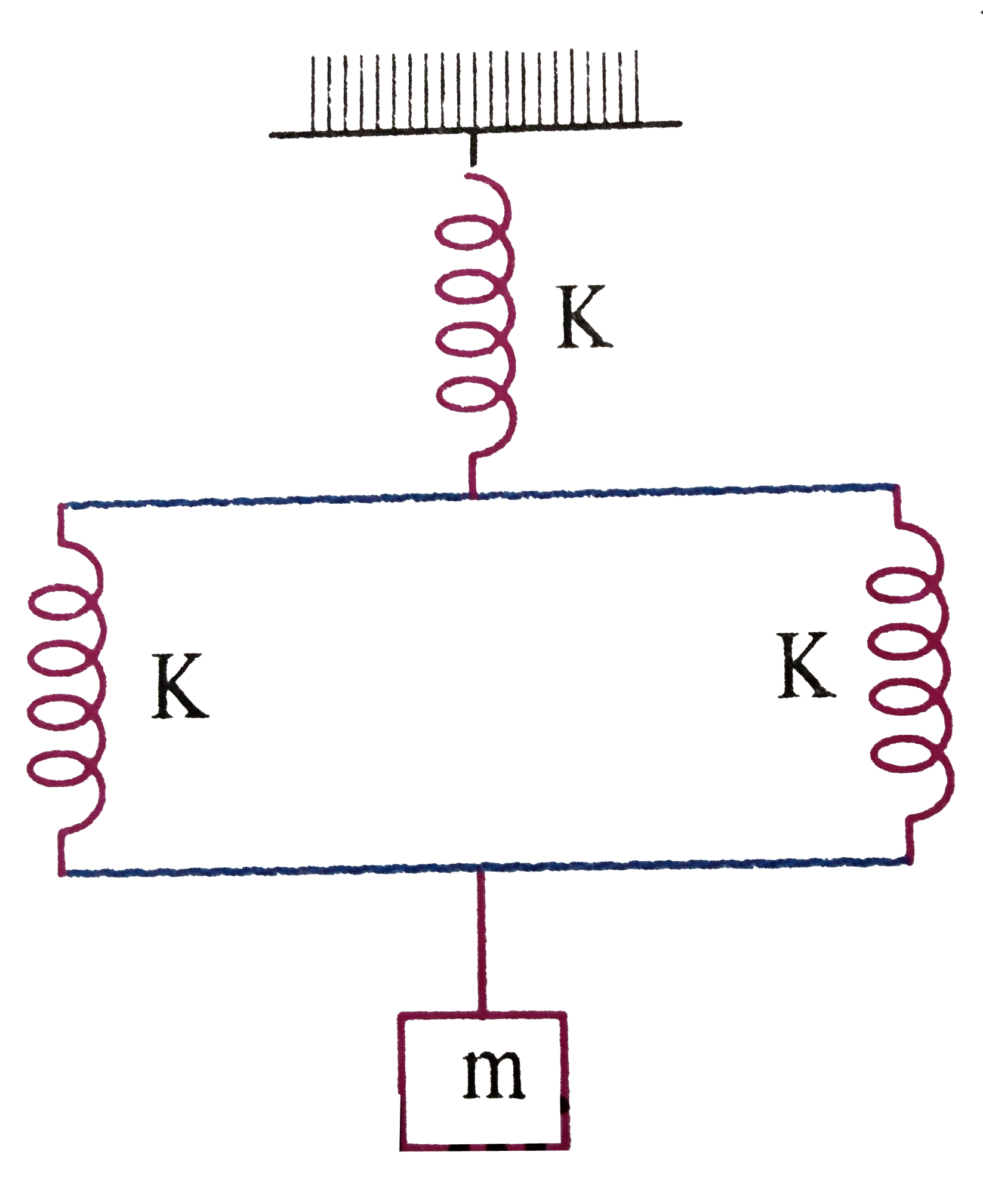
2π√m3k
2π√3m2k
2π√2m3k
2π√3km
The correct Answer is:B
Using series and parallel combination of spring
T=2π√3m2k
Topper's Solved these Questions
Similar Questions
A block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
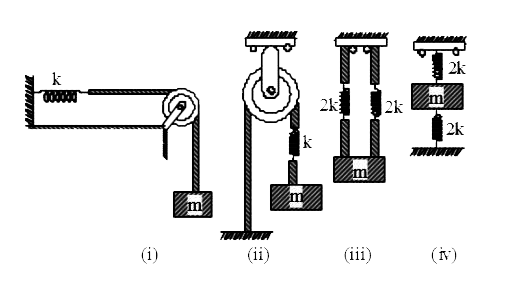
View SolutionA block of mass m is suspended by different springs of force constant shown in figure. Let time period of oscillation in these four positions be T1,T2,T3andT4 Then -
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km - Question 2 - Select One
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4 - Question 3 - Select One
A pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
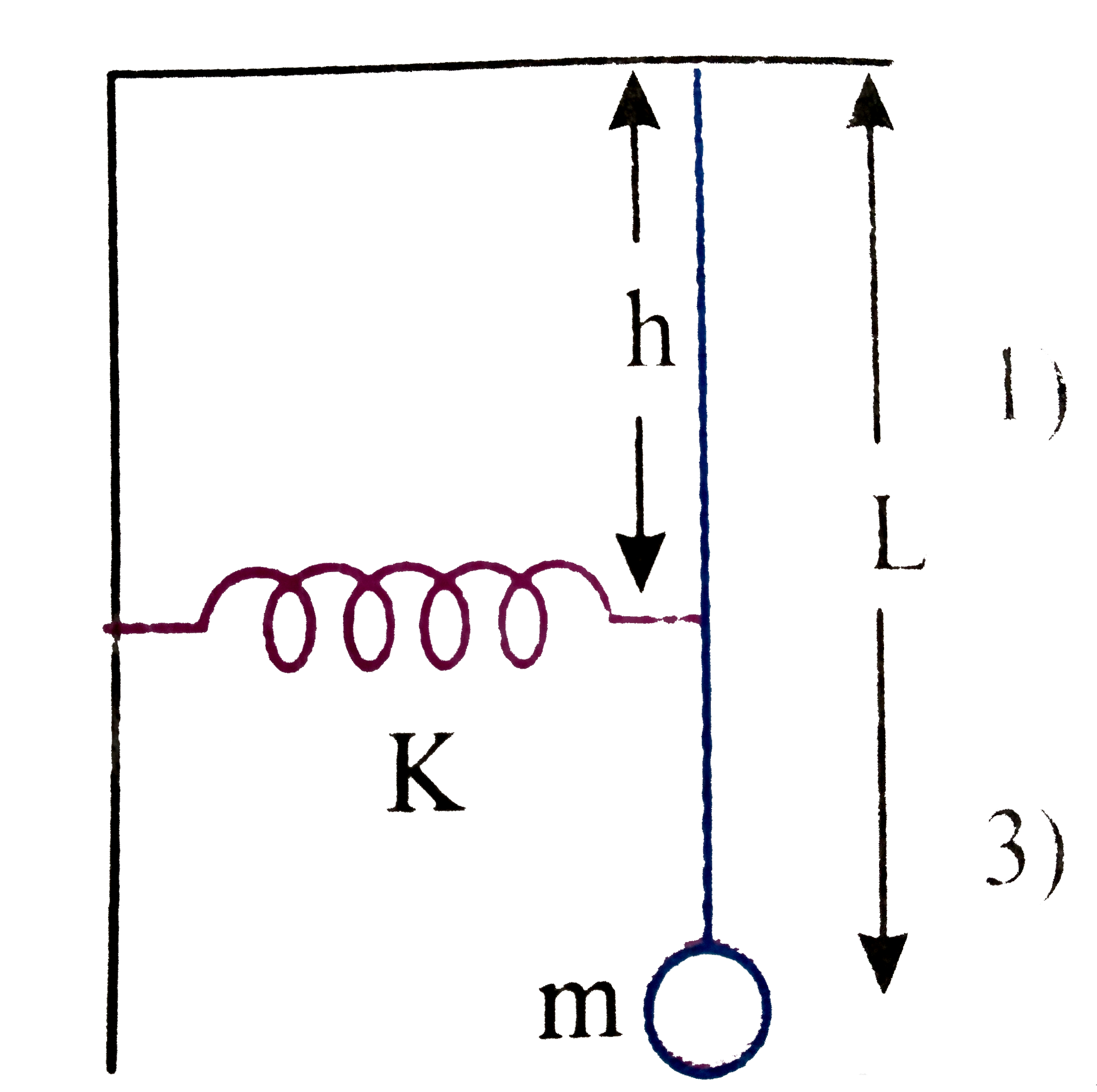 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
Find the period of the oscillations of the devices shown in figure if m is displaced slightly.
 View Solution
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
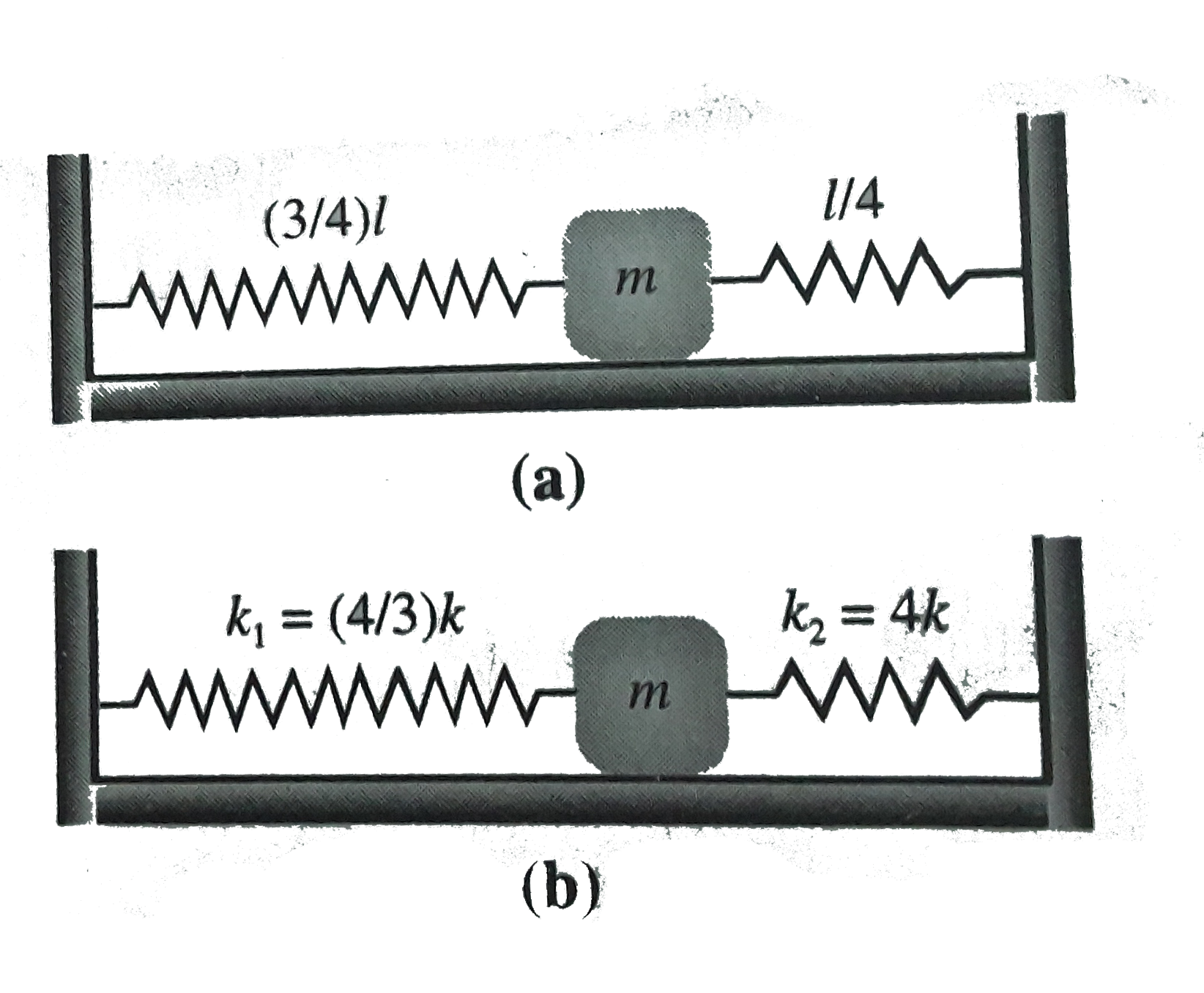 View Solution
View Solutionfigure (a) and (b) represent spring- block system. If m is displacement slightly , find the time period of oscillation of the system.
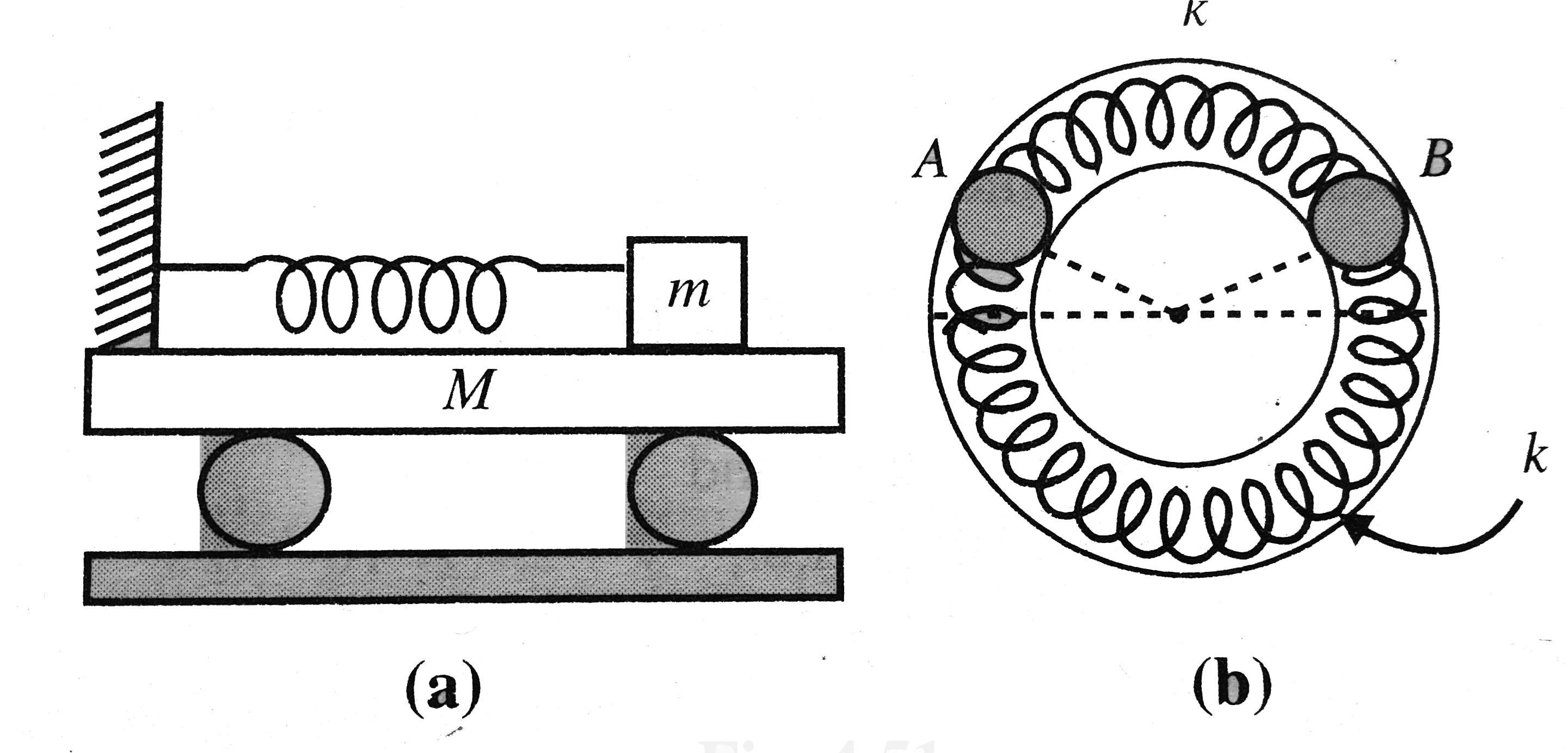 View Solution
View SolutionA block of mass m is suspended by different springs of force constant shown in figure Let time period of oscillation in these four positions be T1,T2,T3 and T4. Then :
 View Solution
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 View Solution
View Solution

