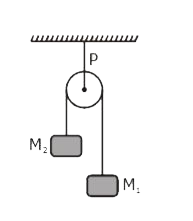
Simple Atwood Machine as System of Particles
The system shown in the figure is known as simple Atwood machine. Initially the masses are held at rest and then let free. Assuming mass m2 more than the mass m1, find acceleration of mass center and tension in the string supporting the pulley.
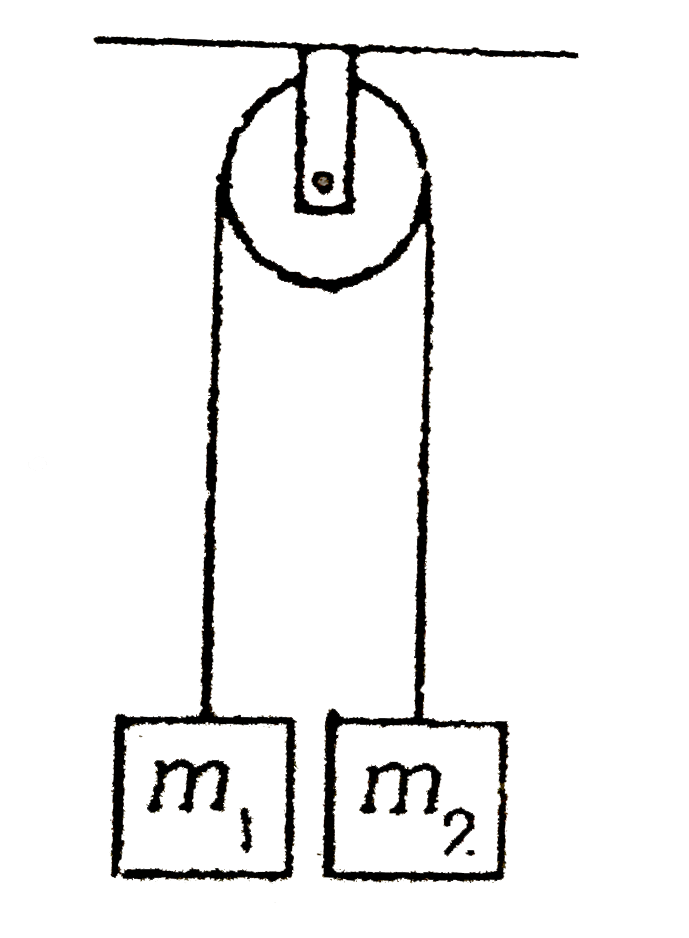
We know that accelarations a1 and a2 are given by the following equations.
a2=m2−m1m2+m1g⏐⏐
⏐↓ and a1=m2−m1m2+m1g↑⏐
⏐⏐
Making use of eq. , we can find acceleration ac of the mass center. We denote upward direction positive and downward direction negative signs respectively.
M→ac=Σ(mi¯ai)→ (m1+m2)ac=m1a1−m2a2
Substituting values of accelerations a1 and a2, we obtain aC=2m1m2−m21+m22m1+m22
To find tension T in the string supporting the pulley, we again use eq.(9)
Σ→Fi=M→ac→ T−m1g−m2g=(m1+m2)ac
Substituting expression obtained for ac, we have
T=4m1m2m1+m2g
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgIn the system shown in the figure, which the following is correct? (Pulleys and strings are of negligible mass)
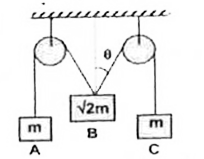 AThe system can never be in equilibriumBThe system remains in equilibrium at θ=45∘CIf the masses of A and C are changed then the equilibrium angle (if any) changesDIf all the masses are doubled, the equilibrium angle (if any) remains same.
AThe system can never be in equilibriumBThe system remains in equilibrium at θ=45∘CIf the masses of A and C are changed then the equilibrium angle (if any) changesDIf all the masses are doubled, the equilibrium angle (if any) remains same.
Consider the double Atwood’s machine as shown in the figure. What is acceleration of the masses ?
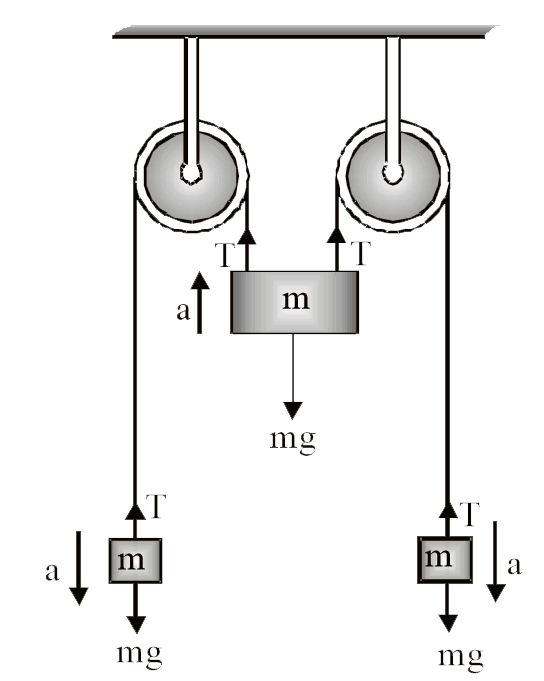
View SolutionConsider the double Atwood's machine as shown in the figure
(a) Whatis acceleration of the masses?
(b) What is the tension in each string?

View SolutionConsider the double Atwood's machine as shown in the figure
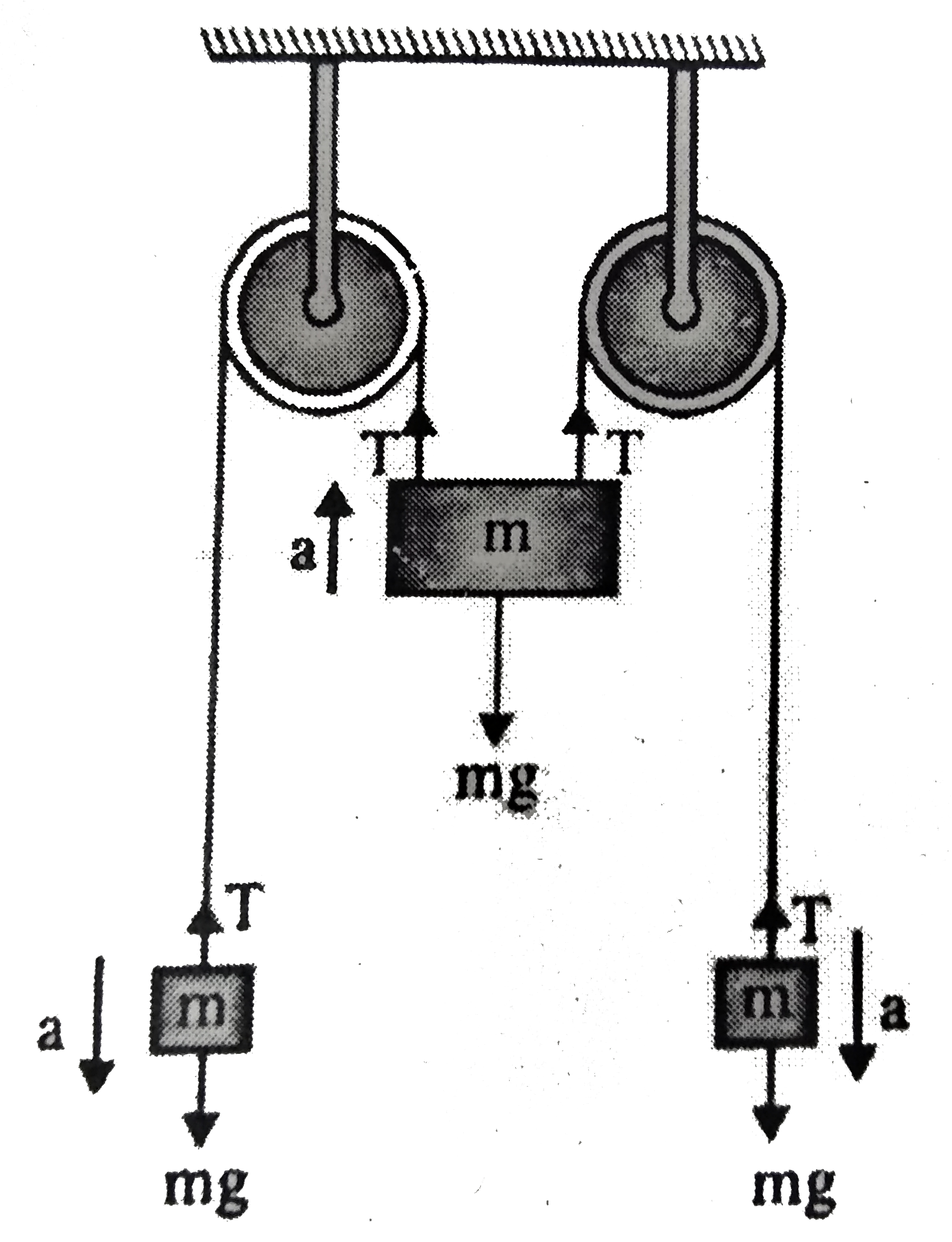
(a) What is acceleration of the masses?
(b) What is the tension in each string?
View SolutionThree masses m1,m2andm3 are attached to a string -pulley system as shown . All the three masses are held at rest and then released If m3 remains at rest , then

View SolutionIn the figure, the blocks have masses M1andM2(M1>M2) and acceleration a. The pulley P has a radius r and some mass the string not slip on the pulley
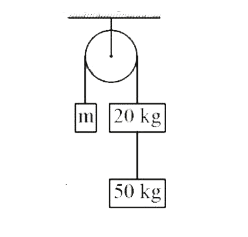
View SolutionFind the mass m in the figure for the system to be at rest
View Solution


