Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
$Σ m_{R} x_{R} = Σ m_{L} x_{L}, Σ m_{R} v_{R} = Σ m_{L} v_{L}$ and $Σ m_{R} a_{R} = Σ m_{L} a_{L}$
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass $m = 1 k g$ is placed over a wedge of mass $M = 4 k g$ as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Final velocity of the wedge is .......... $m / s$ :-

$\sqrt{3}$

$\sqrt{2}$

$\frac{1}{\sqrt{2}}$

$\frac{1}{\sqrt{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

By appplying conservation of momentum
$m v_{1} + M v_{2} = 0 \Rightarrow v_{1} = - 4 v_{2}$ …..(i)
By applying conservation of energy
$\frac{1}{2} m v_{1}^{2} + \frac{1}{2} M v_{2}^{2} = m g h \Rightarrow \frac{v_{1}^{2}}{2} + 2 v_{2}^{2} = 20$ ……(ii)
$v_{2} = \sqrt{2} m / s, v_{1} = 4 \sqrt{2} m / s$ .

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
$Σ m_{R} x_{R} = Σ m_{L} x_{L}, Σ m_{R} v_{R} = Σ m_{L} v_{L}$ and $Σ m_{R} a_{R} = Σ m_{L} a_{L}$
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass $m = 1 k g$ is placed over a wedge of mass $M = 4 k g$ as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

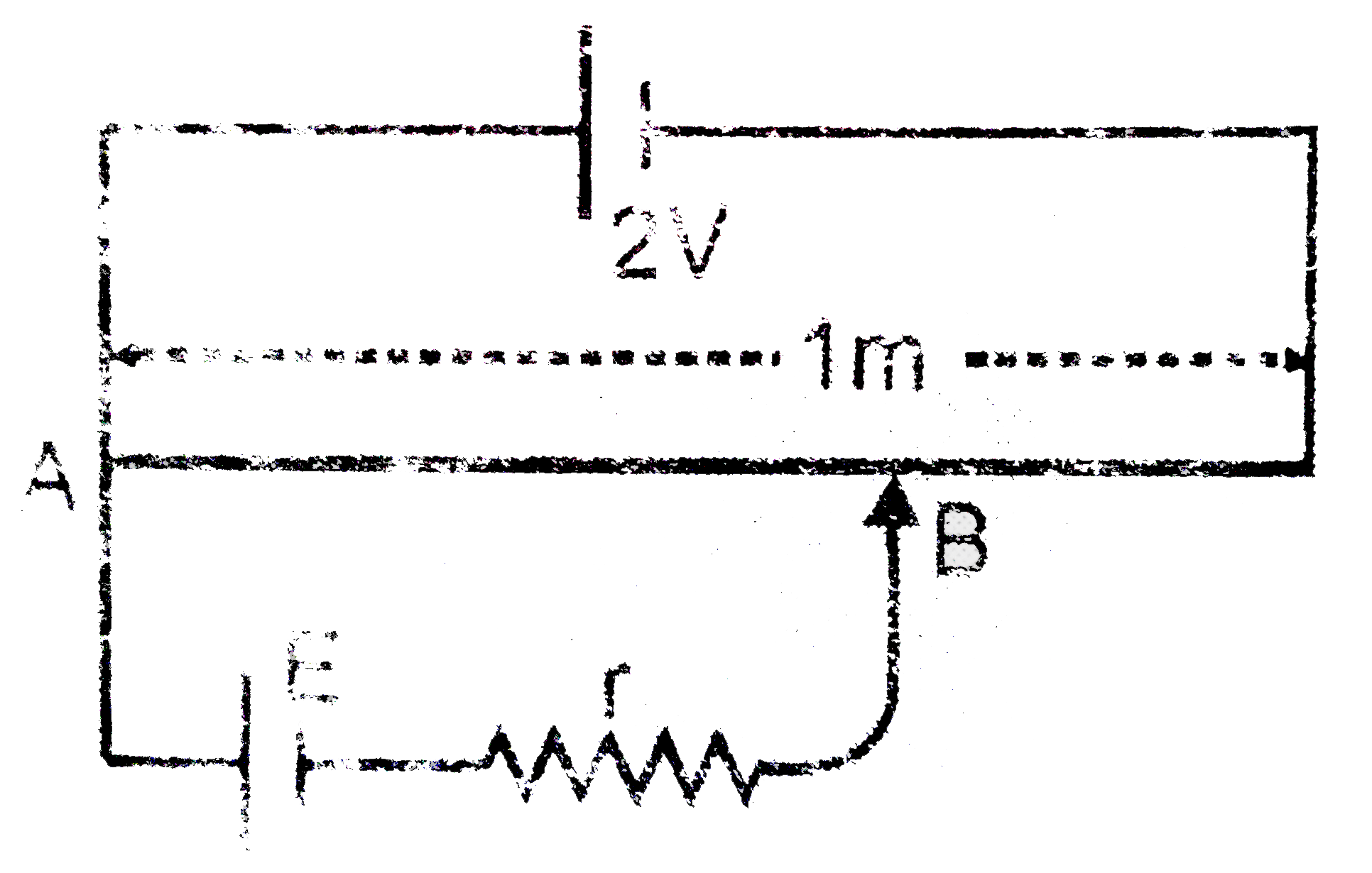
The block will strike the x-axis at $x =$ ............ $m$ :-
A $4.2$
B $7.6$
C $5.6$
D $6.8$
Question 2 - Select One
Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
$Σ m_{R} x_{R} = Σ m_{L} x_{L}, Σ m_{R} v_{R} = Σ m_{L} v_{L}$ and $Σ m_{R} a_{R} = Σ m_{L} a_{L}$
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass $m = 1 k g$ is placed over a wedge of mass $M = 4 k g$ as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

At the same instant reaction on the wedge from the ground is ........N.
A $42.5$
B $40$
C $43.46$
DNone of these
Question 3 - Select One
Comprehension # 1
If net force on a system in a particular direction is zero (say in horizontal direction) we can apply:
$Σ m_{R} x_{R} = Σ m_{L} x_{L}, Σ m_{R} v_{R} = Σ m_{L} v_{L}$ and $Σ m_{R} a_{R} = Σ m_{L} a_{L}$
Here R stands for the masses which are moving towards right and L for the masses towards left, x is displacement, v is veloctiy and a the acceleration (all with respect to ground). A small block of mass $m = 1 k g$ is placed over a wedge of mass $M = 4 k g$ as shown in figure. Mass m is released from rest. All surface are smooth. Origin O is as shown.

Normal reaction between the two blocks at an instant when absolute acceleration of $m$ is $5 \sqrt{3} m / s^{2}$ at $60^{\circ}$ with horizontal is ......... N. Normal reaction at this instant is making $30^{\circ}$ with horizontal :-
A6
B10
C4
D5