Determine the centre of gravity of a thin homogeneous plate having the form of a rectangle with sildes r and from which a semicircle with a radius r is cut out of figure.

The correct Answer is:
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B14videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle travels along a semicircle of radius R in 2 s. The velocity of the particle is
AπRBRC2πRD2R - Question 2 - Select One
A particle travels along a semicircle of radius R in 2 s. The velocity of the particle is
AπRBRC2πRD2R
Find the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionDetermine the position of the centre of mass of a hemisphere of radius R.
View SolutionFind the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1andR2.
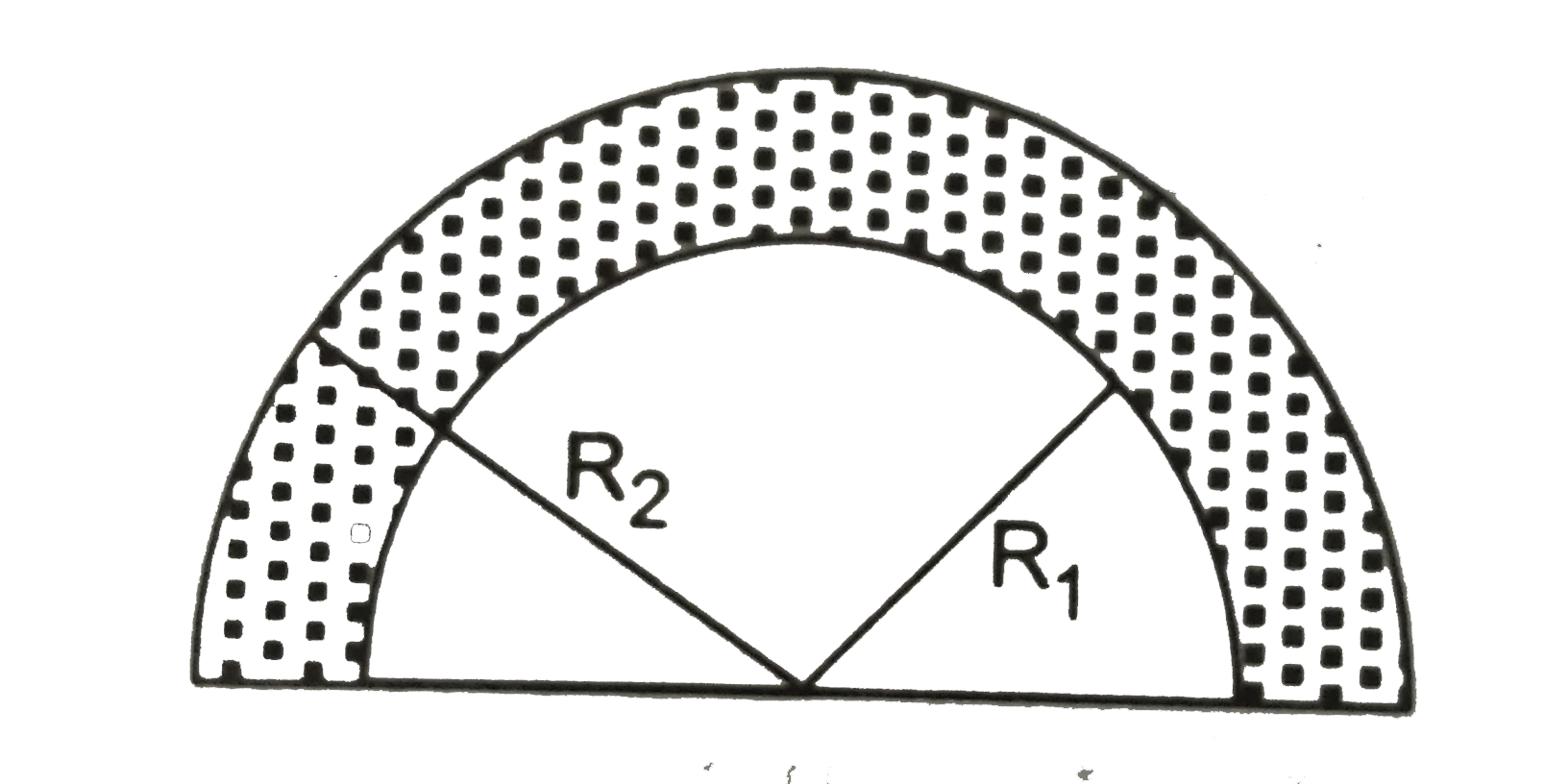 View Solution
View SolutionRectangles are inscribed inside a semicircle of radius r. Find the rectangle with maximum area.
View SolutionFind x and y coordinats of the centre of mass of the plate shown in figure from which a square of side 2 m is cut out.
 View Solution
View SolutionA thin homogeneous lamina is in the form of a circular disc of radius R. From it a circular hole exactly hall the radius of the lamina and touching the lamina's circumference is cut off. Find the centre of mass of the remaining part.
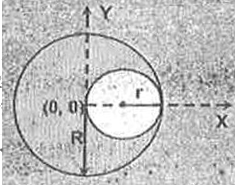 View Solution
View Solution

