A simple pendalum is suspended from a peg on a verticle wall . The pendulum is pulled away from the well is a horizental position (see fig) and released . The bell his the well the coefficient of resitution being 2√5
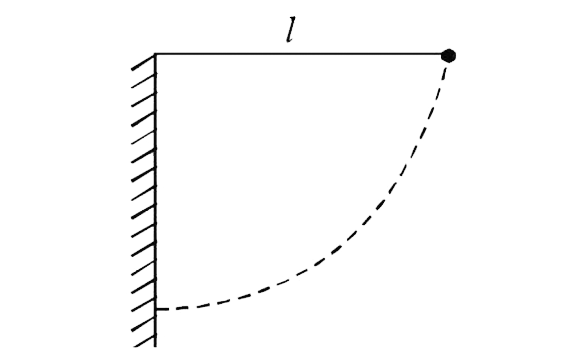
what is the miximum number of colision after which the amplitube of secillections between less that 60 digree ?
The correct Answer is:4

After 1st collision
−2√5√2gl=√2gl(1−cosθ)
cosθ15
Fro IInd collision
2√5.2√5√2gl=√2gl(1−cosθ)
For nth collision
(2√5)n=√1−cosθ⇒(45)n=1−cosθ
cosθ=1−(45)n
Put n=0,1,2,3 and get answer
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B14videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
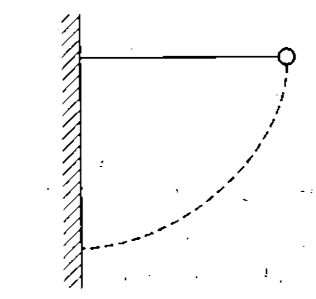
A simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
 View Solution
View SolutionA simple pendulum is suspended from a peg on a wall which is inclined at an angle of 30∘ with the vertical. The pendulum is pulled away from the wall to a horizontal position (with string just taut) and released. The bob repeatedly bounces off the wall, the coefficient of restitution being e=2√5
Find the number of collisions of the bob with the wall, after which the amplitude of oscillation (meaured from the wall) becomes less than 30∘
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is 2√5. After how many collisions the amplitude of vibration will becomes less then 60∘.
A6B3C5D4 - Question 2 - Select One
A simple pendulum is hanging from a peg inserted in a vertical wall. Its bob is stretched in horizontal position from the wall and is left free to move. The bob hits on the wall the coefficient of restitution After how many collsions the amplitude of vibration will become less than 60∘
A6B3C5D4 - Question 3 - Select One
A circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If a clown holds on to hoop instead of passing through it, what is the position of the cable so that he doesn't hit his head on the ceiling as he swings upward?A2v20gBv20gCv202gDv204g
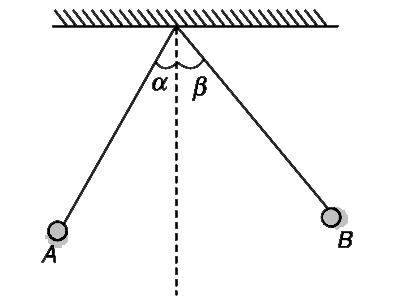
Two identical simple pendulums A and B are fixed at same point. They are displaced by very small angles α and β(=2α) respectively and are simultaneously released from rest at time t = 0. Collisions between the pendulum bobs are elastic and length of each pendulum is l.
(a) What is the minimum number of collisions between the bobs after which the pendulum B will again reach its original position from where it was released ?
(b) Find the time (t) at which B reaches its initial position for the first time after the release.
(c) Write the kinetic energy of pendulum B just after nth collision? Take mass of each bob to be m.
 View Solution
View SolutionAfter receiving the lamp, Aladdin and Abu are on their way to get out from the cave when they found a statue of Sir Hussain, one of the most powerful Royal General to walk on Earth. Below the statue is written a real life problem that Sir Hussain solved and in order to get out of the cave one must solve this riddle. Aladdin out of options starts reading the riddle- Once upon a time in the Kingdom far far away lived Sir Hussain, the chief Royal General. He was very proud of his men and he liked to invite the King to come and watch drill exer- cises which demonstrated the fighting techniques and tactics of the squad he was in charge of. But time went by and one-day Sir Hussain had a major argument with an old witch (there were rumours that the argument occurred after the general spoke badly of the witch flying techniques. That seemed to hurt the old witch very deeply). As the result of the argument, the witch put a rather strange curse upon the general. It sounded all complicated and quite harmless: "If the squared distance between some two soldiers equals to 5, then those soldiers will conflict with each other!" The drill exercises are held on a rectangular n × m field, split into nm square 1 × 1 segments for each soldier. Thus, the square of the distance between the soldiers that stand on squares (x1,y1) and (x1,y2) equals exactly(x1−x2)2+(y1−y2)2. Now not all nm squad soldiers can partici- pate in the drill exercises as it was before the old witch curse. Unless, of course, the general wants the soldiers to fight with each other or even worse. For example, if he puts a soldier in the square (2, 2), then he cannot put soldiers in the squares (1, 4), (3, 4), (4, 1) and (4, 3) — each of them will conflict with the soldier in the square (2, 2).
Find the sum of maximum number of soldiers that can be simultaneously positioned on this field for each of the following cases
i) 1002 2
ii) 451 2
iii) 780 2
iv) 121 2View SolutionAfter receiving the lamp, Aladdin and Abu are on their way to get out from the cave when they found a statue of Sir Hussain, one of the most powerful Royal General to walk on Earth. Below the statue is written a real life problem that Sir Hussain solved and in order to get out of the cave one must solve this riddle. Aladdin out of options starts reading the riddle- Once upon a time in the Kingdom far far away lived Sir Hussain, the chief Royal General. He was very proud of his men and he liked to invite the King to come and watch drill exer- cises which demonstrated the fighting techniques and tactics of the squad he was in charge of. But time went by and one-day Sir Hussain had a major argument with an old witch (there were rumours that the argument occurred after the general spoke badly of the witch flying techniques. That seemed to hurt the old witch very deeply). As the result of the argument, the witch put a rather strange curse upon the general. It sounded all complicated and quite harmless: "If the squared distance between some two soldiers equals to 5, then those soldiers will conflict with each other!" The drill exercises are held on a rectangular n × m field, split into nm square 1 × 1 segments for each soldier. Thus, the square of the distance between the soldiers that stand on squares (x1,y1) and (x1,y2) equals exactly(x1−x2)2+(y1−y2)2. Now not all nm squad soldiers can partici- pate in the drill exercises as it was before the old witch curse. Unless, of course, the general wants the soldiers to fight with each other or even worse. For example, if he puts a soldier in the square (2, 2), then he cannot put soldiers in the squares (1, 4), (3, 4), (4, 1) and (4, 3) — each of them will conflict with the soldier in the square (2, 2).
Find the sum of maximum number of soldiers that can be simultaneously positioned on this field for each of the following cases
i) 53×81
II) 2×103
III) 1×104View SolutionA 4.00kg block carrying a charge Q=50.0μC is connected to a spring for which k = 100 N/ m. The block lies on a frictionless horizontal track, and the system is immersed in a uniform electric field of magnitude E=5.00×105Vm, directed as shown in figure. If the block is released from rest when the spring is unstretched (at x = 0).

(a) By what maximum amount does the spring expand?
(b) What is the equilibrium position of the block?
(c) Show that the block's motion is simple harmonic and determine its period.
(d) Repeat part (a) if the coefficient of kinetic friction between block and surface is 0.2.View SolutionIn the following paragraph read the passage completely to answer the questions from the given options.
"A principal fruit of friendship", Francis Bacon wrote in his timeless meditation on the subject, "is the ease and discharge of the fullness and swellings of the heart, which passions of all kinds do cause and induce." For Thoreau, friendship was one of life's great rewards. But in today's cultural landscape of muddled relationships scattered across -various platforms for connecting, amidst constant debates about whether our Facebook 'friendships are making us more or less happy, it pays to consider what friendship actually is. That's precisely what CUNY Philosophy professor Massimo Pigliucci explores in Answers for Aristotle : How Science and Philosophy Can Lead Us to a More Meaningful Life (public library), which also gave us this provocative read on the science of what? we call “intuition'.
Philosophers and cognitive scientists agree that, friendship is an essential ingredient of human happiness. But beyond the dry academic definitions like, says voluntary interdependence between two persons over, time, which is intended to facilitate socio-emotional goals of the participants, and may involve varying types and degrees of companionship, intimacy, affection and mutual assistance”—lies a body of compelling research that sheds light on how, precisely, friendship augments happiness. The way friendship enhances well-being, it turns out his nothing to do with quantity and everything to do with quality researchers confirm that itisn't the number of friends (ot, in the case of Facebook, 'friends). Wall
The change in the present situation which has forced us to rethink the concept of friendship isView Solution

