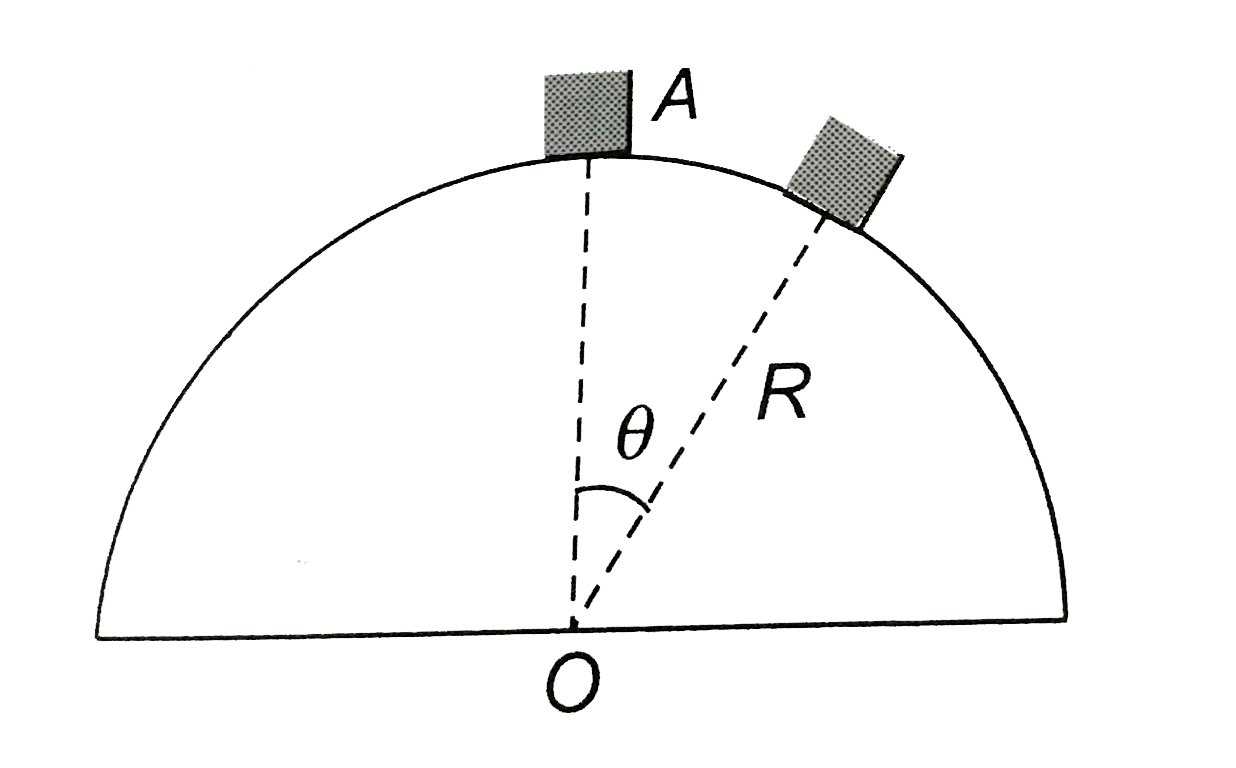
A hemisphere of radius R and mass 4 m is free to slide with its base on a smooth horizontal table . A particle of mass m is placed on the top of the hemisphere . The angular velocity of the particle relative to centre of hemisphere at an angular displacement θ when velocity of hemisphere has become v is
The correct Answer is:5vRcosθ
Let v= velocity of wege and u= velocity of particle relative to wedge
COLM
⇒m(v+ucosθ)+4mv=0
⇒ucosθ=−5v,ω=uR=5vRcosθ
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B14videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A hemisphere of radius R and of mass 4m is free to Slide with its base on a smooth horizontal table. A particle mass m is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement θ when velocity of hemisphere has become v.
 View Solution
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if v<√gRBit will start moving along a circular path if v>√gRCit will start moving along a parabolic path if v<√gRDit will start moving along a parabolic path if v>√gR - Question 2 - Select One
A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is
 Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ)
Amg(3−2cosθ)Bmg(3cosθ−2)Cmg(4cosθ−3)Dmg(4−3cosθ) - Question 3 - Select One

A uniform solid hemisphere of radius 10 m and mass 64 kg is placed with its curved surface on the smooth horizontal surface and a string AB of length 4 m is attached to point A on its rim as shown in the figure Find the tension in the string if hemisphere is in equilibrium.A320 NB640 NC180 ND360 N
A particle of mass m slides down from the vertex of semi- hemisphere, without any initial velocity. At what height from horizontal will the particle leave the sphere-
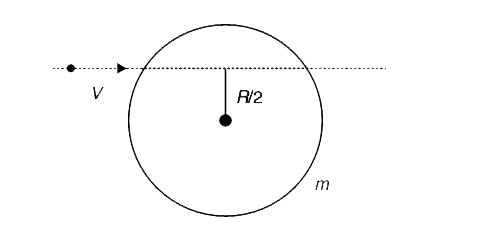
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
 View Solution
View SolutionA particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
View SolutionA partcle rests on the top of a hemisphere of radiu R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down it-
View SolutionA partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
View Solution

