Block A of mass m/2 is connected to one end of light rope which passes over a pulley as shown in fig. A man of mass m climbs the other end of rope with a relative acceleration of g/6 with respect to rope. Find the acceleration of block A and tension in the rope.

The correct Answer is:4g9,13mg18
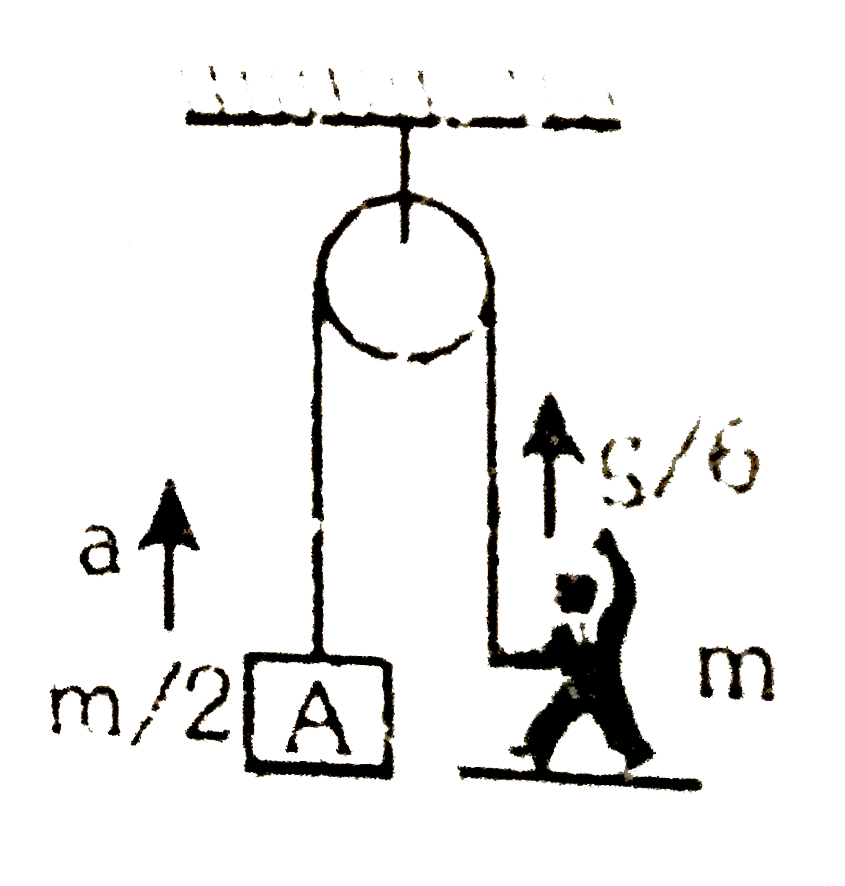
mg−T=m(a−g6) …(i)
⇒T−m2g=m2a …(ii)
For solving eq. (i) & (ii)
a=4g9 & T=1318mg
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B14videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A boy of mass 40kg climbs up a rope with an acceleration of 1.2ms−2.What is the tension in the rope?
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In order to raise a mass of 100kg a man of mass 60kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is: Take g=10m/s2
A1432NB928NC1218ND642N - Question 2 - Select One
A man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?
 A(M+m)g2B(M+m)gC(M−m)gD(M+2m)g
A(M+m)g2B(M+m)gC(M−m)gD(M+2m)g - Question 3 - Select One
As shown in figure a monkey of 20g mass is holding a light rope that passes over a frictionless pulley. A bunch of bananas of the same mass is tied to the other end of rope. Inorder to get access to the bunch the monkey starts climbing the rope. The distance between the monkey and the bananas is
 ADecreasingBIncreasingCUnchangedDNothing can be stated
ADecreasingBIncreasingCUnchangedDNothing can be stated
To raise a weight which is half as much again as his weight a man fastens a rope to it and passes over a smooth pulley, he then climbs up the rope with an acceleration 6g7 relative to the rope. Show that the weight rises with acceleration 87, and find the tension of the rope.
View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
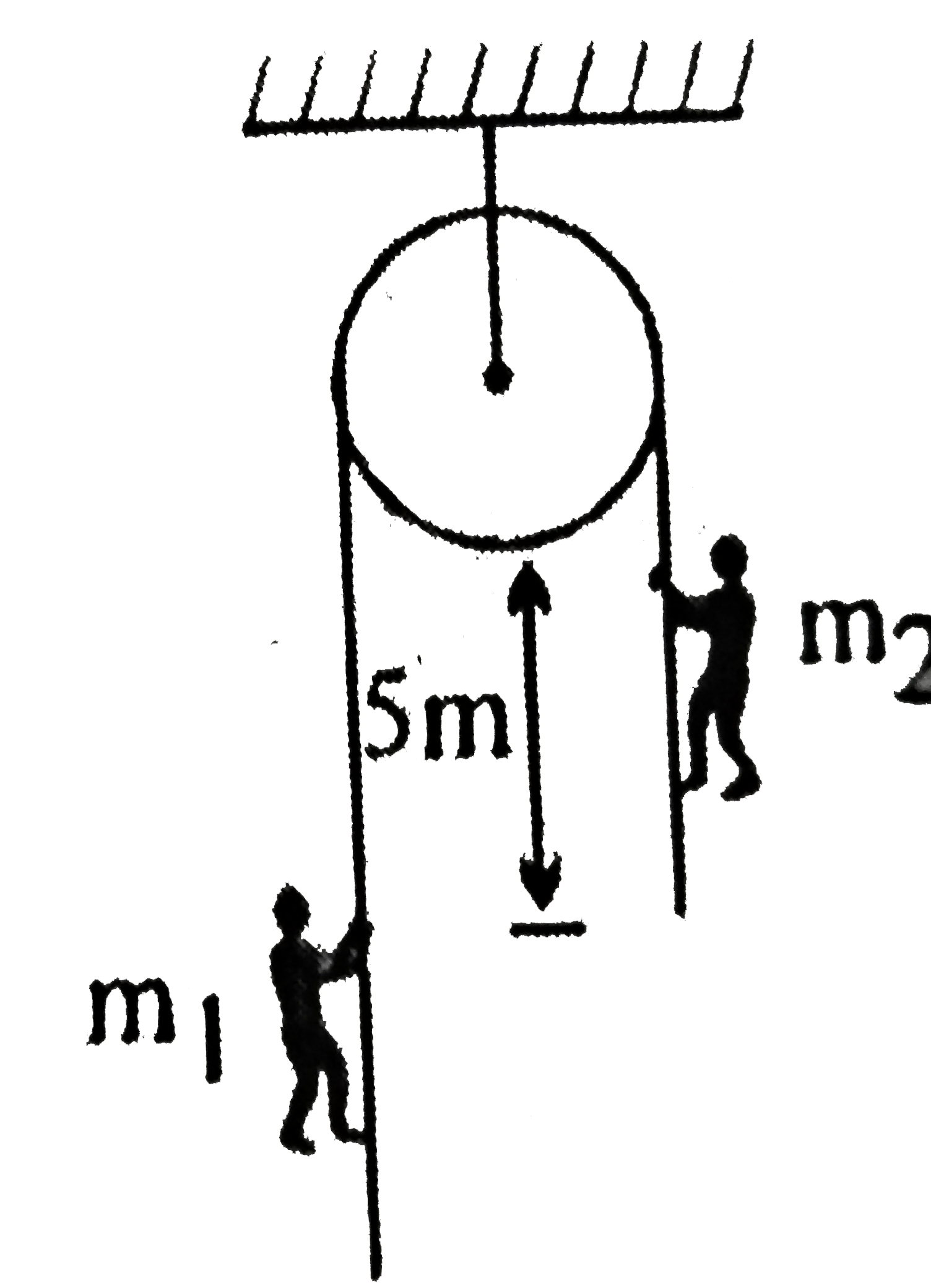 View Solution
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . A force P is applied to the other end of the rope . (a) Find the acceleration of the block and the rope . (b) Find the force that the rope exerts on the block M in terms of P, M and m .
View SolutionIf a monkey moves upward with respect to the rope with acceleration g/2 then acceleration of block, if masses of block and monkey are same
 View Solution
View SolutionA monkey of mass m climbs up to a rope hung over a fixed pulley. The opposite end of the rope is tied to a weight of mass M lying on a horizontal plane. Neglecting the friction, find the acceleration of both the bodies (relative to the plane) and the tension of the rope for the three cases:
(i) The monkey does not move with respect to the rope
(ii) The monkey moves upwards with respect to the rope with acceleration a.
(iii) The monkey moves downwards with respect to the rope, with acceleration a.View Solution

