Rectangle ABCD is inscribed in a circle. If the radius of the circle is 2 and , what is the area of the shaded region ?

A
B
C
D
Video Solution
Text Solution
The correct Answer is:A
As usual, the key here is to add to the figure. And here, as is so often the case with circles, you should add radii. The equilateral triangles formed by and the radii, and by and the radii, have central angles of
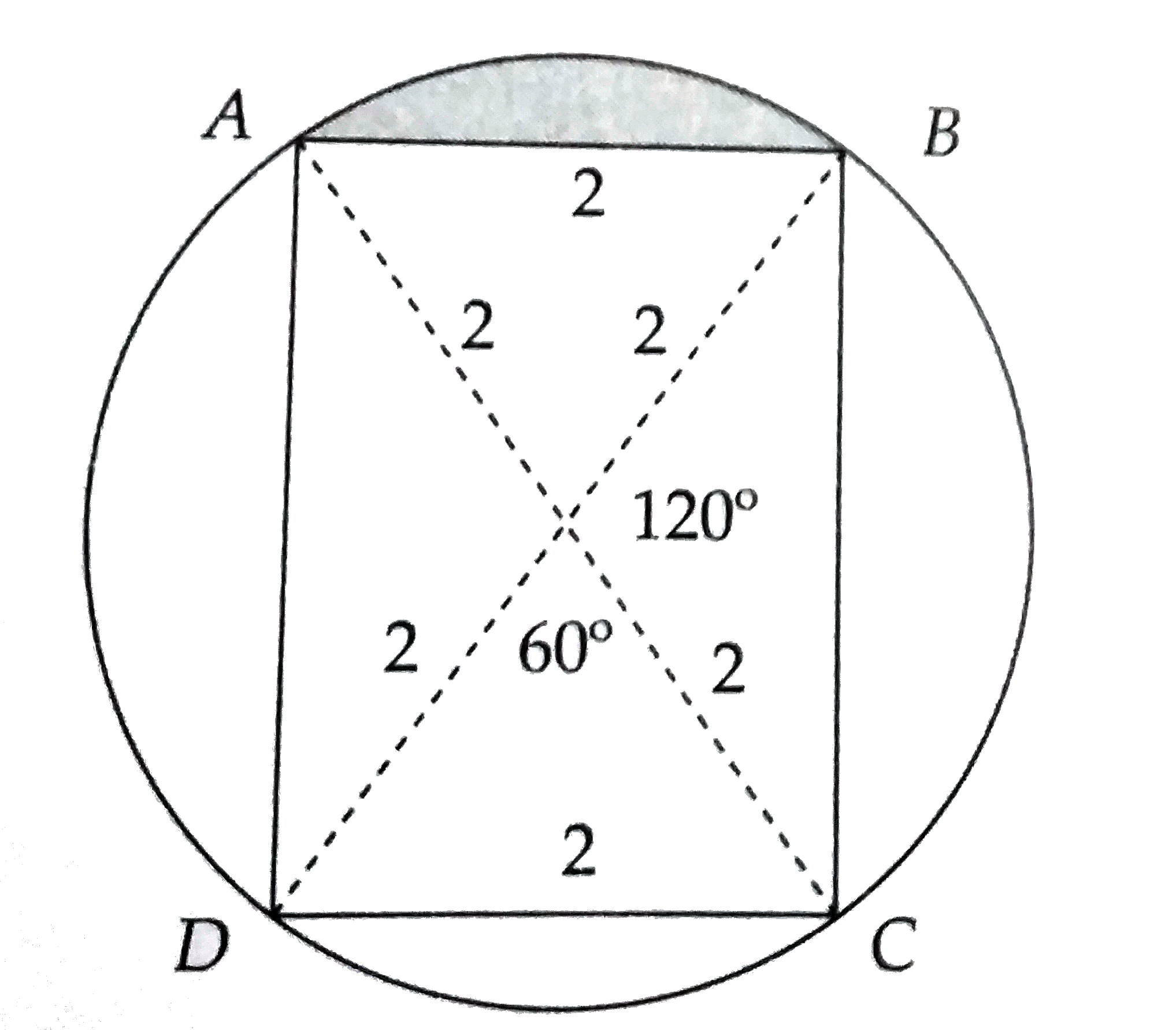
The shaded region is what's left of the sector after you subtract the area of an equilateral triangle. To find the area of the shaded region, find the areas of the sector and triangle, then substract the latter from the former. The sector is exactly one - sixth of the circle (because is one - sixth of ). Thus,
Area of the sector
Use the formula for the area of an equilateral triangle to close in on the answer.
Area of an equilateral triangle
The shaded area, then, is .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - PLANE GEOMETRY EXERCISE - PLANE GEOMETRY FOLLOW - UP TEST6videos
PLANE GEOMETRY
- BOOK - KAPLANCHAPTER - MISCELLANEOUS TOPICS EXERCISE - MISCELLANEOUS TOPICS FOLLOW - UP TEST12videos
MISCELLANEOUS TOPICS
- BOOK - KAPLANCHAPTER - PRACTICE TEST 1 EXERCISE - PRACTICE TEST50videos
PRACTICE TEST 1
Similar Questions
Knowledge Check
- Question 1 - Select One

If the circumference of the circle above is 16π, what is the total area of the shaded regions?A64πB32πC12πD8π - Question 2 - Select One
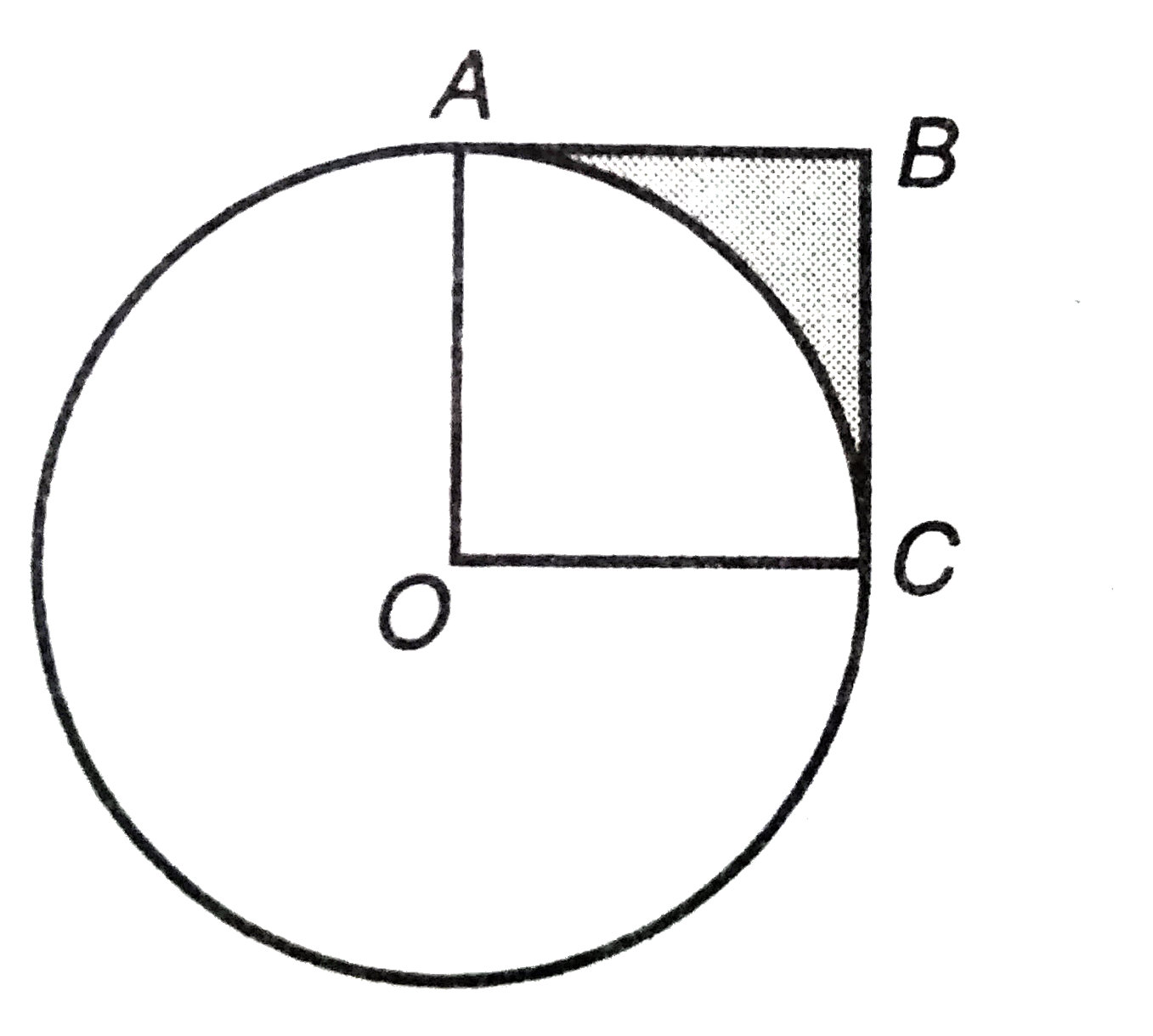
In the figure above, OABC is a square. If the area of circle O is 2π, what is the area of the shaded region?Aπ2−1B2−π2Cπ−2Dπ−12 - Question 3 - Select One
In the diagram to the right , the circle with center O is inscribed in equilateral triangle BCD. If the radius of the circle is 4, what is the ratio of the perimeter of △BCD to the area of △BCD ?
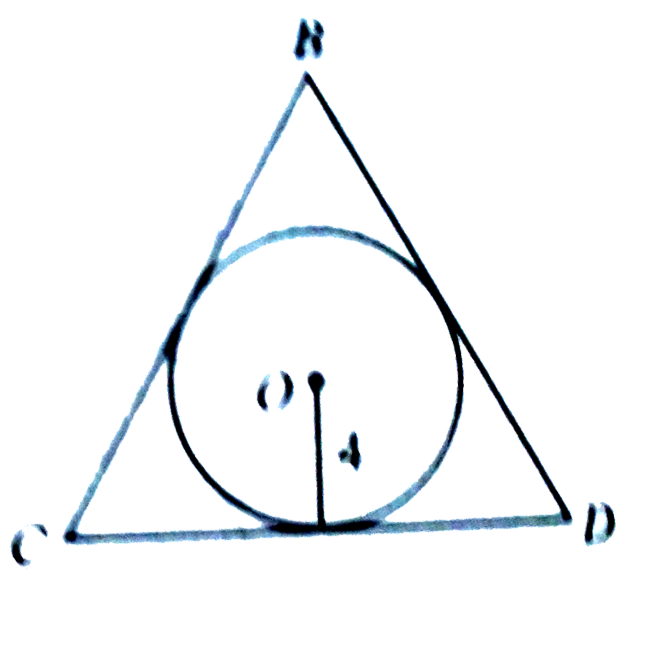 A1:2√3B1:√3C1:2D1:4
A1:2√3B1:√3C1:2D1:4
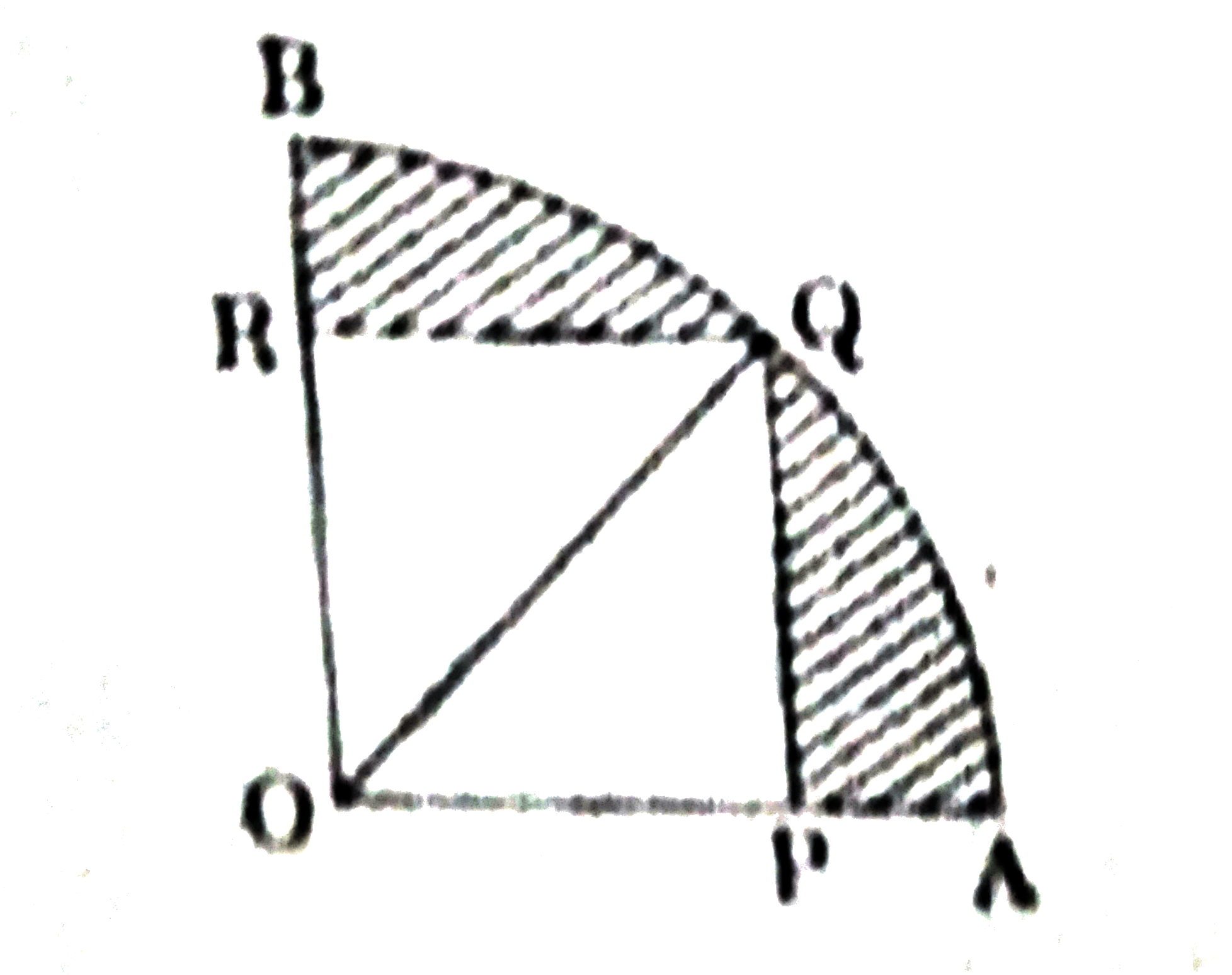
In Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View SolutionBE and CD are both diameters of circle with centre A (see figure). If the area of the circle is 180units2, what is the total area of the shaded regions?
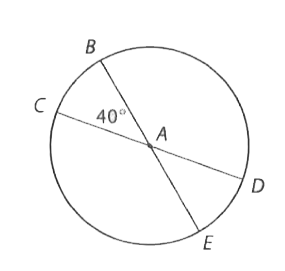 View Solution
View SolutionThe given figure shows a rectangle ABCD inscribed in a circle as shown alongside.
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.
 View Solution
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View SolutionIn the figure, ABCD is a rectangle. What is the area of the shaded region in the figure?
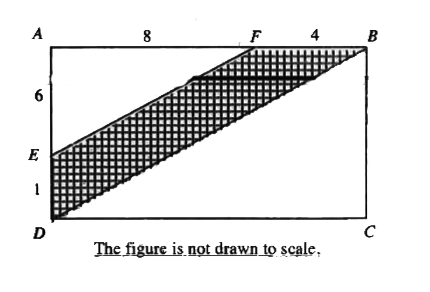 View Solution
View Solution