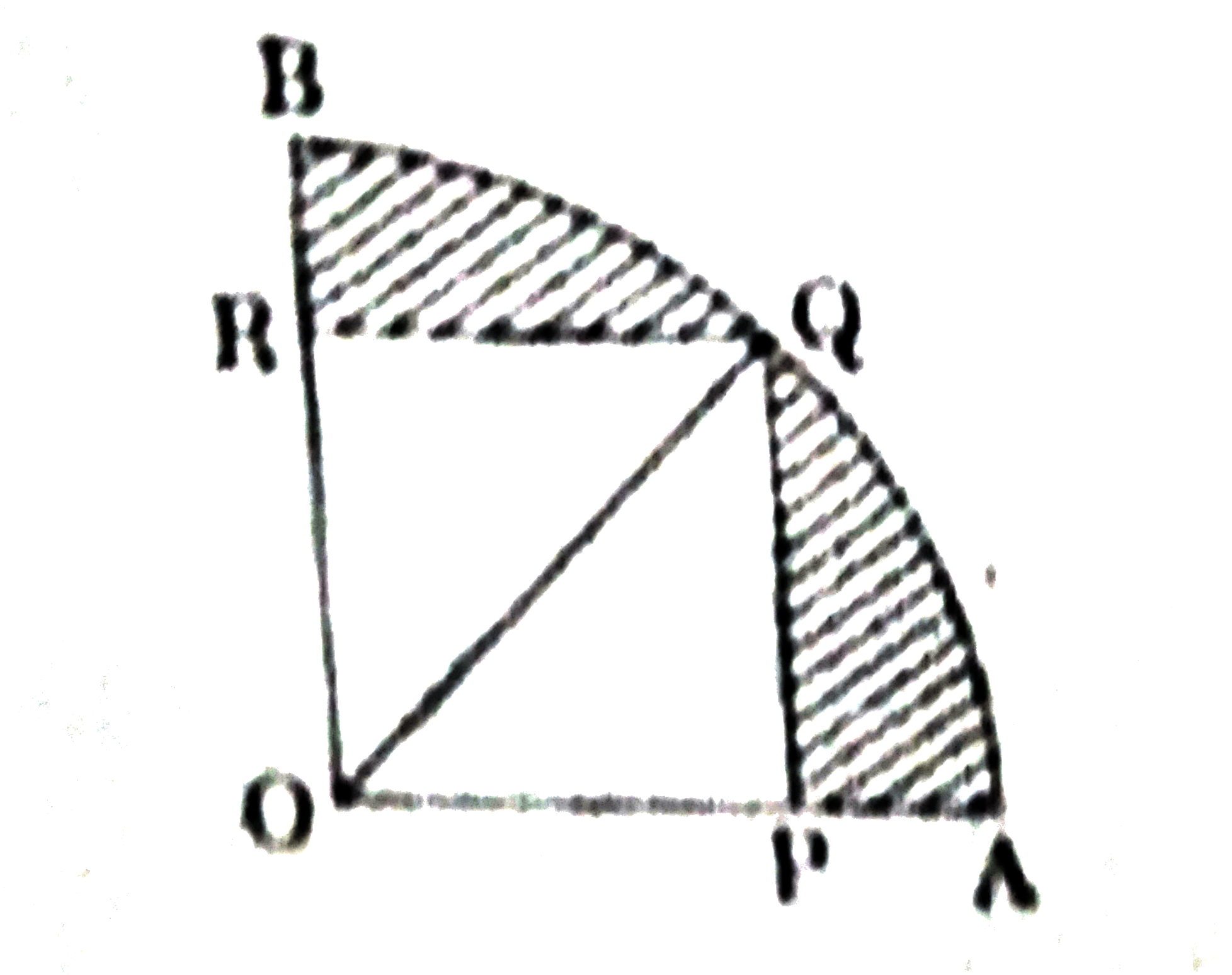
In Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
To find the area of the shaded region in the given problem, we will follow these steps:
Step 1: Identify the given values
We are given the radius of the circle, which is r=6√2 cm.
Step 2: Determine the side length of the square
The diagonal of the square OPQR is equal to the radius of the circle OQ. Since the square is inscribed in a quadrant, we can use the Pythagorean theorem in triangle OQP:
OQ2=OP2+PQ2
Let the side length of the square be a. Then OP=PQ=a. Therefore, we have:
(6√2)2=a2+a2
Calculating (6√2)2:
72=2a2
Dividing both sides by 2:
a2=36
Taking the square root:
a=6 cm
Step 3: Calculate the area of the quadrant
The area of a quadrant is given by the formula:
Area of quadrant=θ360×πr2
For a quadrant, θ=90∘:
Area of quadrant=90360×π(6√2)2
Calculating (6√2)2:
(6√2)2=72
Now substituting this into the area formula:
Area of quadrant=14×π×72=18π cm2
Using π≈227:
Area of quadrant≈18×227=3967≈56.57 cm2
Step 4: Calculate the area of the square
The area of the square OPQR is:
Area of square=a2=62=36 cm2
Step 5: Find the area of the shaded region
The area of the shaded region is the area of the quadrant minus the area of the square:
Area of shaded region=Area of quadrant−Area of square
Substituting the values we found:
Area of shaded region=56.57−36=20.57 cm2
Final Answer:
The area of the shaded region is approximately 20.57 cm2.
---
We are given the radius of the circle, which is r=6√2 cm.
The diagonal of the square OPQR is equal to the radius of the circle OQ. Since the square is inscribed in a quadrant, we can use the Pythagorean theorem in triangle OQP:
The area of a quadrant is given by the formula:
The area of the square OPQR is:
The area of the shaded region is the area of the quadrant minus the area of the square:
The area of the shaded region is approximately 20.57 cm2.
Similar Questions
Knowledge Check
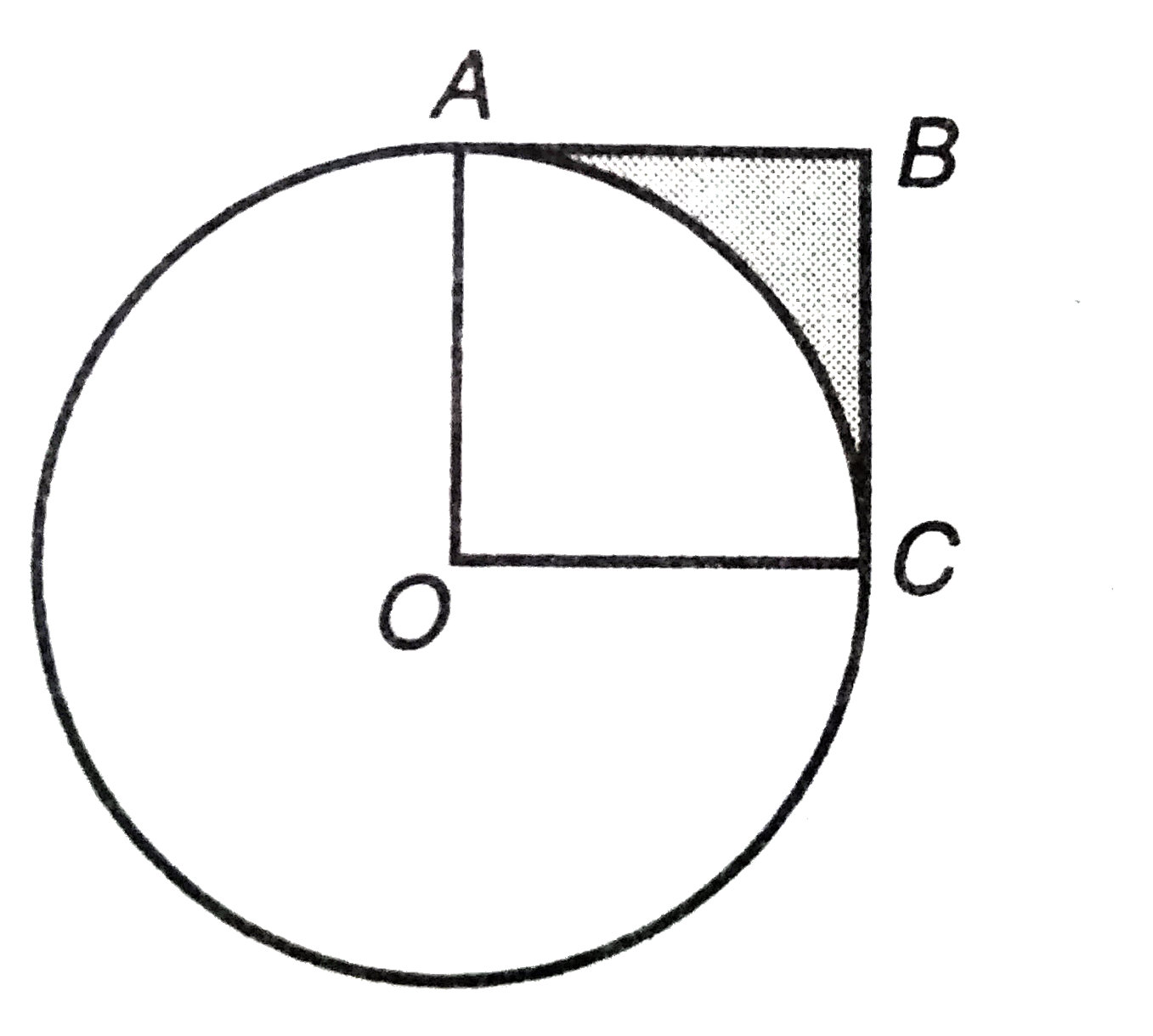
In the figure above, OABC is a square. If the area of circle O is 2π, what is the area of the shaded region?Aπ2−1B2−π2Cπ−2Dπ−12
In Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Figure, OCDE is a rectangle inscribed in a quadrant of a circle of radius 10cm. If OE=2√5cm , find the area of the rectangle.
View SolutionIn the given figure, ABCD is a square of side 7 cm. DPBA and DQBC are quardrants of circles each of the radius 7 cm. Find the area of the shaded region.

View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
View SolutionFind the area of a quadrant of a circle whose radius is 14 cm.
View Solution