Question

When a right triangle of area 4 is rotated ${360}^{\circ }$ about its longer leg, the solid that results has a volume of 16. What is the volume of the soild that results when the same right triangle is rotated about its shorter leg ?

Options

A. `4.39`
B. `8.77`
C. `16.93`
D. `35.09`

Answer

D

Explanation

When you write the equations for the volumes, try to pluge in the area of the triangle, since that is known. When you rotate a right triangle about a leg, you get a cone :

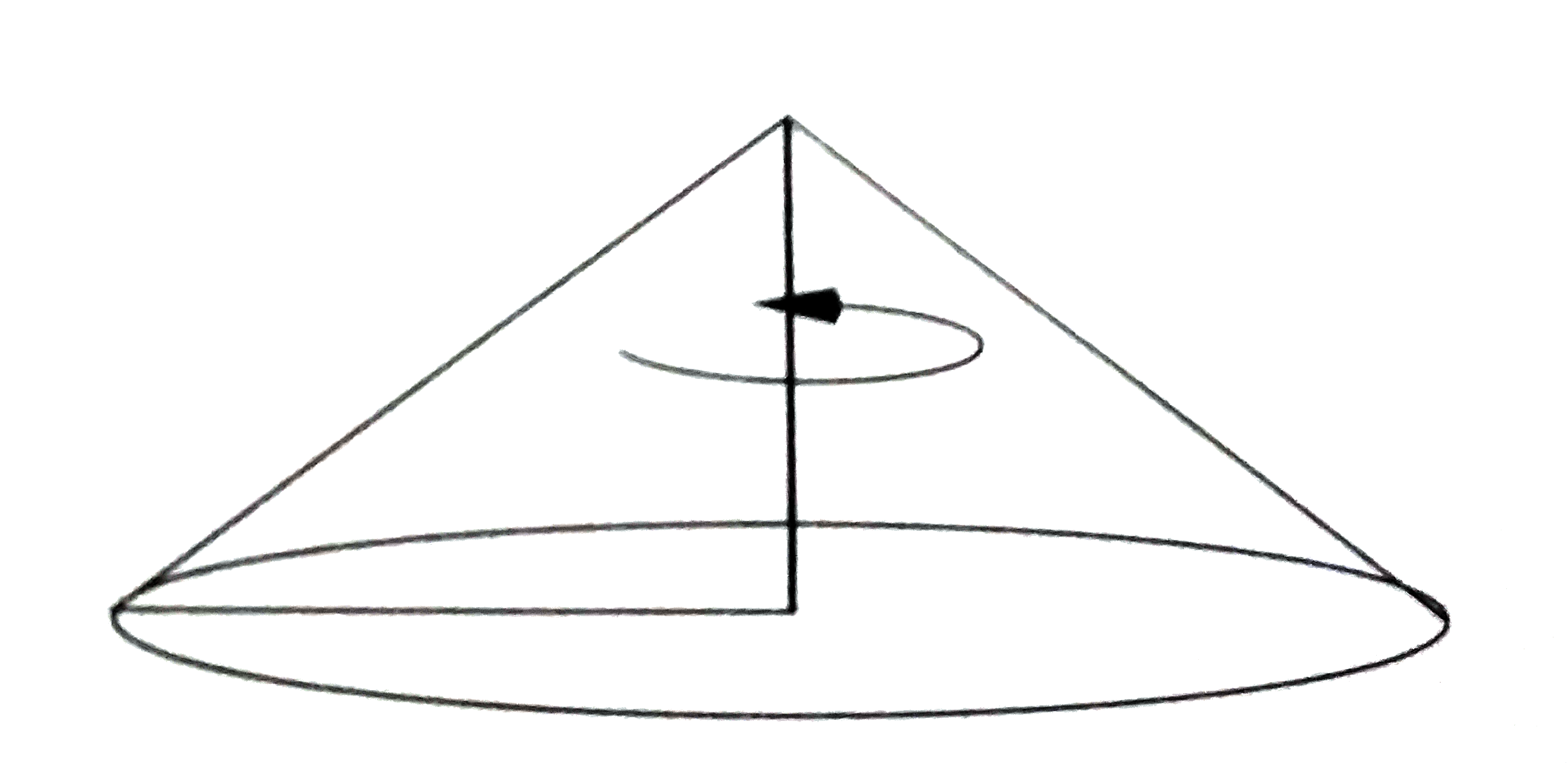
One leg becomes the base radius, and the other becomes the height of the cone. Call the short leg a and the long leg b and plug them into the cone volume formula :
Volume of Cone `=(1)/(3)pi r^(2)h=(1)/(3)pi a^(2)b`
It's also given that the area of the right triangle is 4. Therefore,
Area of Right Triangle `=(1)/(2)(ab)=4`
Plug ab = 8 into the expression for the volume of the cone and you can solve for a :
`(1)/(3)pi a^(2)b=16`
`(1)/(3)pi a (ab)=16`
`(1)/(3)pi a(8)=16`
`(8pi)/(3)a = 16`
`a=16((3)/(8pi))=(6)/(pi)`
Then you can plug `a = (6)/(pi)` into the equation ab = 8 to solve for b :
ab = 8
`((6)/(pi))b = 8`
`b=8((pi)/(6))=(4pi)/(3)`
When the triangle is rotated about its shorter leg, a becomes the height and b becomes the base radius. Thus,
Volume `= (1)/(3)pi r^(2)h = (1)/(3)pi b^(2)a = (pi)/(3)b(ab)`
`=((pi)/(3))((4pi)/(3))(8)=(32pi^(2))/(9)~~35.09`