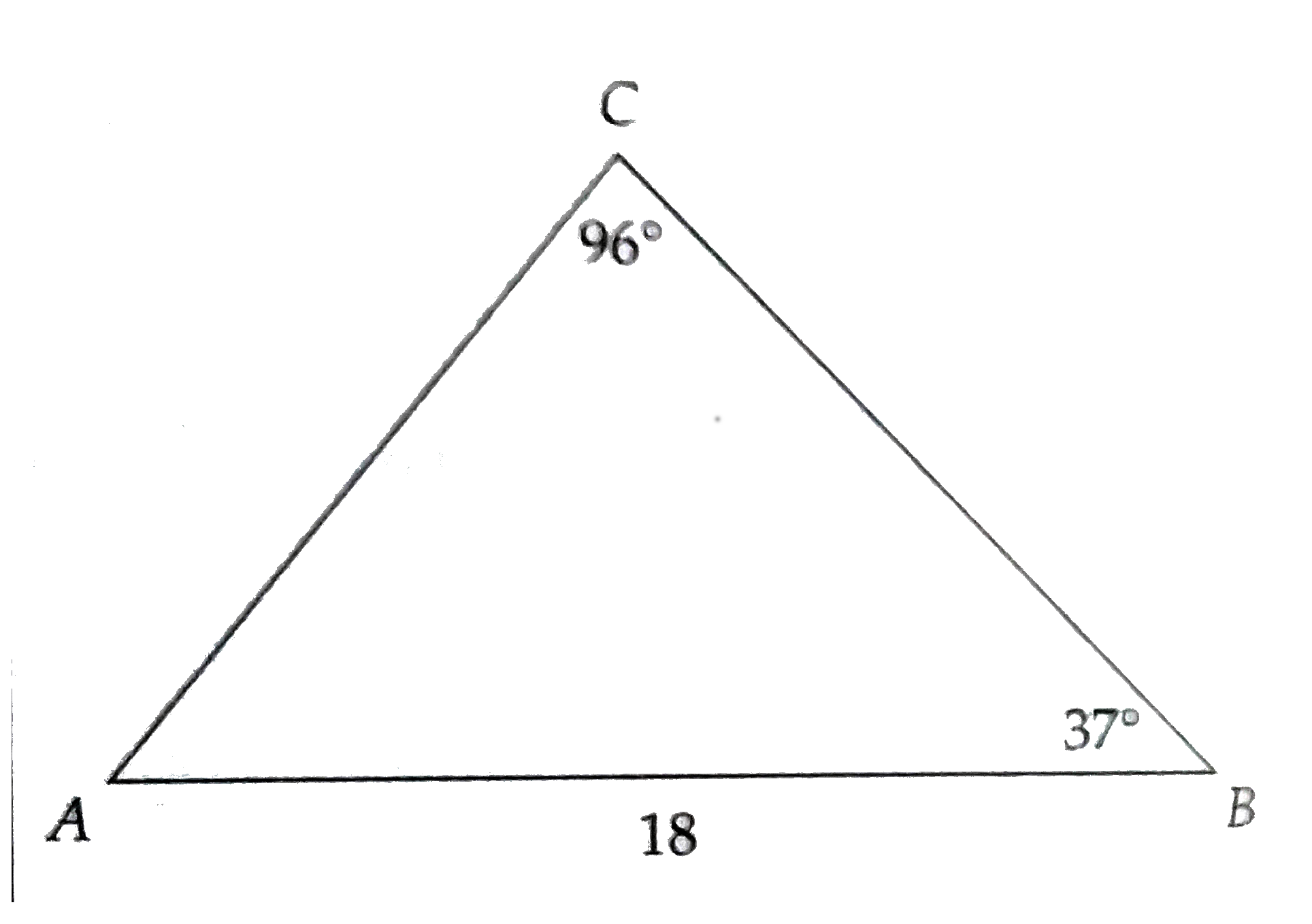
What is the length of side BC in Figure ?
A
7.3
B
7.7
C
8.1
D
8.5
Video Solution
Text Solution
The correct Answer is:D
You might not think that this is a trigonometry question at first. There's no ''sin,'' ''cos,'', or any other explicit tring function mentioned in the stem. And the triangle's not a right triangle. But trig is the tool you have to use answer this question. This is a case of ''solving a triangle'', that is, finding the length of one or more sides.
With the Law of Sines and the Law of Cosines and a calculator, you can solve almost any triangle. If you know any two angles - which of course means that you know all three - and one side, you can use the Law of Since to find the other two sides. If you know two sides and the angle between them - remember, it must be the angle between them - you can use the Law of Cosines to find the third side. In Example 6, what you're given is two angles and a side, so you'll use the Law of Sines, which says simply that the sines are proportional to the opposite sides. Here the side you're looking for BC, is opposite the 108∘. The side you're given, AC, is opposite the unlabeled angle, which measures 180−108−38=34 degrees. Now you can set up the proportion.
BCsinA=ACsinB
BCsin108∘=5.0sin34∘
BC=5sin108∘sin34∘≈8.5
The answer is (D).
|
Similar Questions
Knowledge Check
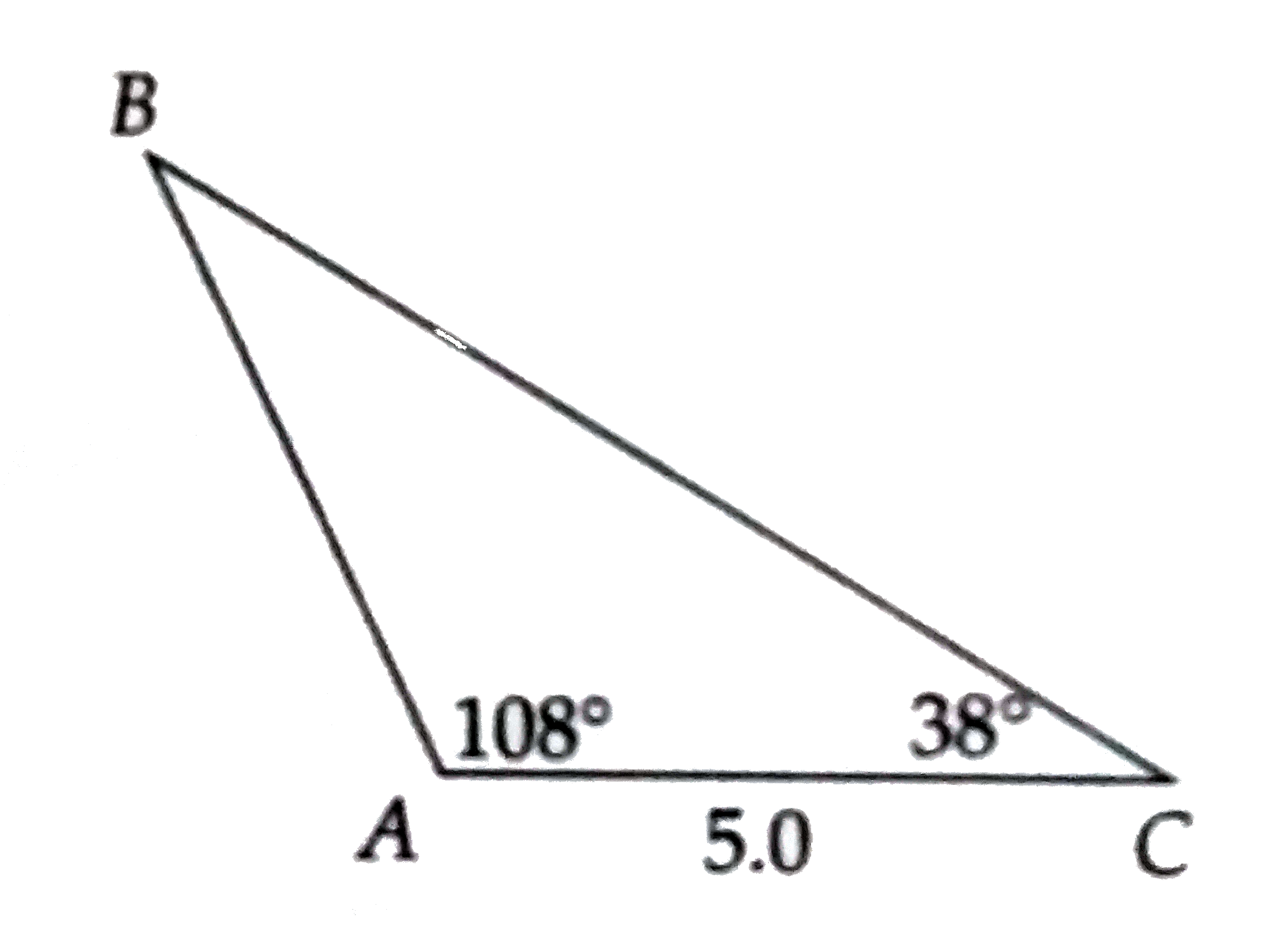
In the figure, if AB = 10, what is the length of the side CD ?
 A5B5√3C10√3D10
A5B5√3C10√3D10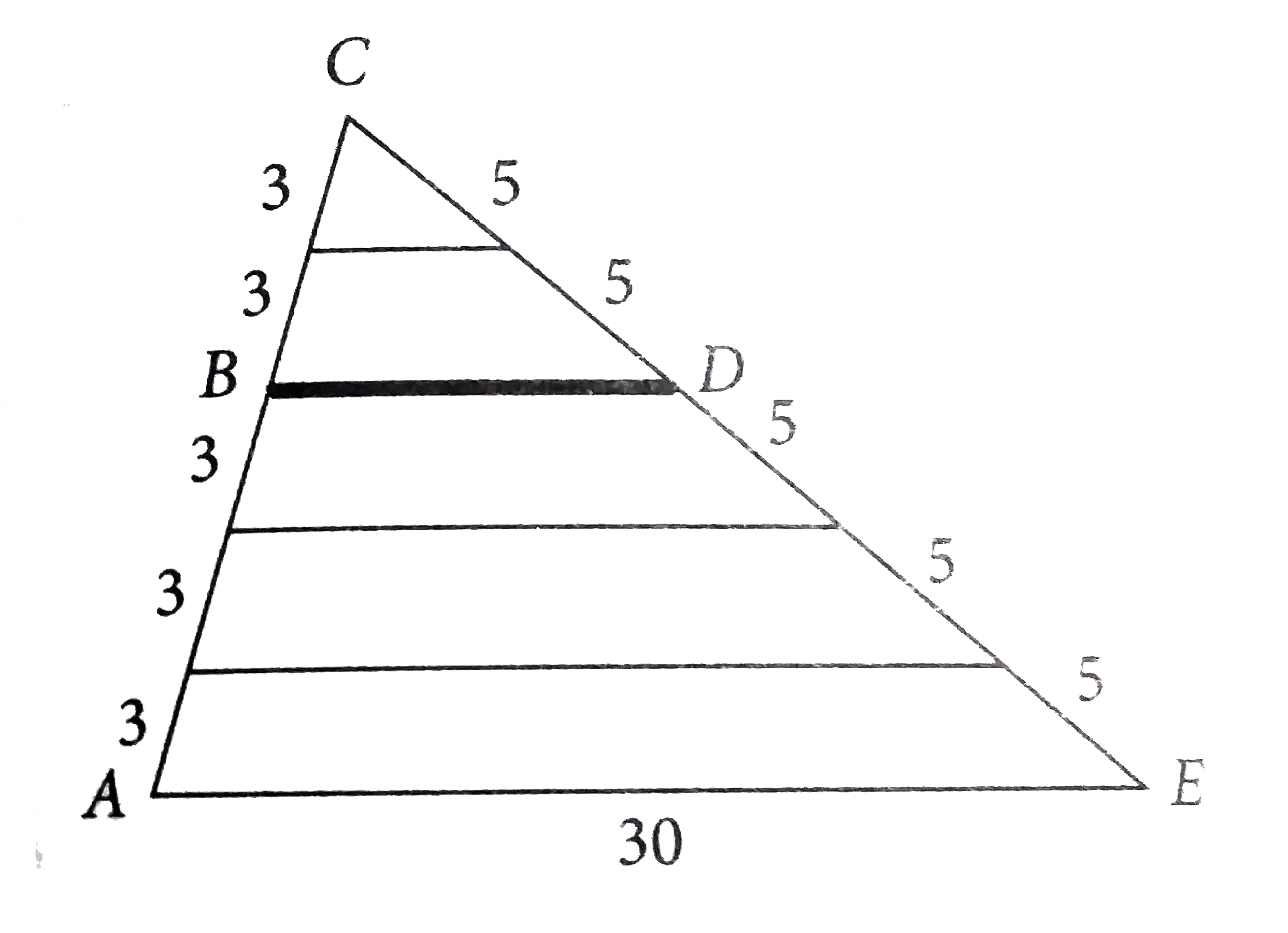
In the figure above , what is the length of ¯¯¯¯¯¯BD?A8B9C12D15In the figure shown below, E and G lie on ¯¯¯¯¯¯AC, D and F lie on ¯¯¯¯¯¯AB,¯¯¯¯¯¯DEand¯¯¯¯¯¯FG are parallel to ¯¯¯¯¯¯BC, and the given lengths are in feet. What is the length of ¯¯¯¯¯¯AC, in feet?
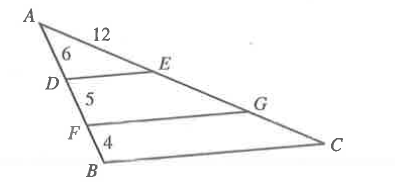 A9B18C21D30
A9B18C21D30

If AD=2CD,andDB=BC=6, what is the length of side AB?
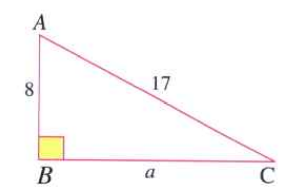
View SolutionFind the length of side BC in the given triangle.
View SolutionIn a ΔABC,D,EandF are respectively the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, find the permeter of ΔDEF.
View SolutionIn the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
View SolutionAD is the longest side of the triangle ABD shown in the figure. What is the length side of ΔABC ?
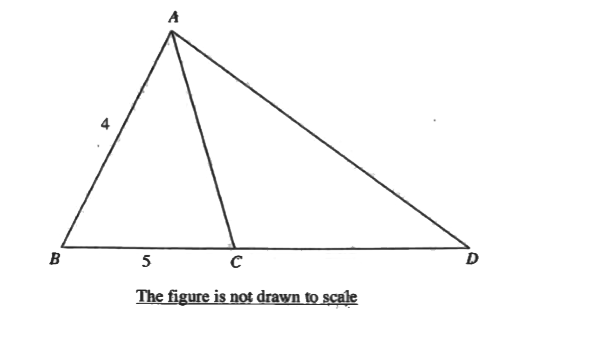
View Solution