For what value of x will f(x)=(1−2x)2 have the minimum value ?
A
−1
B
−12
C
0
D
12
Video Solution
Text Solution
The correct Answer is:D
The expression (1−2x)2 is something squared. A real number squared cannot be smaller than 0. This function will have its minimum value when the part inside the parentheses is zero :
1−2x=0
−2x=−1
x=12
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
For what value of x is ∣∣16−(x+5)2∣∣ at its minimum ?
A−9B−5C5D9 - Question 2 - Select One
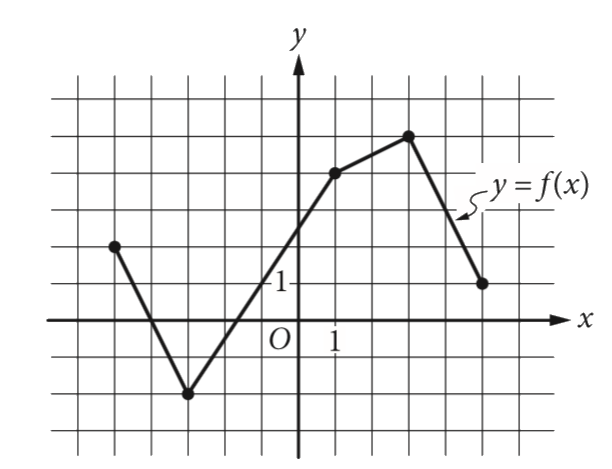
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?A−5B−3C−2D3
Find the largest natural number a for which the maximum value of f(x)=a−1+2x−x2 is smaller than the minimum value of g(x)=x2−2ax+10−2a.
View SolutionLet f(x)=∣∣x2−3x−4∣∣,−1≤x≤4 Then f(x) is monotonically increasing in [−1,32] f(x) monotonically decreasing in (32,4) the maximum value of f(x)is254 the minimum value of f(x) is 0
View Solutionf(x)=x2+1x2−6x−6x+2 then min value of f(x)
View SolutionLet P be minimum value of 9sin2x+16cosec2x and S be the minimum value of 16sin2x+9cosec2x then the value of P+S2 is
View SolutionMinimum value of of f (x)=2x2−4x+5is
View SolutionIf the maximum value of ||x−3|−|x−2∣∣ is a and minimum value of |x−1|+|x−2| is b, then find the value of (a+b).
View Solution

