If point P(3, 2) is rotated 90 degree counterclockwise with respect to the origin, what will be its new coordinates ?
The correct Answer is:A
To find the new coordinates of point P(3, 2) after a 90-degree counterclockwise rotation about the origin, we can use the following steps:
Step 1: Understand the rotation transformation
When a point (x, y) is rotated 90 degrees counterclockwise about the origin, the new coordinates (x', y') can be found using the transformation:
x′=−y
y′=x
Step 2: Identify the original coordinates
The original coordinates of point P are:
x=3,y=2
Step 3: Apply the transformation
Now, we will apply the transformation to find the new coordinates:
1. Calculate x′:
x′=−y=−2=−2
2. Calculate y′:
y′=x=3
Step 4: Write the new coordinates
After applying the transformation, the new coordinates of point P after the rotation are:
P′(−2,3)
Conclusion
The new coordinates of point P(3, 2) after a 90-degree counterclockwise rotation about the origin are (−2,3).
When a point (x, y) is rotated 90 degrees counterclockwise about the origin, the new coordinates (x', y') can be found using the transformation:
x′=−y
y′=x
The original coordinates of point P are:
x=3,y=2
Now, we will apply the transformation to find the new coordinates:
1. Calculate x′:
x′=−y=−2=−2
2. Calculate y′:
y′=x=3
After applying the transformation, the new coordinates of point P after the rotation are:
P′(−2,3)
The new coordinates of point P(3, 2) after a 90-degree counterclockwise rotation about the origin are (−2,3).
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
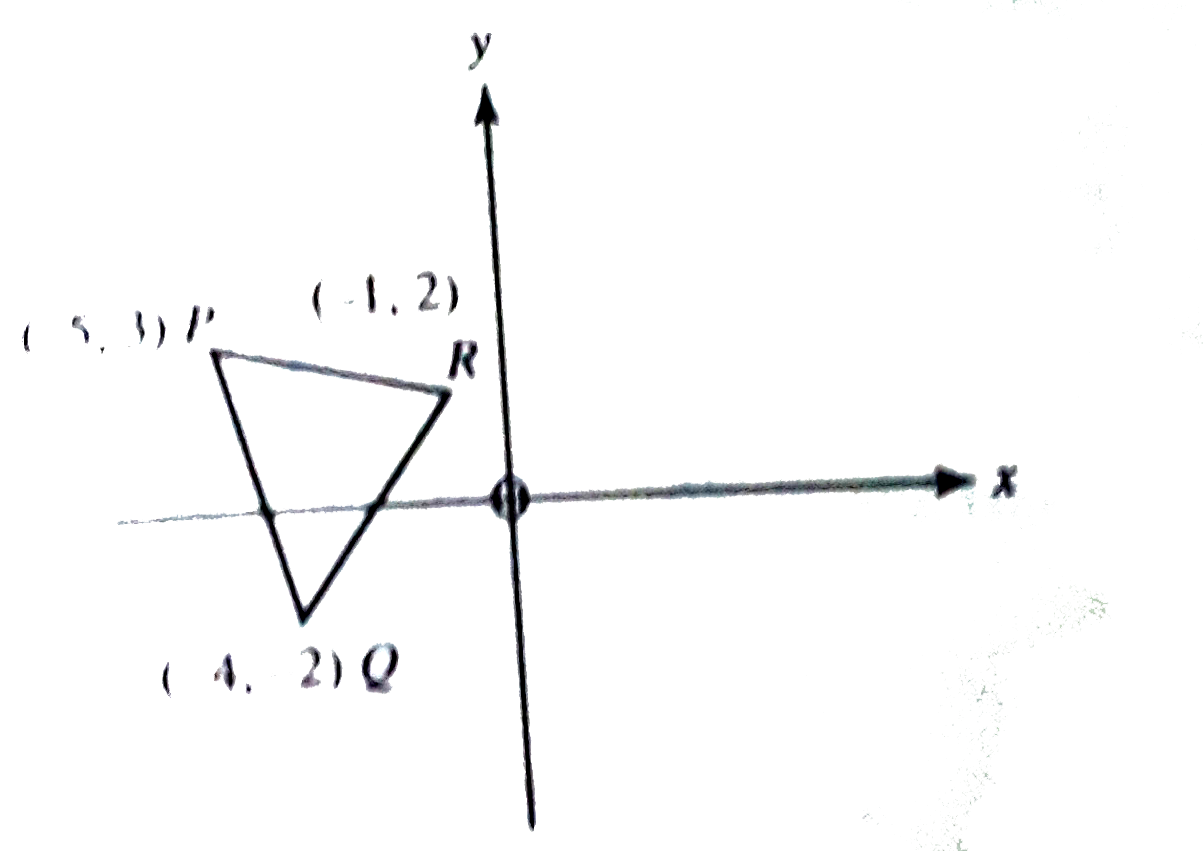
Triangle PQR , shown in the diagram above , is translated 4 units to the right and 5 units down. The resulting triangle is then rotated 180∘ counterclockwise about the origin. What is the final image of point P ?A(-1,-2)B(1,2)C(2,1)D(-2,1) - Question 2 - Select One
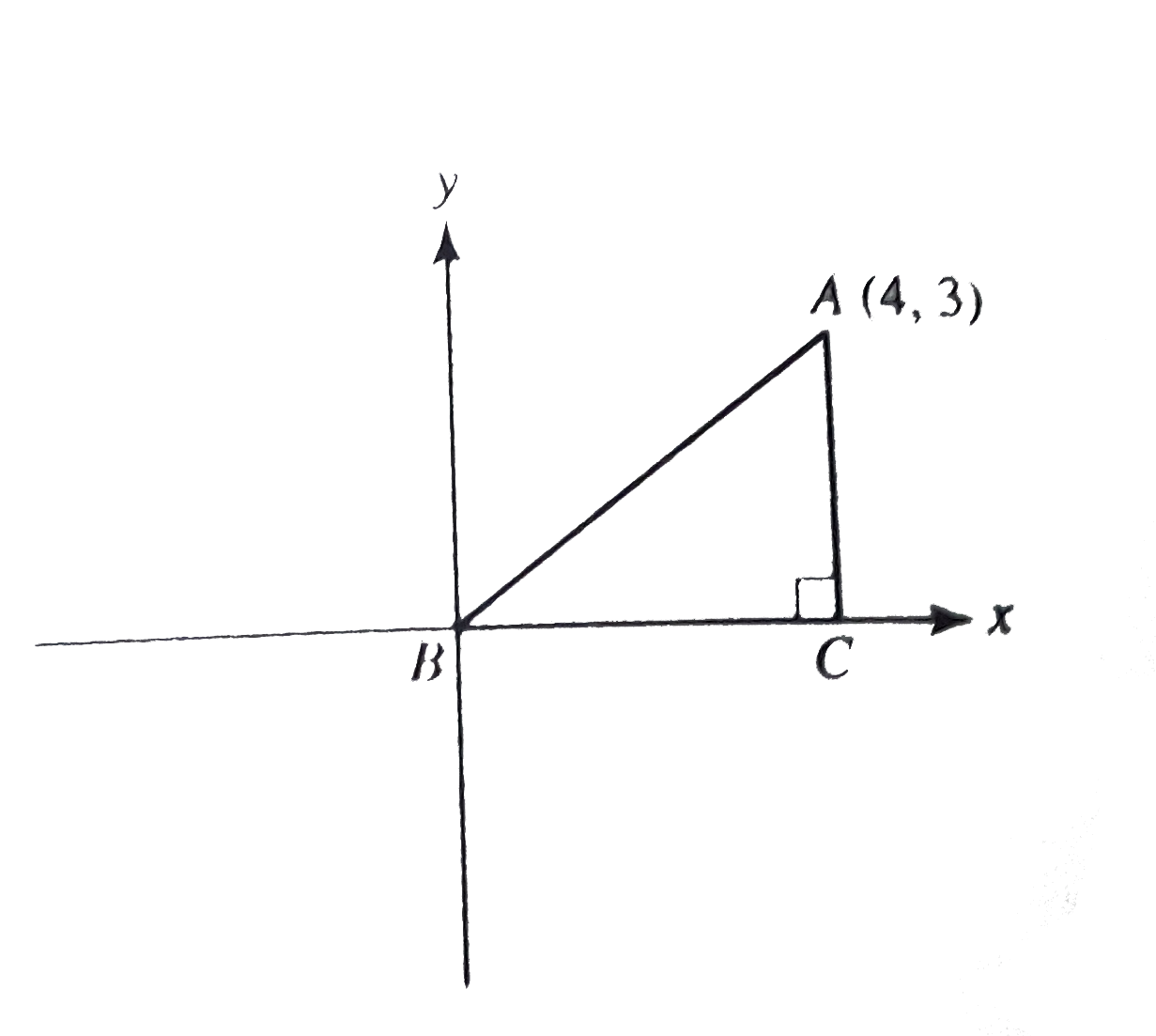
In the figures above , △ABC is rotated counterclockwise through 90∘ about the origin. Its image is △A'B'C'. What is the slope of ¯¯¯¯¯¯¯¯¯A'B' ?A34B43C−34D−43
The point P(1,1) is transiated parallel to 2x=yin the first quadrant through a unith distance. The coordinates of the point in new position are
View SolutionThe line joining two points A(2,0) and B(3,1) is rotated about A in anticlockwise direction through an angle of 15∘. find the equation of line in the new position. If b goes to c in the new position what will be the coordinates of C.
View SolutionThe line joining two points A(2,0) and B(3,1) is rotated about A in anticlockwise direction through an angle of 15∘. find the equation of line in the new position. If b goes to c in the new position what will be the coordinates of C.
View SolutionThe line joining two points A(2,0) and B(3,1) is rotated about A in anticlockwise direction through an angle of 15∘. find the equation of line in the new position. If b goes to c in the new position what will be the coordinates of C.
View SolutionIf the axes are rotated through an angle of 45∘ in the clockwise direction, the coordinates of a point in the new systeme are (0,-2) then its original coordinates are
View SolutionIf the origin is shifted (1,2,−3) without changing the directions of the axis, then find the new coordinates of the point (0,4,5) with respect to new frame.
View Solution

