Doubtnut Promotions Sticky

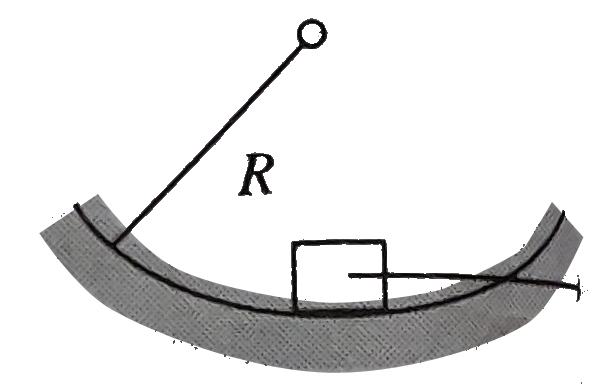
A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is

A

R2

B

(1−√32)R

C

√32R

D

3R8

Text Solution
Verified by Experts

The correct Answer is:B

h=R−Rcosθ,μ=Tanθ

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 11PHYSICSNEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    A partical is placed at rest inside a hollow hemisphare of redius R. The coefficient of friction between the partical and the homisphere is μ=1√3. The maximum height up to which the partical can remain stationary is

    AR2
    B(1−√32)R
    C√32R
    D3R8
  • Question 2 - Select One

    The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is

    Ar√1+μ2
    Br[1−1√1+μ2]
    Cr√1+μ2
    Dr[√1+μ2−1]
  • Question 3 - Select One

    A particle is released from the top of the smooth hemisphere R as shown.
    the normal contact between the particle and the hemisphere in position θ is
    ocr_image

    Amg(3−2cosθ)
    Bmg(3cosθ−2)
    Cmg(4cosθ−3)
    Dmg(4−3cosθ)