One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
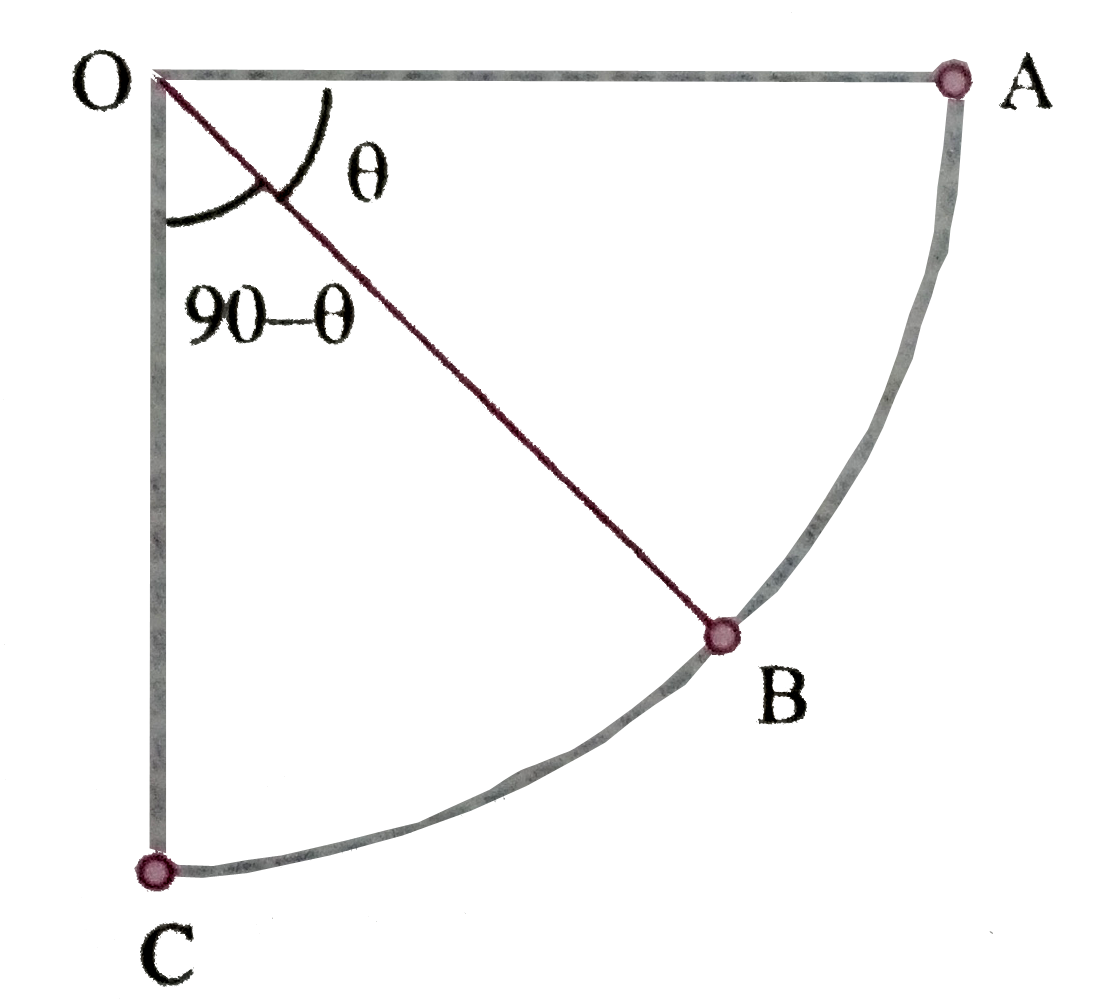
If |→vC=2|→vB∣ then the value of θ as shown is
cos−1(14)
sin−1(14)
cos−1(12)
sin−1(12)
The correct Answer is:B
vB=√2gLsinθ and vC=√2gL
if VC=2vB
Then 2gL=4(2gLsinθ)
or sinθ14orθsin−1(14)
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0130videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-0230videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS107videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
One end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
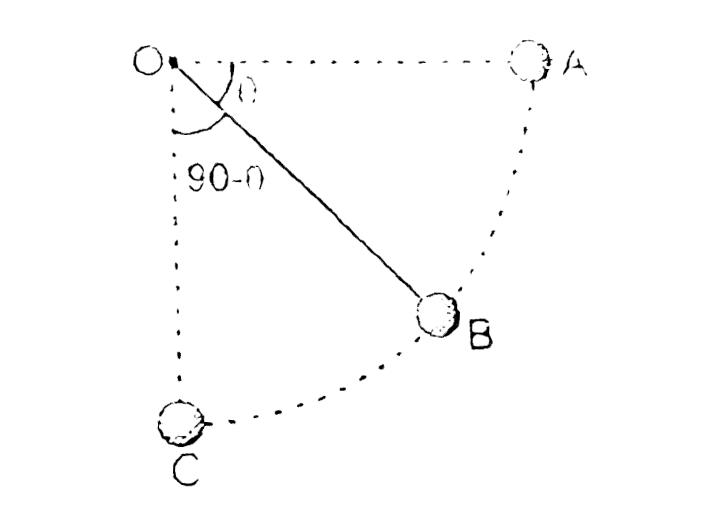
if |→vc|=2|→vB| then the value of θ shown isView SolutionOne end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vc|=2|→vB| thenView Solution
Knowledge Check
- Question 1 - Select One
One end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vc|=2|→vB| thenAt1>t2Bt1<t2Ct1=t2DInformation is insufficient. - Question 2 - Select One
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vC=2|→vB∣ then the value of θ as shown isAcos−1(14)1/3Bsin−1(14)1/3Ccos−1(12)1/3Dsin−1(12)1/3 - Question 3 - Select One
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position B to lowest position C is t2. Let the velocity of ball at B is →vB and C is →vC respectively.

If |→vC|=|→vB| then the value of θ as shown isAcos−1(1)4Bsin−1(1)4Ccos−1(1)2Dsin−1(1)2
A ball of mass 1.00 kg is attached to a loose string fixed to a ceiling. The ball is released from rest and falls 2.00 m, where the string suddenly stops it. Find the impulse on it from the string.
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
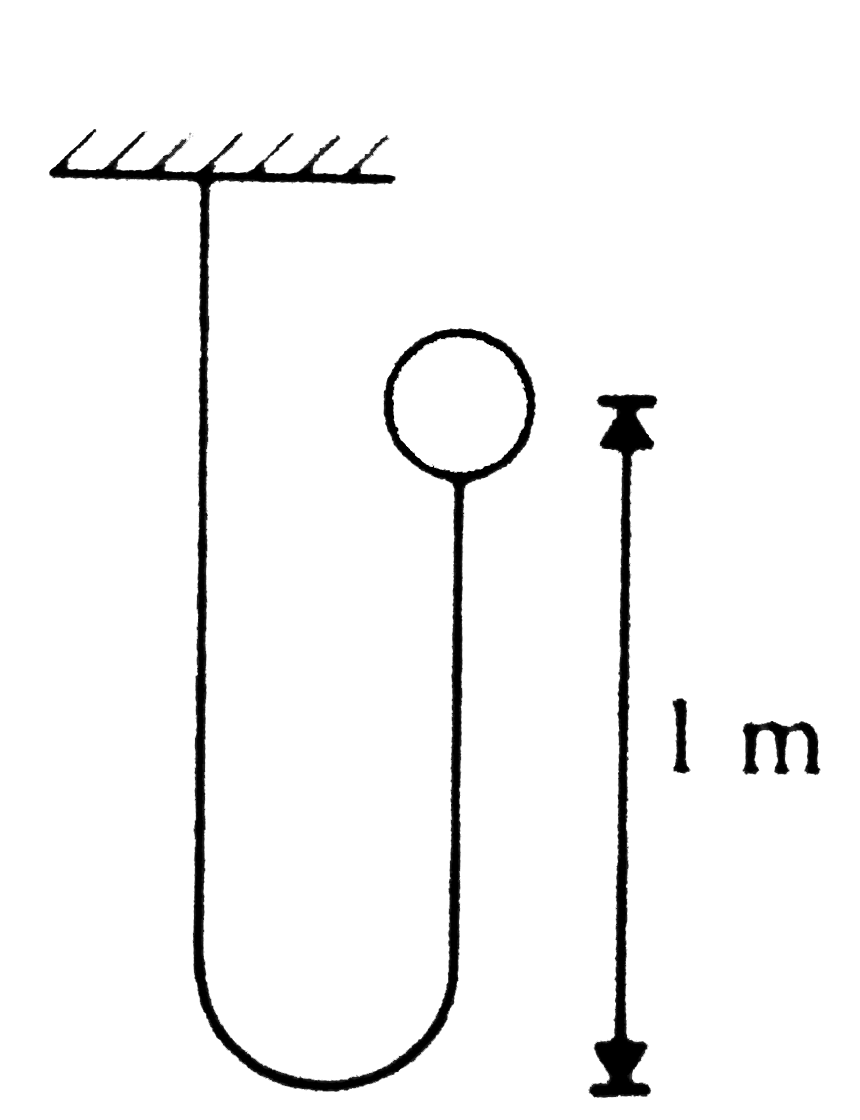 View Solution
View Solution
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.View SolutionOne end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position B to lowest position C is t2. Let the velocity of ball at B is →vB and C is →vC respectively.

If |→vC−→vB|=|→vB|, then the value of θ as shown is :View SolutionOne end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position B to lowest position C is t2. Let the velocity of ball at B is →vB and C is →vC respectively.
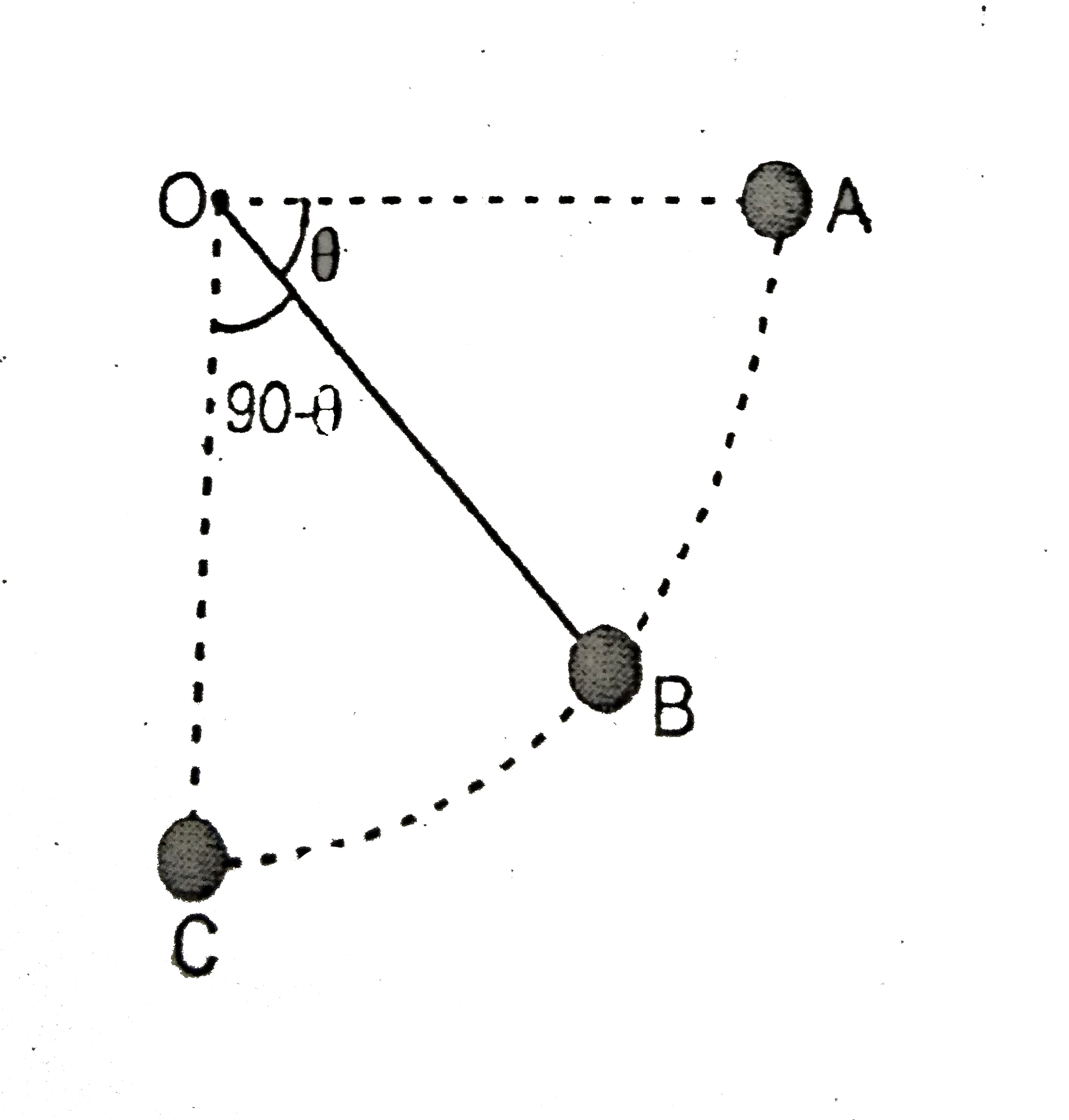
If |→vC|=|→vB| then :View Solution

