One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position B to lowest position C is t2. Let the velocity of ball at B is →vB and C is →vC respectively.
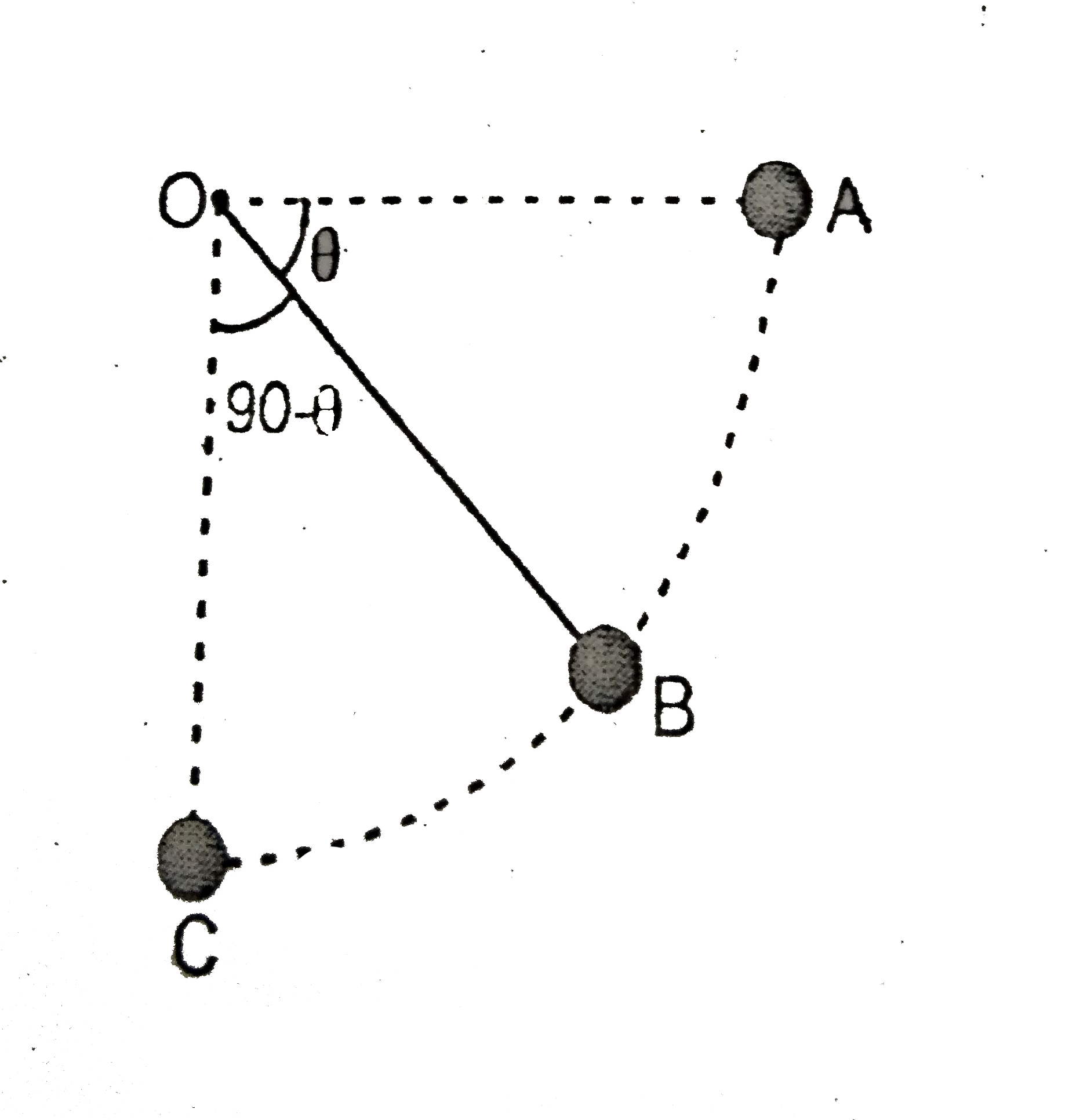
If |→vC|=2|→vB| then :
t1>t2
t1<t2
t1=t2
information insufficient
The correct Answer is:B
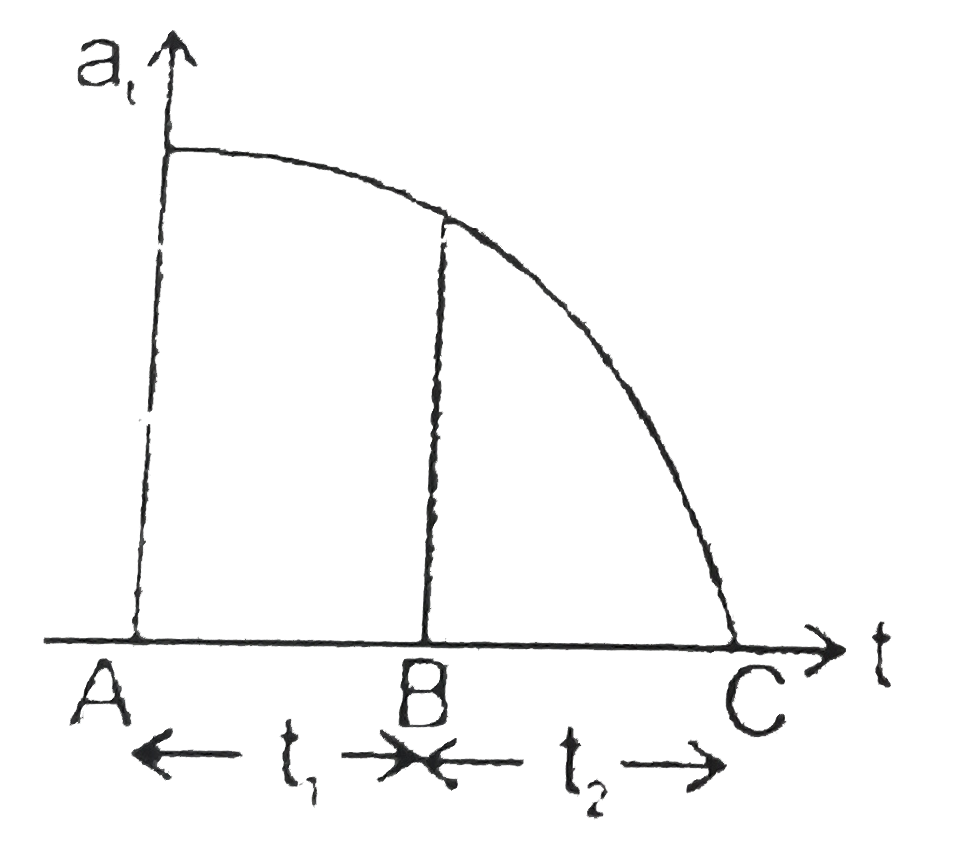
Tangential acceleration is at=gcosθ
which decreases with time.
Hence the plot of at versus time may be as shown in graph. Area under graph in time interval t1=vB−0=vB
Area under graph in time interval t2=vC−vB=vB
Hence area under graph in time t1 and t2 is same.
∵t1>t2
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0130videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-0230videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS107videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
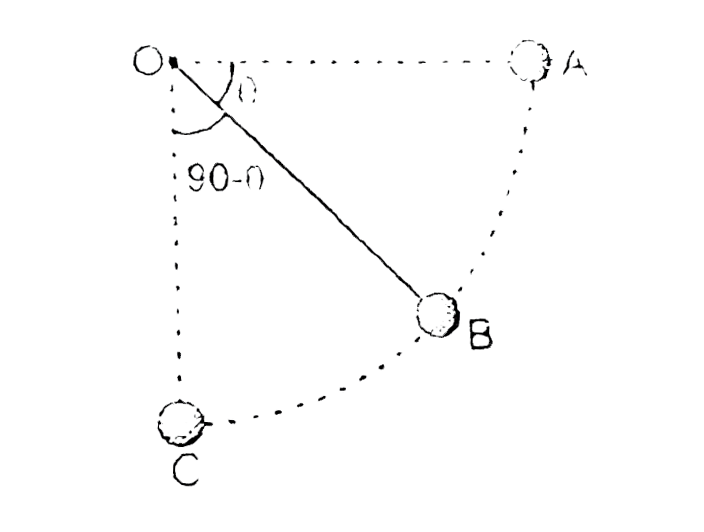
One end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vc|=2|→vB| thenView SolutionOne end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
if |→vc|=2|→vB| then the value of θ shown isView Solution
Knowledge Check
- Question 1 - Select One
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position B to lowest position C is t2. Let the velocity of ball at B is →vB and C is →vC respectively.

If |→vC−→vB|=|→vB|, then the value of θ as shown is :Acos−1(14)1/3Bsin−1(14)1/3Ccos−1(12)1/3Dsin−1(12)1/3 - Question 2 - Select One
One end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vc|=2|→vB| thenAt1>t2Bt1<t2Ct1=t2DInformation is insufficient. - Question 3 - Select One
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
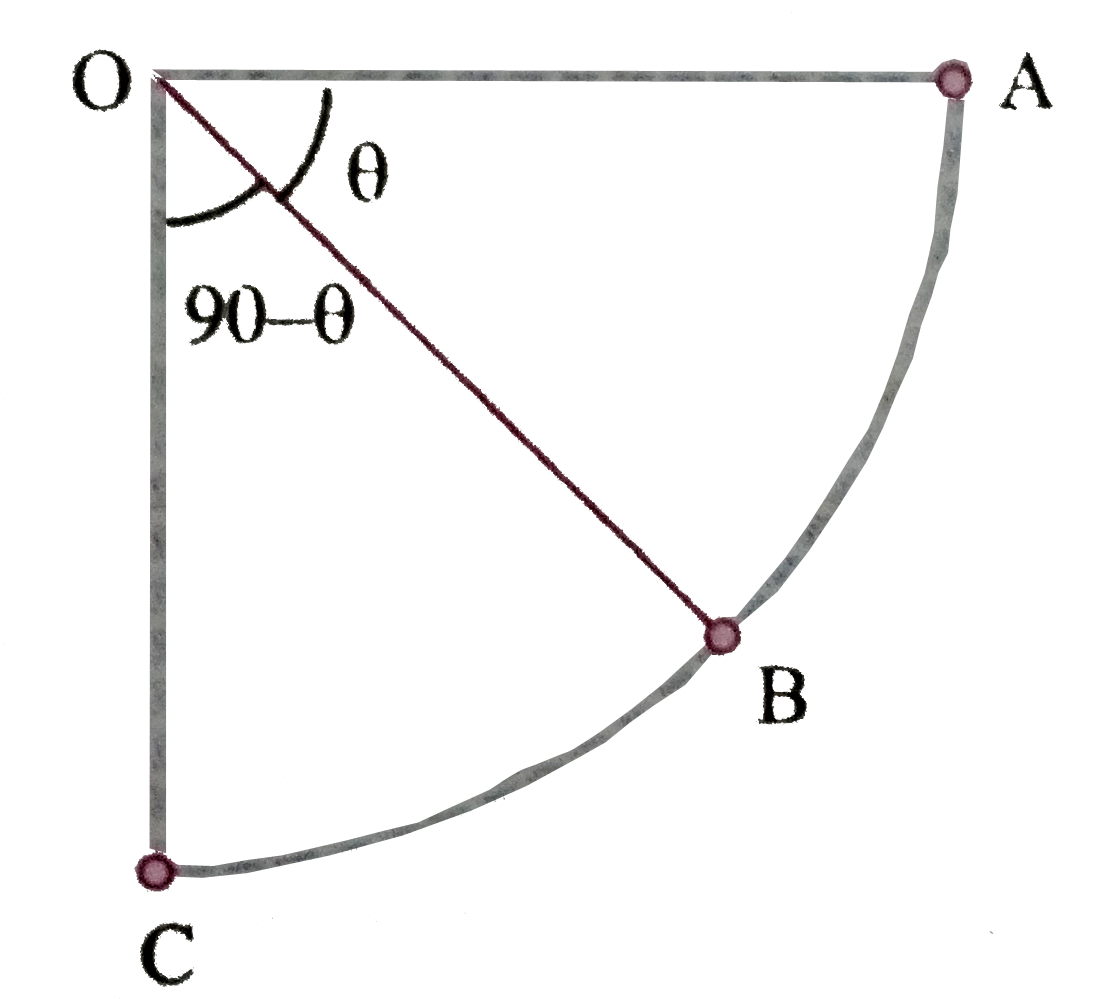
If |→vC=2|→vB∣ then the value of θ as shown isAcos−1(1)2Bsin−1(14)Ccos−1(1)2Dsin−1(1)2
A ball of mass 1.00 kg is attached to a loose string fixed to a ceiling. The ball is released from rest and falls 2.00 m, where the string suddenly stops it. Find the impulse on it from the string.
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
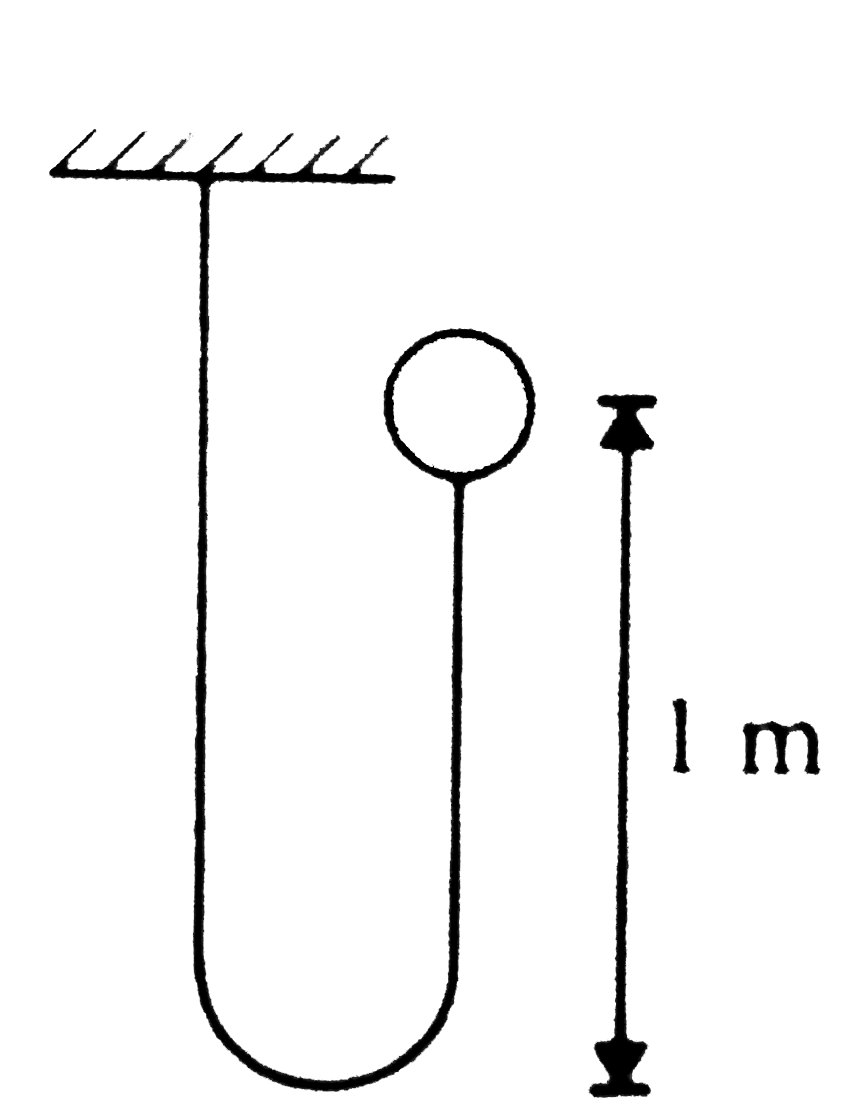 View Solution
View Solution
A ball is attached to a string of length L and the ball is given velocity v0 at its lowest point. Find the speed of the ball at point B,C and D. Assume that the ball is moving in vertical circle.View SolutionOne end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vC=2|→vB∣ then the value of θ as shown isView SolutionA heavy particle is attached to one end of a string 1m long whose other end is fixed at O. It is projected from it lowest position horizontally with a velocity V:
View Solution

