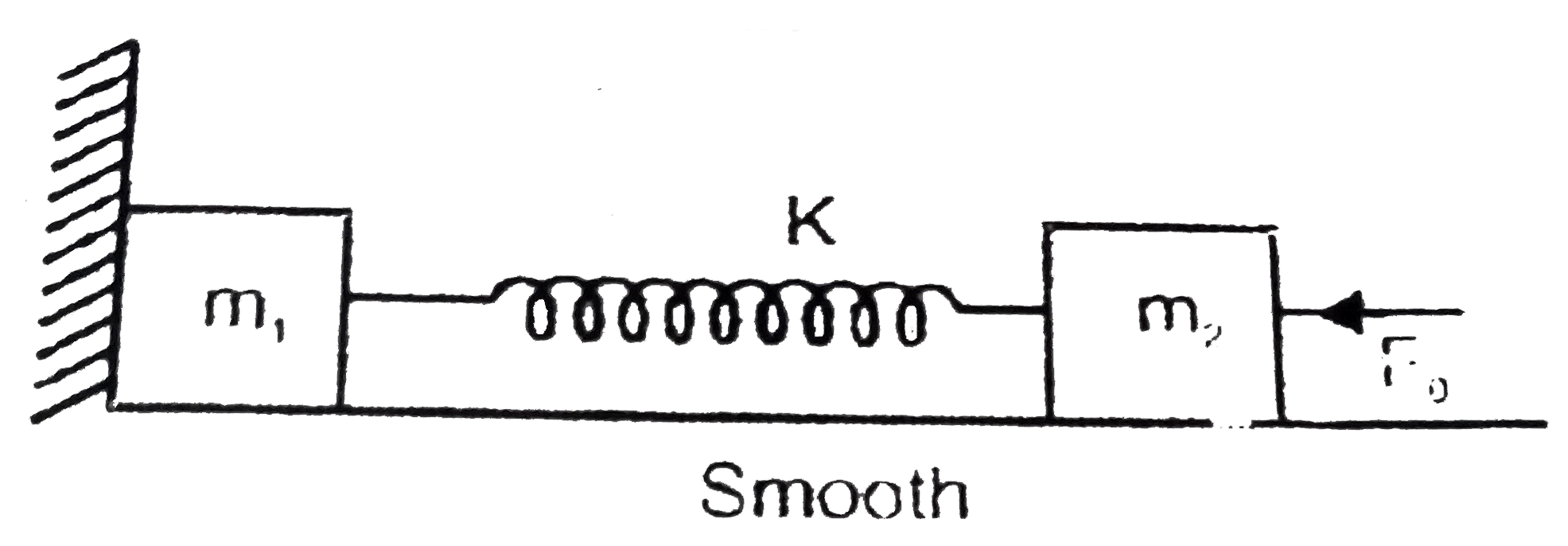
Given system is in equilibrium. All surfaces are smooth. Spring is ideal and blocks are sticked at the ends of spring Now F0 is removed Average normal contact force between wall and mass m1 upto the time spring attains its natural length for the first time in newton is (given that F0=2π Newton)
The correct Answer is:4
if J is the impulse imparted to the m2 by spring after removal of F0 (up to the spring attains its natural length for the first time.)
J22m2=12K(F0K)2=F202K
J=F0√m2K
Same impulse is imparted to m1 by wall.
time requried
=T4=142π√m2K=π2√m2k
<N≥JT4=F0√m2Kπ2√m2k=2F0π
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0130videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-0230videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS107videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
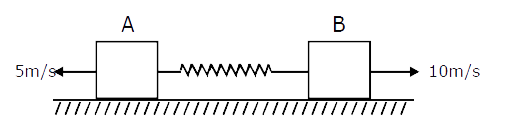
The two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
 View Solution
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2 . Find the time period and amplitude of resultant motion. (Given : spring constant is K.)
View Solution
Knowledge Check
- Question 1 - Select One

A spring having a spring constant k is fixed to a vertical wall as shown in Fig. A block of mass m moves with velocity v torards the spring from a parallel wall opposite to this wall. The mass hits the free end of the spring compressing it and is decelerated by the spring force and comes to rest and then turns the spring is decelerated by the spring force and comes to rest and then turns back till the spring acquires its natural length and contact with the spring is broken. In this process, it regains its angular speed in the opposite direction and makes a perfect elastice collision on the opposite left wall and starts moving with same speed as before towards right. The above processes are repeated and there is periodic oscillation.
Q. What is the time period of oscillation ?Aπ√mkB√πmk+LmCπ√mk+2LvDπ√mk+Lv - Question 2 - Select One or More
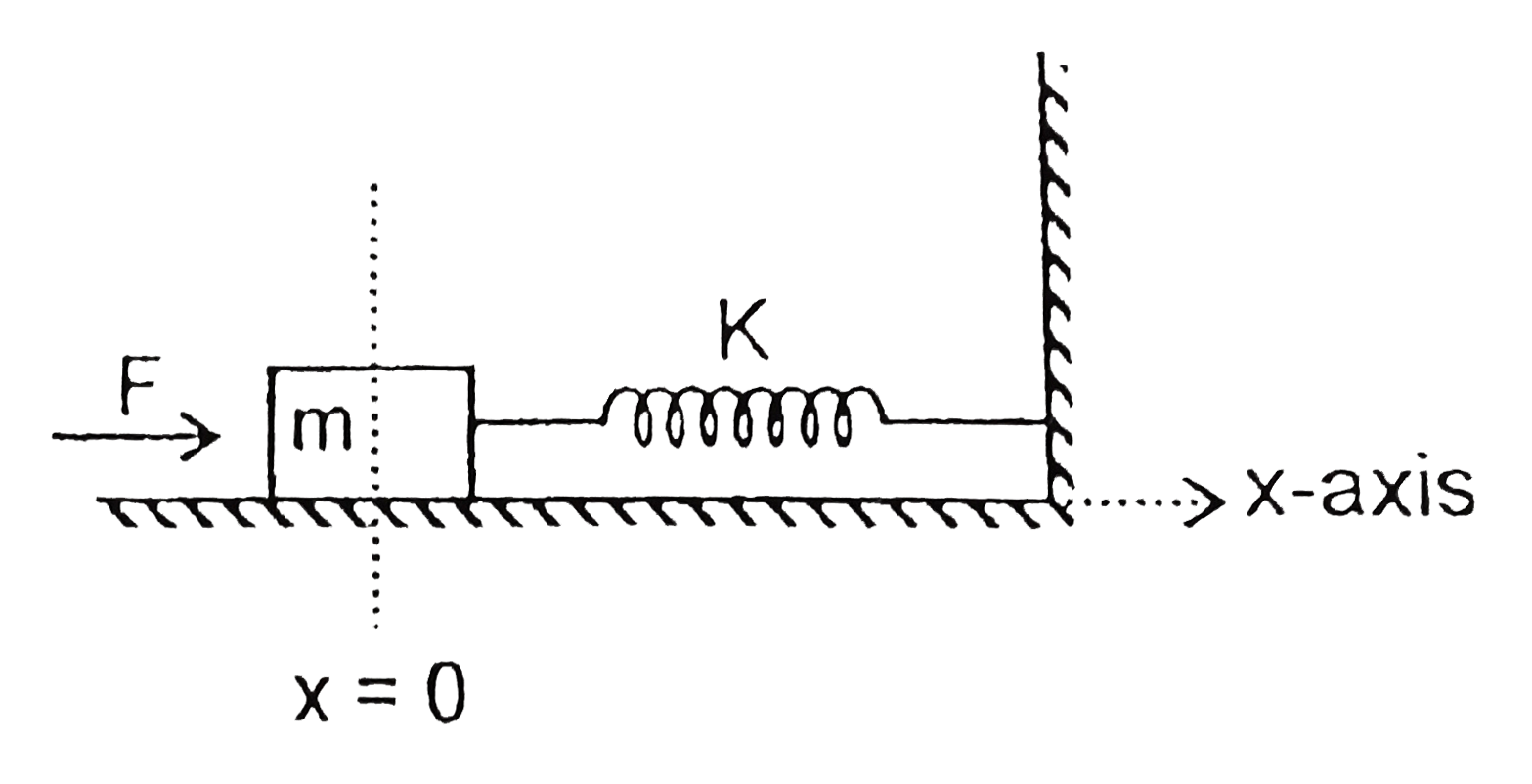
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ thenAMotion of block is SHMBTime period of motion is π√mk[√2+√23]CTime period of motion is π√mk[1+√32]DSum of potential energy and kinetic energy of spring block system is maximum at right extreme. - Question 3 - Select One or More
Two blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
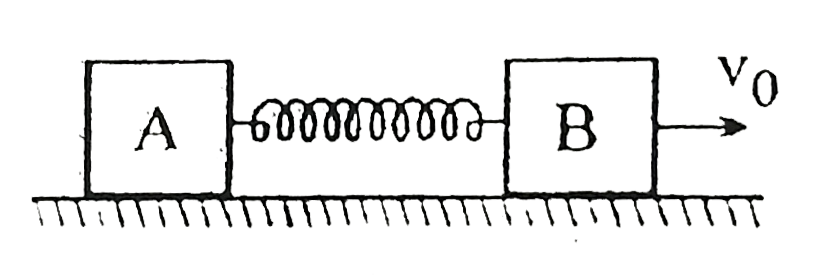 Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Athe maximum velocity of B will be v0Bas seen from ground, A can move towards right onlyCthe spring will have maximum extension when A and B both stopDthe spring will be at natural length again when B is at rest
Two blocks of masses m and 2m compress a spring of spring constant k by x0 and blocks are a connected by a thread and placed on a smooth surface as shown. Now , thread is burned. Find the speed of each block when the spring attains its normal length L.
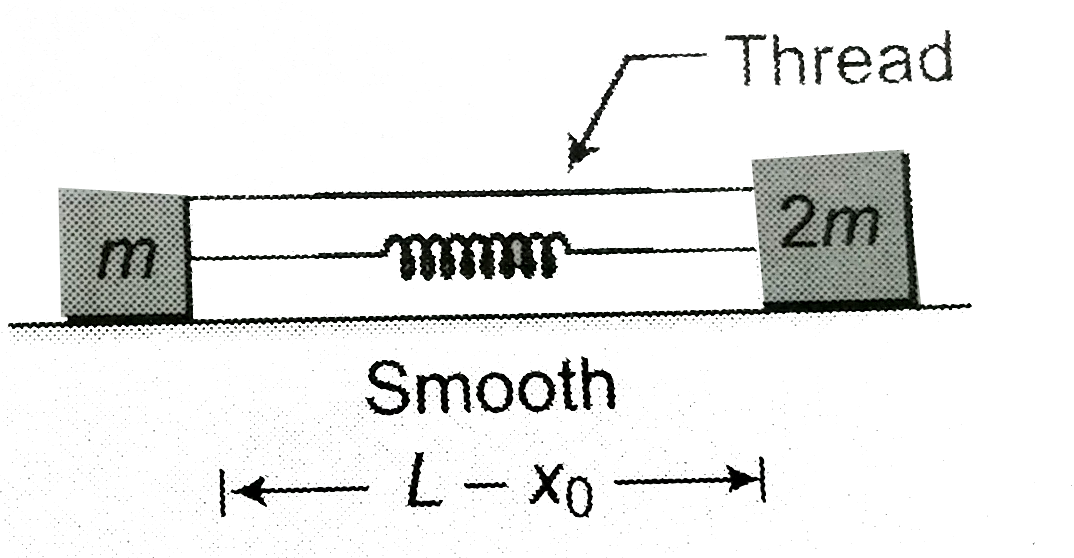 View Solution
View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.
 View Solution
View SolutionThe system is in equilibrium and at rest. Now mass m1 is removed from m2. Find the time period and amplituded of resultant motion. Spring constant is K.
 View Solution
View SolutionA spring has force constant k=200N/m and its one end is fixed. There is a block of mass 2 kg attached to its other end and the system lies on a smooth horizontal table. The block is pulled so that the extension in the spring becomes 0.05 m. At this position the block is projected with a speed of 1m/s in the direction of increasing extension of the spring. Consider time t = 0 at the moment the block is projected and find
(a) the extension (or compression) in the spring as a function of time.
(b) the maximum extension in the spring and the time at which it occurs for the first time.
(c) the time after which the speed of the block becomes maximum for the first time. Given: sin−1(0.446)=0.46 radianView SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 View Solution
View Solution

