Two tangents are drawn from any point P on a given line L=0 to a given circle S=0, if these tangents touch the circle at point A and B, then locus of the circumcentre the ΔPAB will be
A pair of straight lines
A circle touching the given line L=0
A circle touching the given circle S=0
A line parallel to given line L=0
The correct Answer is:D
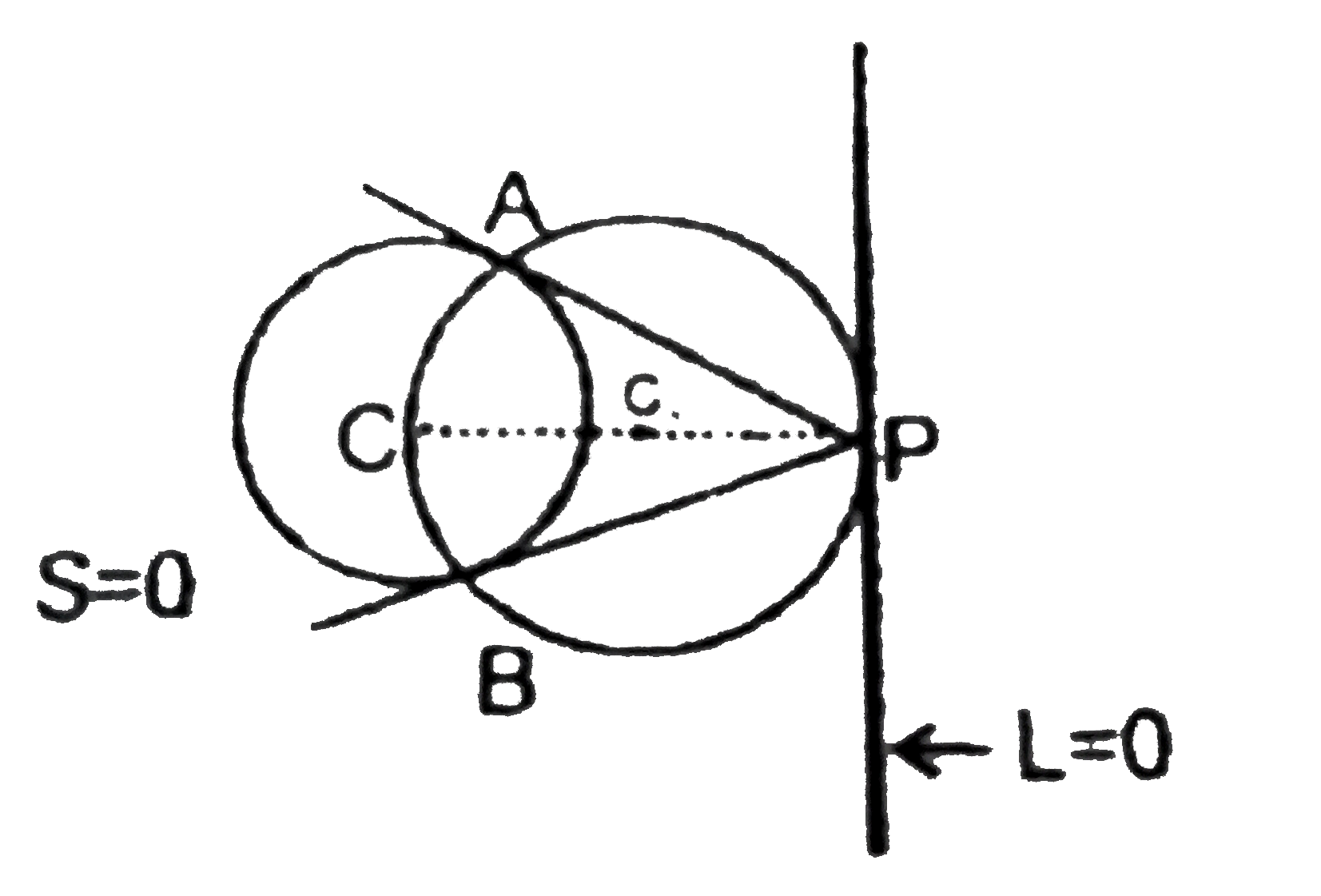
The circumcirle of ΔPAB passes through C with PC as its diameter. Therefore centre of this circle (C1) will be mid pt of PC.
Let L=ax+by+c=0
P(x1.y1)&C(p,q)
C1(h,k)
h=x1+p2
k=y1+q2
p(x1,y1) passes through L=0
⇒ax1+by1+c=0
or a(2h−p)+b(2k−q)+c=0
or 2ah+2bk−ap−bq+c=0
Locus of (h,k) is ax+by=ap+bq+c2
⇒ A line parallel to L=0
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 1
1 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS
9 Videos
- TEST PAPERBOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY
37 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS
131 Videos
Similar Questions
Two tangents are drawn from a point P on the circle at point A and B. O is the centre of the circle. If ∠AOP=60∘ then find ∠APB.
View SolutionTwo circles touch each other at point X. Two common tangents of the circles meet at point P and none of the tangents passes through X. These tangents touch the larger circle at points B and C. If the radius of the larger circle is 15 cm and CP = 20 cm, then what is the radius (in cm) of the smaller circle?
View Solution
Knowledge Check
....... Tangents can be drawn from a point outside a circle.
AZeroBTwoCOneDInfiniteNumber of tangents drawn from a point inside the circle is :
A1B2C4D0Two tangents are drawn from a point P to a circle at A and B. O is the centre of the circle. If ∠AOP=60∘, then ∠APB is
A120∘B90∘C60∘D30∘
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P (1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B the equation of the circumcircle of △PAB is
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution
