A source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. Find the frequency of osund received by the observer at the moment when the source gets closest to him.
The correct Answer is:5
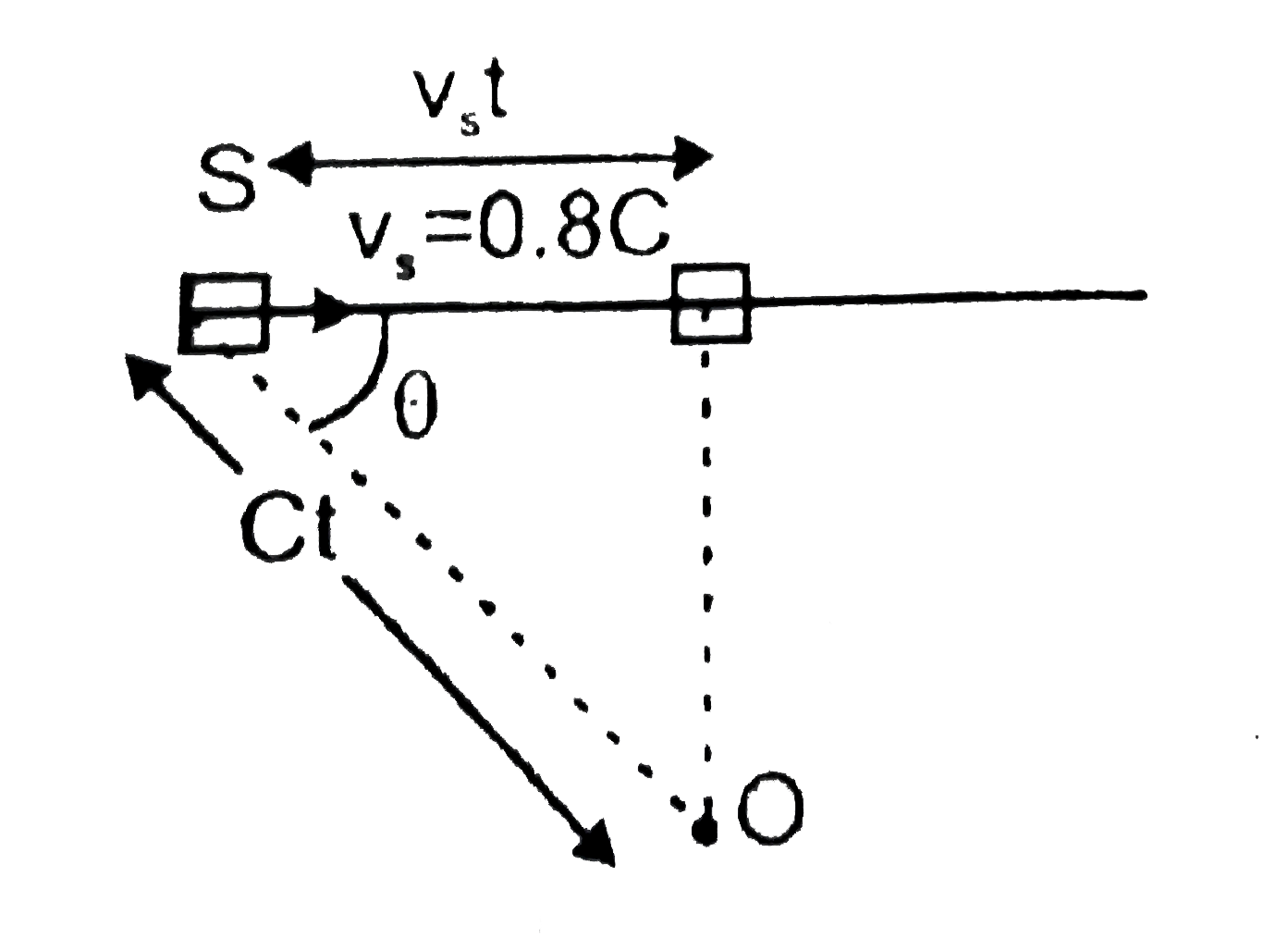
cosθ=VxtCt=0.8
f=f[CC−VScosθ]=1.8[CC−0.8Ccosθ]
=1.811−0.82=1.811−0.64=1.80.36
=18036=5kHz
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-02
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
107 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A source of sound with natural frequency v0 moves uniformly along a straight line separated from a stationary observer by a distance l . The velocity of the source is equal to η fraction of velocityof sound. Find the frequency of sound received by the observer at the moment when the source gets closest to him and also find the distance between the source and the observer at the moment, when the observer receives a frequency v=v0
View SolutionA source of sound of frequency 1.8kHz moves uniformly along a straight line at a distance 250m from observer. The velocity of source is 0.8C where C is the velocity of sound. Find out the frequency of sound received by observer (in kHz) at the moment when the source gets closest to him.
View Solution
Knowledge Check
A source of sound with natural frequency f0=1800Hz moves uniformly along a straight line separated from a stationary observer by a distance l=250m. The velocity of the source is equal to η=0.80 fraction of the velocity of the sound.
Q. The distance between the source and the observer at the moment when the observer receives a frequency f=f0 is
 A640mB420mC320mD250m
A640mB420mC320mD250mA siren of frequency n approaches a stationary observer and then receedes from the observer. If the velocity of source (V)<< the velocity of sound (C), the apparent change in frequency is
A2nV/CB2nC/VCn/VD2VC/nIf a source of frequency n moving with velocity v crosses a stationary observer, then the change in the frequency of sound heard by the observer will be (velocity of sound = V)
A2nVvV2+v2B2nVv(V2−v2)C2nVv(V+v)D2nVv(V−v)
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170ms−1. A detector is placed at a distance of 200 m from the line of motion of the source. (a) Find the frequency of sound received by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant it detects the frequency 1200 Hz. Velocity of sound in air=340ms−1.
View SolutionA source of sound of frequency 1000HZ moves unifornly along a straight line with velocity 0.8 times velocity of sound . An observer is located at a distance l=250m from this line. Find
(a) the frequency of the sound at instant when the source is closest to the observer.
(b) the distance of the source when he observer no change in the frequency.
View SolutionA source of frequency 1 kHz is moving towards a stationary observer with velocity of 0.9 times that of sound. What is the frequency heard by the observer ?
View SolutionA source of sound crosses a stationary observer which is moving with uniform velocity v. If the velocity of sound in air is V, then the ratio of the apparent frequencies heard by the observer before and after the source crosses him would be -
View Solutionwhen a source is going away from a stationary observer with the velocity equal to that of sound in air , then the frequency heard by observer is n times the original frequency . The value of n is
View Solution