In the following figure, OABC is a square. A circle is drawn with as centre which meets OC at P and OA at Q. Prove that:
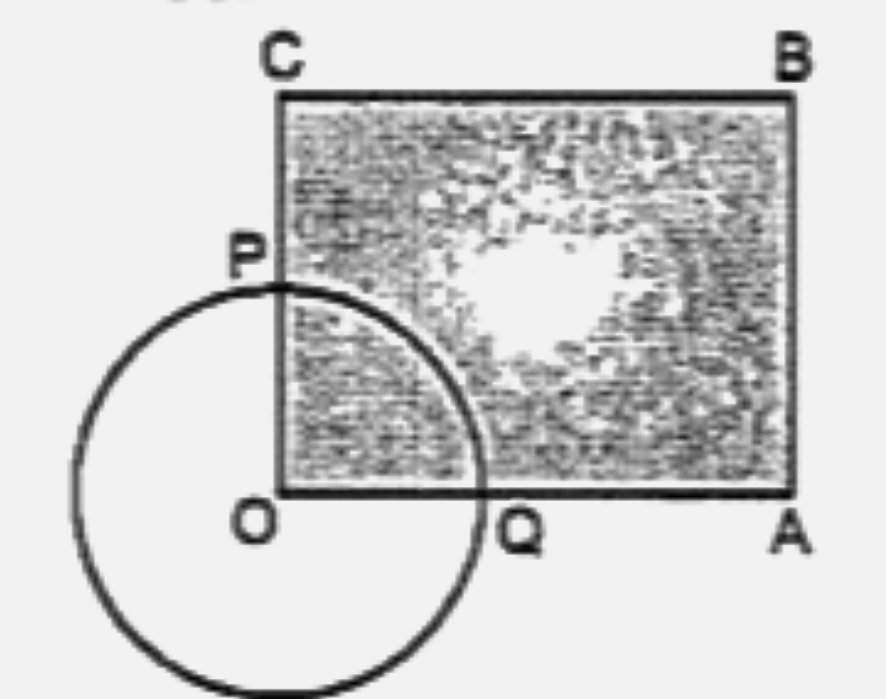
ΔOPA≅ΔOQC
The correct Answer is:OP=OQ
Step by step video & image solution for In the following figure, OABC is a square. A circle is drawn with as centre which meets OC at P and OA at Q. Prove that: Delta OPA ≅ Delta OQC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the following figure, OABC is a square. A circle is drawn with as centre which meets OC at P and OA at Q. Prove that:
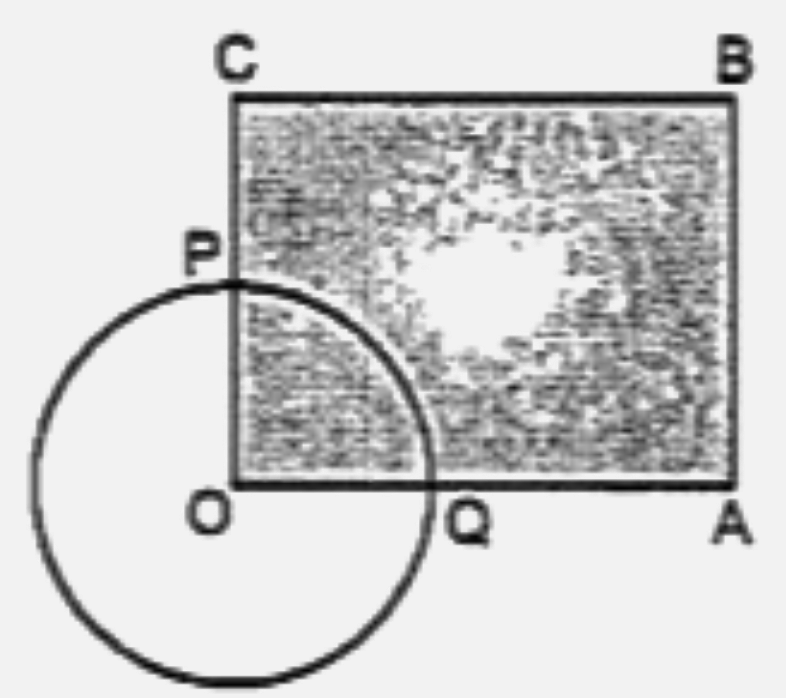
ΔBPC≅ΔBQA
View SolutionIn the following figure, OA=OC and AB=BC.
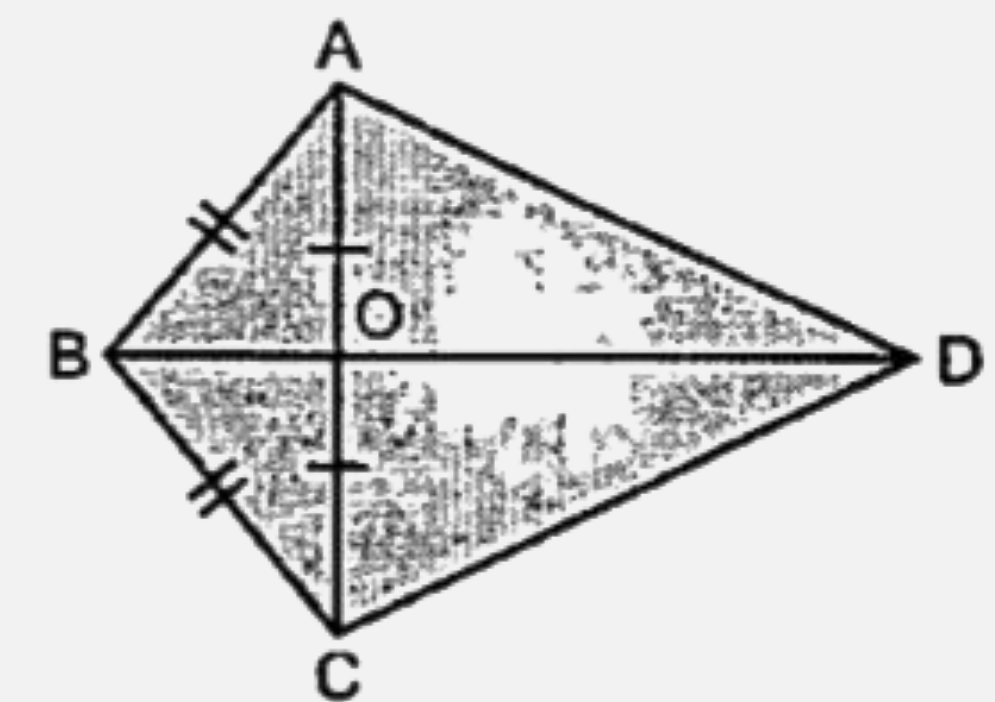
Prove that :
AD=CD
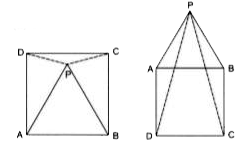
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : ΔAPD≅ΔBPC
(ii) Find the angles of ΔDPC
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of ΔABP= area of □ABCD
View SolutionIn the following figure, OA=OC and AB=BC.
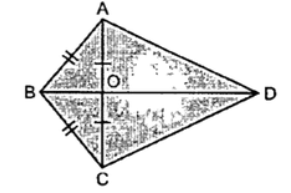
Prove that :
ΔAOD≅ΔCOD
View SolutionBC is an equilateral triangle. A circle is drawn with centre A so that it cuts AB and AC at points M and N respectively. Prove that BN = CM
View SolutionIn the following figure, OA=OC and AB=BC.
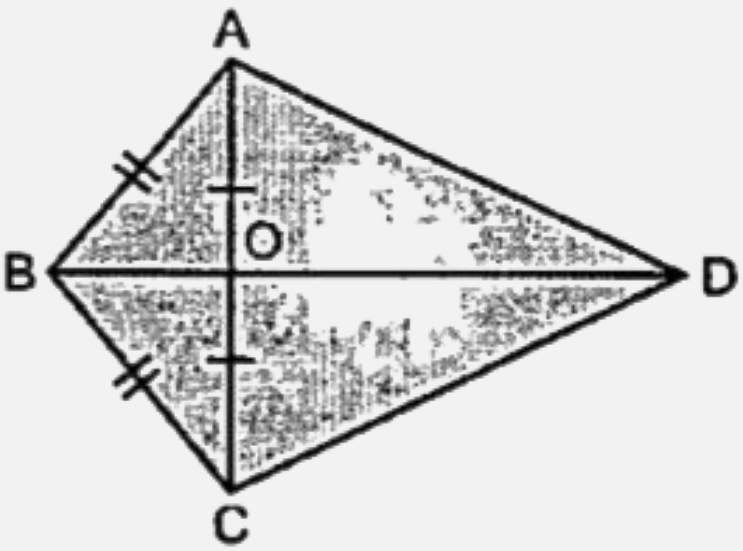
Prove that :
∠AOB=90∘
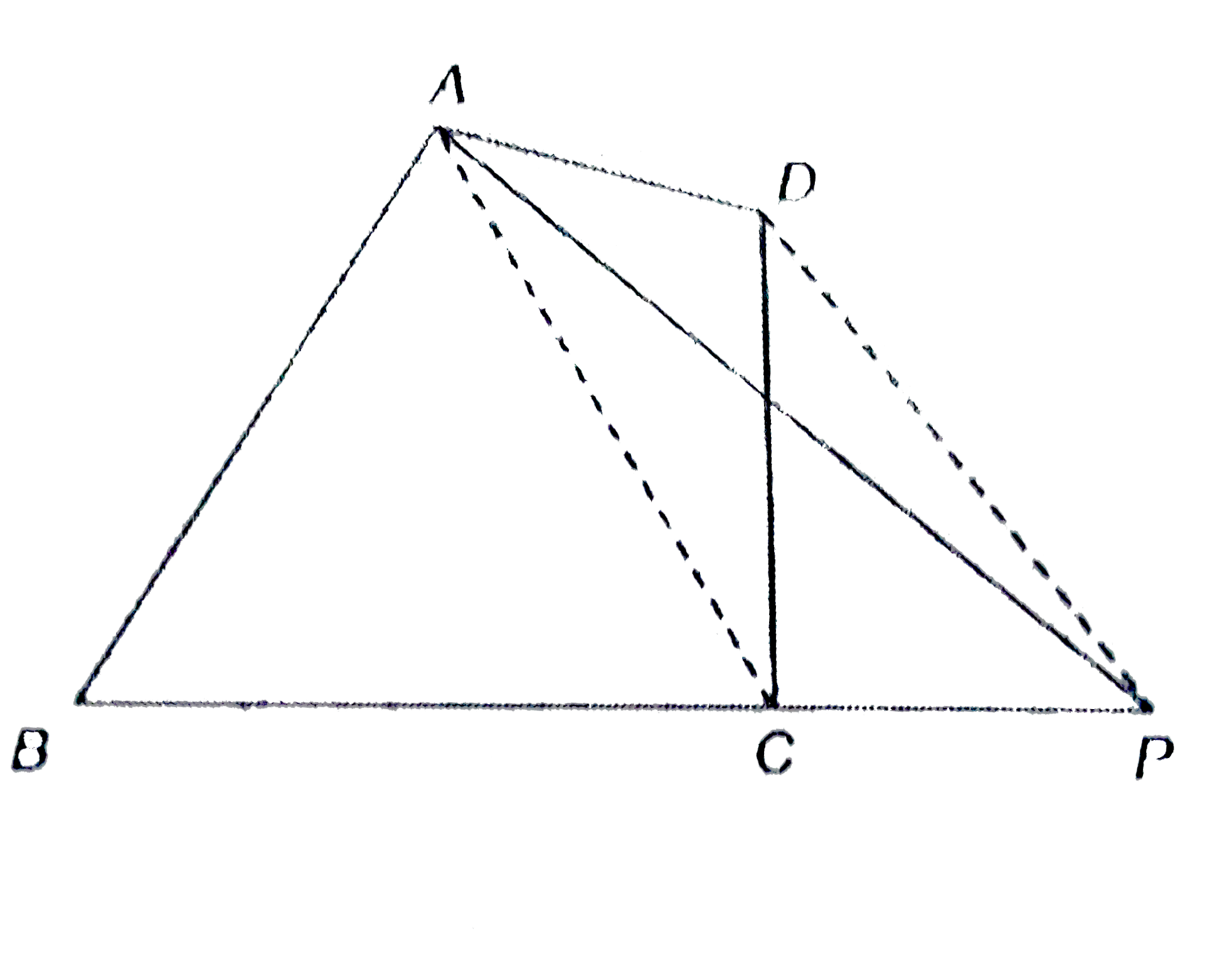
View SolutionIn given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
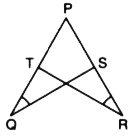
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
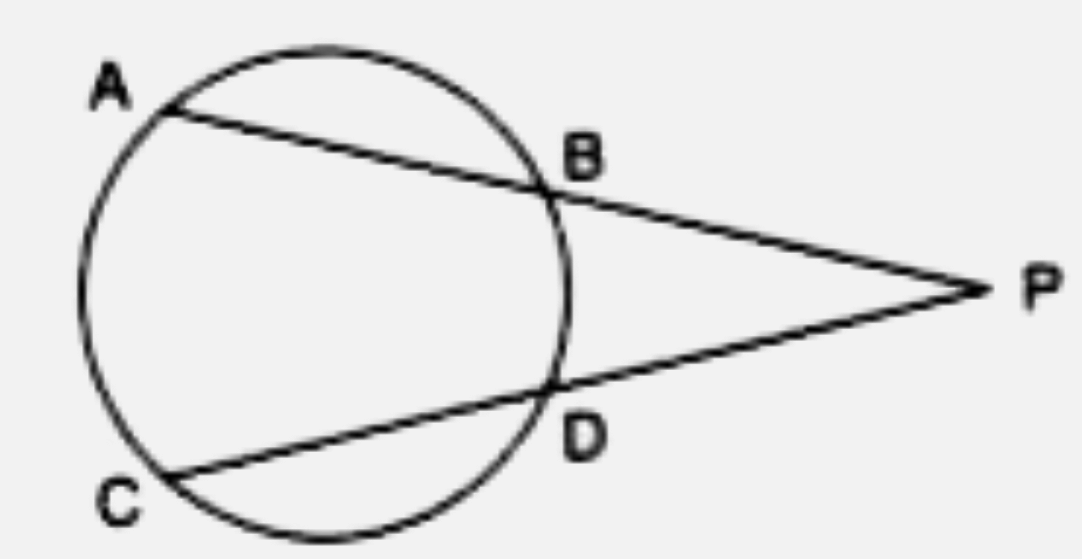
PB=PD
View Solution
