If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
Step by step video & image solution for If P\ a n d\ Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
E and F are the mid-points of the sides AB and CD of a parallelogram ABCD. Prove that the line segment AF and CE trisects BD in three equal parts.
View SolutionP and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
P and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Then which of the following is true?
ACQ is parallel to APBCQ is perpendicular to APCCQ intersects APDNone of these - Question 2 - Select One
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC - Question 3 - Select One
M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
A2 MNB2NMC4 MND4 NM
P is the mid-point of the side AD of the parallelo- gram ABCD. The line BP meets the diagonal AC in Q and the line CD in R. Then RQ:QB is equal to
View SolutionThe middle points of the parallel sides AB and CD of a parallelogram ABCD are P and Q respectively. If AQ and CP divide the diagonal BD into three parts BX, XY and YD, then which one of the following is correct ?
View SolutionP and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionIn figure, P is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. Prove that AD = 2CD. ltBrgt
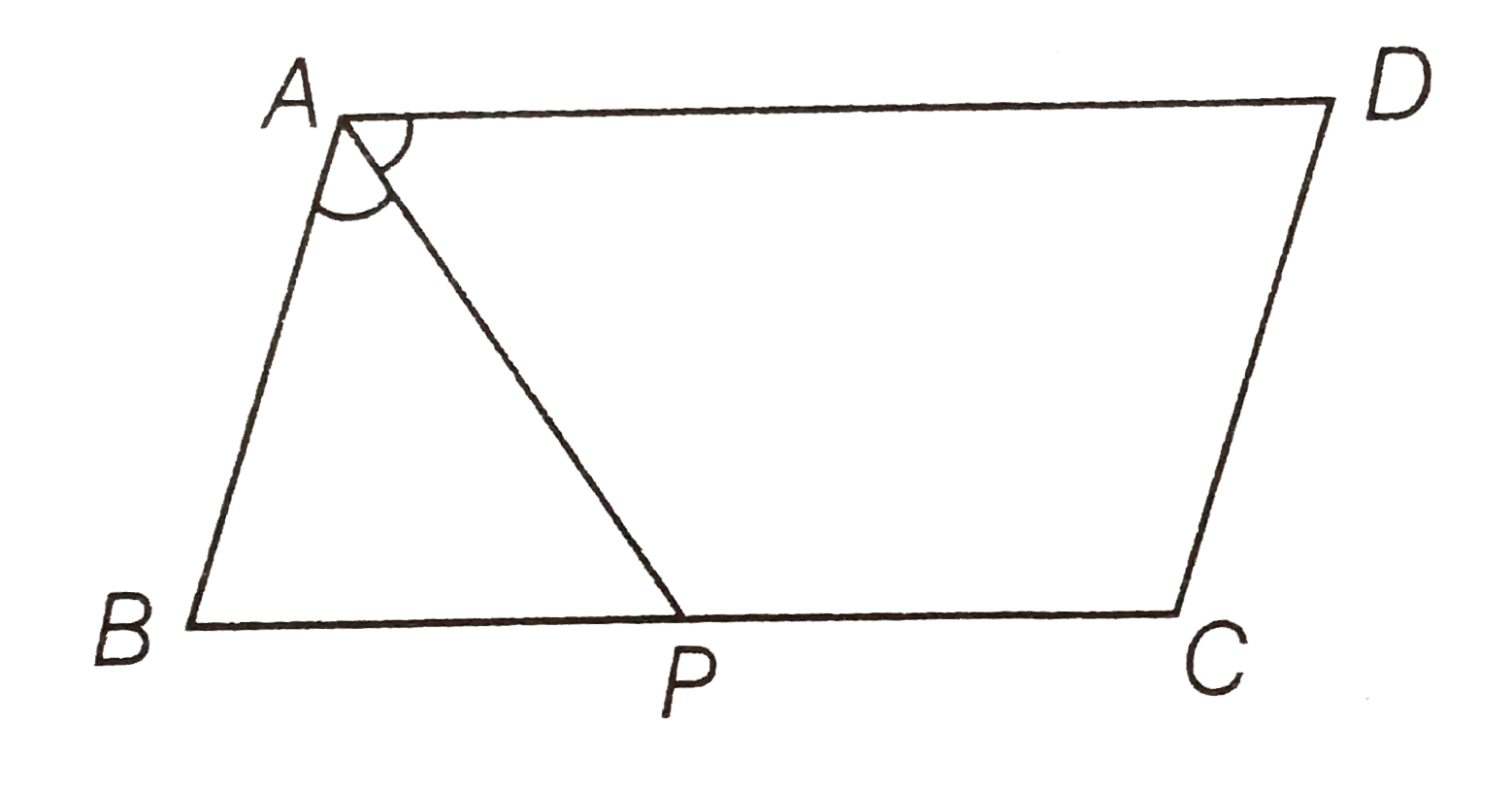 View Solution
View Solution

