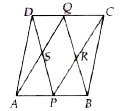
P and Q are the mid-point of the oposite sides AB and CD of a parallelogram ABCD. AQ interects DP at S and BQ interects CP at R. Show that PQRS is a parallelogram.

Video Solution

Text Solution

Verified by Experts

Given: A parallelogram ABCD in which P and Q are the mid-points of the sides AB and CD respectively. AQ intersects DP at S and BQ interects CP respectively. AQ intersects DP at S and BQ intersects Cp at R.
To prove: PRQS is a parallelogram.
$Proof: D C || A B (because opposite sides of a parallelogram are parallel)$
$\Rightarrow A P || Q C$
$D C || A B (∵ opposite sides of a parallelogram are equal)$
$\Rightarrow \frac{1}{2} D C = \frac{1}{2} A B$
$\Rightarrow Q C = A P (∵ P is mid-point of AB and Q is mid-points of CD)$
$\Rightarrow A P C Q is a parallelogram. (∵ A P || Q C and Q C = A P)$
$∴ A Q || P C (∵ opposite sides of a parallelogram are parallel)$
$\Rightarrow S Q || P R$
$Similarly, S P || Q R$
$∴$ Quadrilateral PQRS is a parallelogram.

Updated on:21/07/2023

X and Y are the mid-points of the opposite sides AB and DC of a parallelogram ABCD. Then $□ A X C Y$ is a ?
ATrapezium
BKite
CRhombus
DParallelogram
If P and Q are the middle points of the sides BC and CD of the parallelogram ABCD, then AP+AQ is equal to
AAC
B $\frac{1}{2} A C$
C $\frac{2}{3} A C$
D $\frac{3}{2} A C$
In the given figure, M is the mid-point of the side CD of the parallelogram ABCD. What is ON:OB?

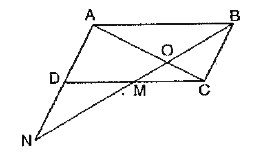A $3 : 2$
B $2 : 1$
C $3 : 1$
D $5 : 2$