Consider a perfectly conducting uniform disc of mass m and radius 'a' hinged in a vertical plane from its centre and free to rotate with respect to hinge. A resistance R is connected between centre of the disc annd periphery by using two sliding contacts C1 & C2. A long non -conducting massless string is wrapped around the disk, whose another end is attached with a block of mass m. There exists a uniform horizontal magnetic field B, whose arrangement is shown in figure.

Given system is released from rest at t=0. Assume friction between string and disc is sufficient so that there is no slipping between them let at any instant t, velocity of block is v, angular velocity of the disc is ω and current in resistance is i
Just after t=0 the acceleration of block is:
g
g2
2g3
g5
The correct Answer is:C
Writing energy equation
mgv=mvdvdt+Iωdωdt+i2R………..i
v=aω
dvdt=adωdt
i=Bωa22R=Bva2R………ii
From equation i and ii
3m2dvdt=mg−B2a26mRv
v=4mgRB2a2(1−e−(B2a26mr)t)
dvdt=2g3e−B2a26mRt

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
Knowledge Check
Consider a perfectly conducting uniform disc of mass m and radius 'a' hinged in a vertical plane from its centre and free to rotate with respect to hinge. A resistance R is connected between centre of the disc annd periphery by using two sliding contacts C1 & C2. A long non -conducting massless string is wrapped around the disk, whose another end is attached with a block of mass m. There exists a uniform horizontal magnetic field B, whose arrangement is shown in figure.

Given system is released from rest at t=0. Assume friction between string and disc is sufficient so that there is no slipping between them let at any instant t, velocity of block is v, angular velocity of the disc is ω and current in resitance is i
Find the terminal speed of the block of mass m (Terminal speed = constant speed attained by the block after very long time)AmgRB2a2B2mgRB2a2C3mgRB2a2D4mgRB2a2A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
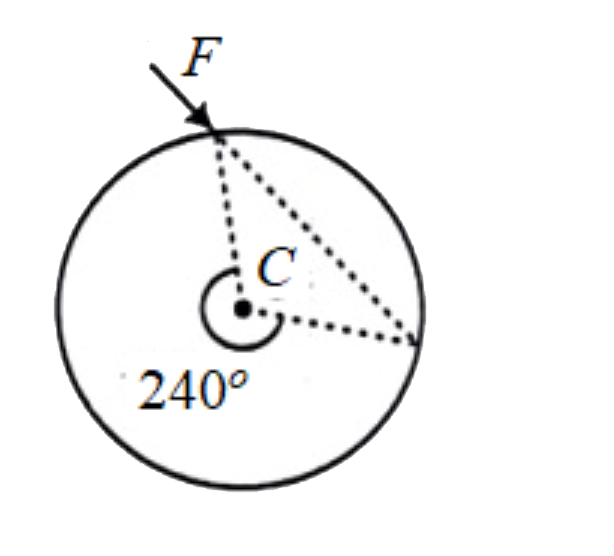 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRA force F acts tangentially on a part of a uniform disc of mass 'm' and radius 'R' hinged at point O. The force exerted by hinge on the portion of disc initially.
 A(4−ππ)FB4FπCF(π−2π)DF2
A(4−ππ)FB4FπCF(π−2π)DF2
Two equal and opposite forces F are allplied tangentially to a uniform disc of mass M and radius R . If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :
View SolutionTwo equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

View SolutionA force F acts tangentially on a part of a uniform disc of mass 'm' and radius 'R' hinged at point O. The force exerted by hinge on the portion of disc initially.

View SolutionA mass less string is wrapped around a uniform disc of mass m and radius r. The string passes over a mass less pulley and is tied to a block of mass M at its other end (see figure). The system is released from rest. Assume that the string does not slip with respect to the disc.
(a) Find the acceleration of the block for the case M=m
(b) Find Mm for which the block can accelerate upwards.
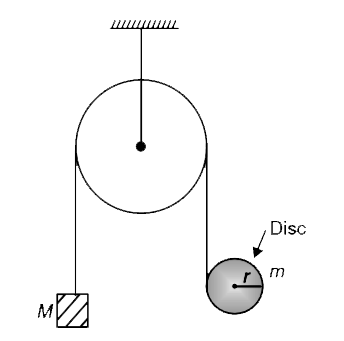
View SolutionA uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
View Solution
