The graph of the derivative f of a continuous function f is shown with f(0)=0
The graph of the derivative f of a continuous function f is shown with f(0)=0 If f(x) has local minima at x=x(1) and x=x(2),f has inflection point at x=k, number of critical points of y=f(x) is w then x(1)+x(2)-k-w is...........
If f(x) has local minima at x=x1 and x=x2,f has inflection point at x=k, number of critical points of y=f(x) is w then x1+x2−k−w is...........

Text Solution
Verified by Experts

The correct Answer is:1

[1]
x1=4,x2=8,k=3,w=4

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the graph of the function y=f(x) is as shown :
    ocr_image
    The graph of y=1/2(|f(x)|−f(x)) is

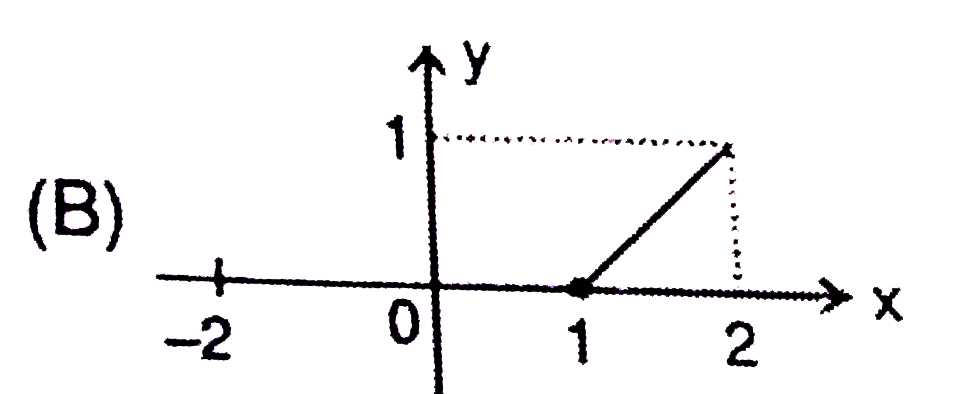    Aocr_image
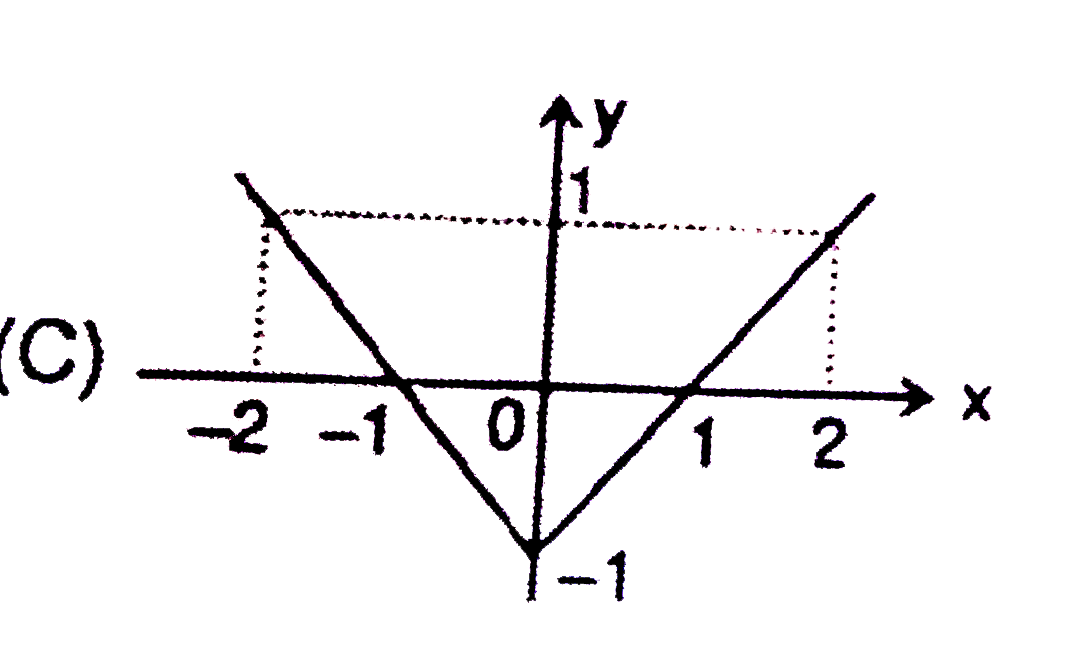    Bocr_image
    Cocr_image
    Docr_image

  • Let three degree polynomial function f(x) has local maximum at x = -1 and f(-1) = 2, f(3) = 18, f'(x) has a minima at x = 0, then :

    Athe distance between (-1,2) and (a,f(a)) where a denotes point where function has local max/min is 2√5
    Bthe function decreases from 1 to 2√5
    Cthe function increases from 1 to 2√5
    Dthe function decreases from -1 to 1

  • If f(x) is continuous in [0,2] and f(0)=f(2). Then the equation f(x)=f(x+1) has

    Ano real root in [0,2]
    Bat least one real root in [0,1]
    Cat least one real root in [0,2]
    Dat least one real root in [1,2]